Коэффициент 2 в (4.43) обусловлен тем, что ошибка возникает в двух случаях: когда значение шума больше +d и когда оно меньше -d, а р(х) -четная функция. Коэффициент 1-1/п появляется потому, что в крайнем из разрешенных значений сигнала не возникает ошибки, если величина помехи превышает d в направлении «наружу», как это показано на рис. 4.49 для момента отсчета /з. Поскольку предполагается, что все требуемые значения появляются одинаково часто, вероятность появления двух крайних значений получается равной 1/п.

Так как мощность шума Pn на входе приемника в интересующей нас полосе частот от -л/Т до п/Т составляет

n = J N,dii = N,/T,

-л/г

то с учетом (4.42) отношение мощности сигнала к мощности шума на приеме определяется равенством

Ps/Piv = dMn-l)/3iVo. Если выразить из него d и подставить его в (4.43), то получим вероятность ошибки при линейной передаче L-позиционными сигналами:

10"

10"

Q() =

У2зг

о 10 15 дБ 20

Отношение сигнал/шум PPfi =S/N-

функция, ДЛЯ которой имеются таблицы (например, в [4.51,4.53]).

Рис. 4.50. Вероятность ошибочного приема посылки при передаче в первичной полосе частот:

Кривая /-для двухпозиционного сигнала; кривая -2 - для четырехпозиционного сигнала

Вместо нее часто используется также [4.51] функция erfcZ=l-erf Z=

Уп 170

-dt. При этом Q(X)0.5 erfc(.Y/V2).

Полученная формула выражает вероятность ошибочного приема одной посылки, т. е. ошибку на одном тактовом интервале. При двоичной передаче она совпадает с вероятностью ошибки в бите. При многопозициойной передаче вероятность ошибки ib бите, зависит от вероятности ошибочного приема посылки и от применяемого кодирования (см. разд. 4.1.6). Поэтому в дальнейшем для многопозиционных сигналов указывается вероятность ошибочного приема посылки. Ее зависимость от отношения сигнал/шум для двухпозиционных и четырехпозиционных сигналов показала на рис. 4.50.

Часто, однако, представляет интерес не только вероятность ошибочного приема посылки при заданном отношении сигнал/шум, но и, наоборот, отношение сигнал/шум, при котором обеспечен прием с заданной вероятностью ошибки. Для этого случая получены простые и обычно достаточные по точности приближенные формулы [4.51, С.933].

4.5.2. ВЕРОЯТНОСТЬ ОШИВКИ С УЧЕТОМ ЛИНЕЙНЫХ ИСКАЖЕНИИ

При расчете вероятности ошибки в рамках модели помех до сих пор учитывалось лишь влияние аддитивного плума. Чтобы рассчитать вероятность ошибки во всей системе передачи, необходимо учесть влияние и всех других мешающих факторов, имеющихся в канале связи. Особенно зажны линейные искажения, которые, как было отмечено в разд. 5.2, вызывают межсимвольную интерференцию. Она ведет к повышению вероятности ошибки, так как даже при отсутствии шума сигнал в точках отсчета не принимает требуемых значений, и, следовательно, уже более малое значение шума, чем то, что соответствует разности между требуемым значением и пороговым уровнем, может вести к ошибке.

Так же, как и шум, межсимвольную интерференцию следует рассматривать как случайный процесс. Однако для нее не удается построить столь же простую вероятностную модель, как для шума; характеризующее ее распределение вероятностей должно быть найдено с учетом свойств исследуемого канала связи и метода передачи. Как правило, распределение вероятностей, описывающее меж--символьную интерференцию, не может быть приближенно заменено распределением Гаусса. На рис. 4.51 в качестве примера показано распределение искажений, вызванных межсимвольной интерференцией, для случая, когда двухпозиционный парциально кодированный сигнал передается по каналу с линейно возрастающей величиной ГВЗ.

Трудности точного анализа влияния межсимвольной интерференции на вероятность ошибки послужили стимулом к разработке весьма разнообразных приближенных методов. Первая мысль, которая напрашивается, - рассчитать вклад в вероятность ошибки k

отсчетов, соседних с интересующим нас импульсом, для каждой возможной комбинации k значений. При п уровнях передачи возможны комбинаций соседних импульсов. Нижней границей для быстро уменьшающихся передаваемых импульсов является приблизительно значение Л---.10, для практических каналов k часто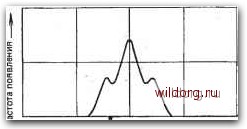

= -1 О

Отклонение от требуемого значения -

Рис. 4.51. Частота появления отклонений от требуемого значения для парциально кодированных импульсов класса 4 при линейном росте ГВЗ в полосе Найквиста с коэффициентом т/Г=0,9

должно выбираться существенно большим. Хотя объем вычислений можно уменьшить за счет «дискретизации» функции распределения, т. е. аппрокеимации плотности вероятности ступенчатой функцией [4.54], он всегда остается все же очень значительным; с ростом k объем вычислений увеличивается столь быстро, что этот способ едва ли реализуем даже и на современных вычислительных машинах. Поэтому он имеет практическое значение в основном для оценки качества приближенных методов.

Существенное уменьшение объема вычислений достигается в том случае, если ограничиться расчетом вероятности ошибки для наихудшего случая. Для этого определяется наиболее неблагоприятная последовательность k битов и рассчитывается соответствующая вероятность ошибки. Получаемая в данном случае информация для оценки системы передачи, однако, довольно мала; прежде всего, не имеет смысла сравнивать на ее основе различные методы передачи, так как никоим образом не гарантируется, что соотношение между оценкой вероятности ошибки для наихудшего случая и ее точным значением всегда одинаково. Это справедливо и для метода расчета, основанного на границе Чернова [4.55, 4.56], хотя благодаря оценке верхней границы вероятности ошибки он дает лучший результат, чем простой расчет по наихудшей последовательности данных. При этом методе, в частности, отпадает необходимость в сложном определении наихудшей комбинации передаваемых данных; можно указать разумную вероятность ошибки и для таких форм импульсов, при которых переходный процесс затухает столь медленно, что ряд, описывающий межсимвольную интерференцию, не сходится. Типичная форма импульса, при которой имеет место такой случай, - это импульс вида sin xlX, для которого произволь-172