(см. разд. 4.1.3; методы передачи в первичной полосе частот, напротив, зависят от соответствующего канала связи - кабеля или воздушной линии).

В последующих разделах рассматриваются методы передачи в первичной полосе частот, различные методы передачи с помощью модулированных сигналов, способы синхронизации и восстановления несущего колебания, а также ожидаемые при различных ме-Т(Одах передачи вероятности ошибок.

Однако прежде чем переходить к описанию перечисленных методов, целесообразно привести некоторые основополагающие све-;1ения о передаче данных.

4.1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПЕРЕДАЧИ ДАННЫХ

Один из ооновных вопросов, касающихся передачи данных с заданной скоростью, - это вопрос о распределении энергии по спектру при том или ином методе передачи.

При передаче первичных сигналов по непупинизированному кабелю полоса пропускания практически неограничена, лишь затухание увеличивается с возрастанием частоты (см. разд. 3.1.2). В этом случае,, в первую очередь, важно, не в какой полосе частот распределена основная часть энергии, а как велика та часть энергии, которая из-за переходных помех попадает на соседние пары жил в полосе частот другой системы, использующей этот же кабель.

: Передача данных с помощью первичных сигналов по пупини-зированным кабелям, а также с применением модулированных сигналов по ВЧ трактам осуществляется в ограниченной полосе частот. При этом метод передачи должен быть выбран таким образом, чтобы при надлежащей скорости передачи существенная часть энергии сигнала попадала в полосу пропускания канала связи. Во многих случаях очень важен также вопрос о скорости передачи в расчете на единицу полосы частот при том или ином методе передачи.

4.1.1. СИГНАЛЫ и ОПЕКТРЫ

Для понимания последующего изложения, прежде всего, нужно показать взаимосвязь между сигналом, заданным во временной области как функция времени g(t) и его спектром G(cu), относящимся к частотной области.

Сигнал g(t) и его спектр G(cu) связаны преобразованием Фурье [4.1, 4.2, 3*, 6*]:

Спектр G(co) является комплексным и может быть записан S виде

GH = G(a))le<«>, (4.2)

где G(co) - амплитудный спектр; ф(сй) - фазовый спектр, У вещественных сигналов g(t) компоненты спектра для положительных и соответствующих отрицательных частот являются комплексно сопряженными по отношению друг к другу:

G( (o) = G*(co). (4.3)

Если задан спектр сигнала G(cd), то с помощью преобразования, обратного (4.1), получается сам сигнал

Я(0 = JG(co)e"*dco.

(4.4)

В качестве примера рассмотрим прямоугольный импульс с амплитудой А и длительностью Т, изображенный на рис. 4.1. Согласно (4.1) получаем т/2

G(a,) = е е-"*а/ = ЛГЙ1?. J Та/2

-Г/2

Рис. 4.1. Характеристики прямоугольного импульса длительностью Т: а) временная диаграмма импульса £(4); б) спектр G(f) и его модуль \ G(if) (спектр показан только для положительных частот, в области отрицательных частот ои располагается симметрично относительно оси ординат)

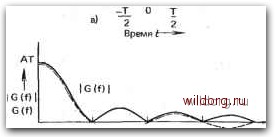Т G(f) т т

Частота /

В дальнейшем, если речь идет о случайных сигналах, используется также понятие спектральной плотности мощности [4.1]. Здесь она подробно ие определяется, поскольку для сигналов в виде отдельных импульсов (которые в большинстве случаев рассматриваются в книге) спектральная плотность соответствует квадрату их амплитудного спектра. В остальных случаях сделаны ссылки иа соответствующую литературу.

или с учетом <о=2я/ С(а>)=»ЛГ

я Г/

Спектр этого прямоугольного импульса, показанный на рис. 4.1 лишь для положительных частот, занимает все частоты от -оо до оо. Для передачи такого импульса теоретически была бы необходима бесконечная полоса частот.

4,1.2. ряд фурье

Приведенный в последнем примере анализ можно распространить на любую последовательность периодически повторяемых прямоугольных импульсов такого же вида. Периодическая последовательность прямоугольных импульсов, как известно, может быть разложена в ряд Фурье, т. е. в сумму синусоидальных колебаний.

В общем случае разложение некоторой периодической функции f(t) в ряд Фурье имеет вид

f (0 = -Y+J] [On cosпюр-I-&„sinnCDpf],

где Юр - частота основного колебания или первой гармоники сигнала f(t), определяемая его периодом Го: сор=2я/Го. Постоянные коэффициенты и Ьп выражаются через функцию f(t):

То/2 Г„/2

J f (t) COS п (Ир tdt; Ь„=» J f (t) sin neap tdt.

[To .

-Г./2 -Г./2

где n - целые числа 1, 2, ...

Коэффициент Оо выражает постоянную составляющую

Т„/2

" f{t)dt.

То .

-Тв/2

Ряд Фурье можно представить также в виде

где постоянные амплитуды Сп= V ап+Ьп, а фазы <Рп= = arctg(b„/a„).

Если рассмотреть теперь в качестве примера периодическую последовательность прямоугольных импульсов длительностью Г