витом. Каждому символу Xi из некоторого алфавита можно приписать определенную вероятность р {xi) его появления.

Появление определенного символа xi можно рассматривать как событие Xi. Множества Х= {xi, х,..., Хп} из >N возможных взаимоисключающих друг друга событий и соответствующих им вероятностей рх={р(х{), p{x2),...-,p(xn)} образуют поле событий {X, Рх), причем справедливы следующие соотношения:

Р()>0; (2-3)

Если каждому событию Xi приведено в соответствие определенное (конечное) числовое значение tf{xi), то f{X) называется случайной величиной с математическим ожиданием

E{f{X)]=p{x,)f{x{). (2.4)

Каждому событию Xi можно привести в соответствие числовое значение I{Xi), с помощью которого может быть измерена информация, заключающаяся в появлении события Xi. С этой точки зрения получение информации связано с устранением ранее существующей неопределенности. Связанная с событием л:,- информация! или мера устраняемой им неопределенности тем больше, чем более неожиданным было событие Xi, т. е. чем меньше вероятность р(Хг). Следовательно, I{Xi) =f [р(д;,-)] является такой функцией F вероятности р{Хг), значения которой тем больше, чем меньше p(Xi).

Совместное появление двух взаимно независимых событий, Xi и Xk, из X с вероятностями p(xi) и р{х), например, как пары в последовательности событий, но правилам теории вероятностей имеет вероятность p{Xi, Xk) - р {Xi) р (Хк) Тогда информация, заключающаяся в паре событий, К (xt, x„) = F Ip (Xi, %) = F Ip (xt) p (%)],

И так как xi и х взаимно независимы, то разумно потребовать, чтобы количество информации, связанной с парой событий, Xi, Xk, было равно сумме количеств информации, содержащихся в отдельных событиях: /{Xt, x„) = l{xt)-hlix,,), т. е.

Р [Р iXi) р (%)] = /= [р (Xi)] + FIP (%)].

Последнее выражение представляет собой функциональное уравнение логарифмической функции. Отсюда при использовании логарифма по основанию 2 с некоторым свободным параметром К получается

fixiJ = Khg,p{xt). (2.5)

2* . • 35

. Параметр К определяется исходя из того, что решение об одном из двух независимых равновероятных событий содержит информацию в 1 бит. Поскольку каждое из двух таких событий имеет вероятность р=0,5, то согласно (2.5) получается l=/<log20,5 или ./С=-1. Отсюда

/ix,)=-logp{xi) = \og-j-. (2.6)

Выражение (2.6) можно рассматривать как определение поня-•тия информации [2.П]. Информация, согласно (2.6), тем больше, чем менее вероятно появление соответствующего события. Наоборот, событие, которое можно предсказать с достоверностью (р=1), -не несет информации. •

Информация I{Xi) есть случайная величина. Поэтому можно в соответствии с? (2.4) определить математическое ожидание инфор-.мации в поле событий:

.Я-£[/(Х)] = р(х,)= p(x,)log,-1-. (2.7)

Это математическое ожидание, или средняя информация, называется энтропией множества событий Х=.{х{}. При этом для

р(Хг)=0

Если все N событий имеют одинаковую вероятность, то p(Xi)=p=\IN и из (2.7)

Я = = Я„ = log, = log, Л. (2.8)

В этом случае энтропия максимальна и в общем справедливо

Я(X)<logгiV = Яo(X). (2.9)

Отклонение энтропии Н(Х) от ее максимального значения Но(Х) называют избыточностью:

R(X)H{X)-H{X). (2.10)

«Относительная» избыточность

г(Х)=1-Я.(Х)/Яо(Х). (2.11)

Для передачи данных особенно важен двоичный источник, ал-фавит которого состоит только из символов О и 1: X-{G\ 1}. Если символам приписаны вероятности р{0)=р и р(1) = 1-р, то согласно i(2.7)

Я(Х) = S(p) = plog, у-f(l-p)log2-j-. (2.12)

i36 . .

По предложению Э. Бергера [2.12] функцию S{p) назЫйают также функцией Шеннона. Ее вид показан на рис. 2.5. Функция S(p) обращается в единицу для р=0,5 и в нуль для р==0, р=1. В общем случае, если в выражении (2.7) не ограничиваться двоичным алфавитом, события со «средней» -вероятностью дают относительно большой вклад в энтропию Н{Х), в то время как частые события из-за их малой информативности и редкие события из-за их ма-ловероятности вносят в энтропию лишь малую долю.

Название «энтропия» для математического ожидания информации в поле событий -первоначально было введено К. Э. Шенноном [2.4, 2.5] только на основе формальной аналогии с результатами Л. Больцмана, каса-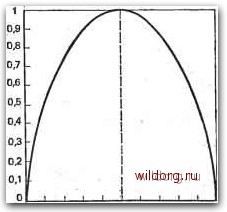

0 0,1 0,2 0,3 0,4 0,В 0,6 0,7 0,8 0,9 1

Рис. 2.5. Функция Шеннона S(p)

ющимися термодинамической энтропии. Однако, кроме этого, существует и физическая связь между обоими понятиями энтропии 12.11, 2.14-2.17].

2.3.2. ПЕРЕДАННАЯ ИНФОРМАЦИЯ. ПРОПУСКНАЯ СПОСОБНОСТЬ КАНАЛА СВЯЗИ

В разд. 2.3.1 было рассмотрено единственное поле событий Рх), а именно алфавит источника, из которого путем операции выбора формируется последовательность символов, несущая ин-•формацию. Эта информация должна быть передана по каналу к получателю (см. рис. 2.1). При этом предполагается, что получателю известен алфавит источника. Поступающая к получателю информация также образует некоторое поле событий {Y. ру), которое по объему может отличаться от поля источника.

Пусть некоторый символ Xi с вероятностью р{Хг), посланный источником, после передачи по каналу связи появляется у получателя как символ г/ь с условной вероятностью р(уп1Хг). Эта вероятность называется условной, потому что она характеризует появление yf при условии, ЧТО быЛ ПОСЛЗН символ Хг.