Т а б л и ц а 6.6

Параметры коммутационных схем и нагрузки

Структура коммутационной схемы . • . .

Число входящих подгрупп или очередей " •

Число исходящих линий (вызовов) - j

Число ступеней

Доступность :

постоянная и полная

постоянная, но не полная, например смешивающее включение

зависящая от нагрузки, иа холостом ходу - полная, например, как в

схеме соединительных линий на рис. 6.11

зависящая от нагрузки, неполная также и на холостом ходу

Число мест ожидания

яет мест ожидания - чистая система с потерями

- ограниченное число мест - комбинированная система с ожиданием и с потерями

неограниченное число мест - чистая система с ожиданием • • ,

Дисциплина обслуживания

Дисциплина внутри очереди-

с учетом или без учета ожидаемой длительности занятия с различными приоритетами или без различных приоритетов приоритеты - прерывающие или «епрерывающие, вытесняющие или невытесняющие

обслуживание при одинаковых приоритетах и без учета ожидаемой длительности занятия, например

в порядке поступления (пришел первым - обслужен первым) в случайном порядке

в порядке, обратном поступлению (пришел последним - обслужен первым)

Дисциплина очередей (межочередйая дисциплина) Нагрузка

Интервалы между вызовами

не зависимые от состояния, например распределенные экспоненциально зависимые от состояния, например от числа свободных выводов

Длительность занятия, например, постоянная

экспоненциально распределенная . • -

Существуют одноступенчатые (однозвенные) коммутационные схемы, которые состоят из расположенных рядом друг с другом коммутаторов и дополнительной кроссовой схемы иа выходе - смешивающей схемы (рис. 6.10) [6.14]. Она необходима в том случае, когда общее число выходов коммутатора больше числа выводов, однако в первую очередь она служит для. повышения

9-41 2,33,

пропускной способности коммутационной схемы: пики нагрузки в группах вводов в общем случае не совпадают по времени, поэтому за счет смещ-ивающего включения достигается выравнивание нагрузки.

Входы

Выходы

-г--т. -Г--Г.

~7.-

• m I tT

2 •••

Сокращенное обозначение

Рис. 6.9. Многократный соединитель

Многоступенчатые (многозвенные) коммутационные схемы состоят из коммутаторов, включенных друг за другом. При этом, вообще говоря, общее число выходов одной ступени равно числу промежуточных линий, ведущих к следующей ступени, как показано на рис. 6.11. Так как иска-

..руппь. вжодьГ""смещивающее Выводыние пуТИ распространяется На ВСЮ

Выходы

m 1

включение

-4 -5

Рис. 6.10. схемы

Пример

Входящие подгруппы

коммутационную схему, то промежуточные линии (в отличие от исходящих, которые ведут к другой коммутационной схеме) занимаются только тогда, когда путь через следующий коммутатор свободен. Как и одноступенчатые схемы, промежуточные соединительные линии могут быть допол-смешивающеи нены смешивающей схемой.

Отходящие пучки

Ь Z

Сокращенное обозначение

Рис. 6.11. Схема промежуточных линий для соединения входящих подгрупп (г) с исходящими пучка-жи (6)

с точки зрения теории телетрафика важнейшим параметром, характеризующим структуру коммутационной схемы, является" доступность, определяемая как число k выводов, которые могут быть проверены со стороны одного ввода на их занятость. Доступность называется полной, а доступная в этом смысле группа линий называется полнодоступной, если количество доступных выводов равно общему числу выводов в этой группе. Примером может служить случай схемы, состоящей лишь из одного коммутатора. Одноступенчатая схема со смешивающим включением имеет ограниченную доступность, так как с самого начала определенные выводы еедоступмы. Доступность при этом постоянна. У многоступенчатых схем доступность также часто ограничена. Она зависит от внутренней блокировки, которая состоит в том, что из-за временной занятости промежуточных линий определенное число выводов может оказаться недоступным (рис. 6.12). Доступность у Многоступенчатых схем в этом Случае является переменной, т. е. зависит от занятости и тем самым от нагрузкИ. Она оказывается, наибольшей, если нет занятости (холостой ход).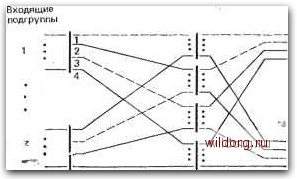

Отходящие пучки

1

Рис. 6.12. Двухступенчатая коммутационная схема с доступностью на холостом; ходу Л=4 (по четыре промежуточных линии) и мгновенной доступностью исходящего пучка 1 для входящей подгруппы 1 (свободны только промежуточные линии 2 и 4 k=2:

- свободные линии.

занятые линии

Состояние занятости коммутационной схемы при полной доступности в достаточной степени характеризуется числом занятых выводов. Напротив, при ограниченной доступности возможность, закрепить определенную группу вводов за некоторым выводом зат висит не только от числа занятых выводов, но и от того какие.иаз них заняты, а у схем с промежуточными линиями также и от.-то-го, какие промежуточные линии заняты. Поэтому количество- разт-личных состояний занятости в этом случае существенно больш-е..

Структура коммутационной схемы определяет и возможности-

9* 23s