пользовании импульсов класса 4 по методу парциальных отсчетов. Если парциально кодированный импульс имеет вид

g{t) = 2n

а его преобразование Гильберта

ТО сигнал на выходе, демодулятора (см. разд. 4.3.1.2) согласно (4.21) имеет вид [4.49]

gs it)--~-[sin Ф cos е - sin е (1 + cos Ф)],

ф2 - я

где Ф-ntlT - фаза тактов; 6 - фаза несущей. Искажения в канале связи не учитываются.

Данное соотнощение выражает связь между процессами уста-

i несущей о

: 1,оог 7

Фаза несущей 1,00Г -"

0,80

0,60

0,40

0,20 >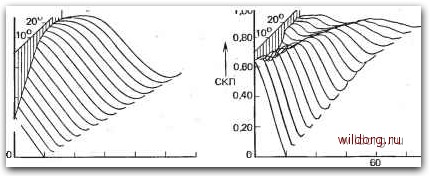

-20 О 20 40 Фаза тактов,град

60 80 100

-20 О 20 40 б) фаза тактов, град

80 100

Рис. 4.44. Влияние погрешностей в фазах тактов и несущего колебания на средпеквадратическую погрешность (СКП) при амплитудной модуляции с одной боковой полосой (с применением парциально кодированных импульсов класса 4):

а) для трехпозициоиного принимаемого сигнала; б) для семипозиционного принимаемого сигнала

Среднеквадратическая погрешность (см. разд. 5.1.2) определяется при этом суммой квадратов отклонений отсчетов принятого сигнала от их идеальных значений. Если появляется погрешность, превышающая половину разности двух отсчетных значений, отсчет определяется неверно. Поэтому при отклонении от точки минимума среднеквадратическая погрешность не возрастает постоянно. Вернее, ее изменение уже несущественно, если межсимвольная интерференция, обусловленная погрешностями фаз тактов и несущей, так велика, что появляются ошибки в решении.

новки фаз несущей и тактов. Для заданной погрешности в фазе несущей е существует некоторая оптимальная фаза тактов, при которой возникающая погрешность минимальна. Чтобы пояснить эту взаимосвязь, на рис. 4.44 представлены графики среднеквадрати-ческой погрешности (СКП) трехуровневого и семиуровневого парциально кодированных сигналов в зависимости от фаз тактов и несущей. На обоих графиках СКП отчетливо различима «впадина», проходящая примерно вдоль плоскости, которая для наглядности выбрана правой границей изображенной области. Эти графики необходимо принимать во внимание при регулировке фаз тактов и несущей, чтобы достичь возможно более точной их установки.

Практическая реализация регулирования фаз тактов и несущей сильно зависит от чувствительности выбранного метода передачи. В то время как при нечувствительных методах в соответствующих условиях можно использовать для демодуляции в качестве опорной фазы фазу передаваемого пилот-сигнала (пилот-сигнал при этом целесообразно расположить в середине полосы частот, что, например, легко осуществить при КАМ), для более чувствительных методов должен быть предусмотрен сдвиг между фазой пилот-сигнала и фазой демодулированной несущей, жестко зависящей от канала связи. В порядке дальнейшей коррекции этот фазовый сдвиг оптимизируется в процессе передачи или часть регулировки фазы выполняется адаптивным корректором (см. разд. 5.3.2). При методах передачи импульсами многопозиционного кода фаза несущей должна быть отрегулирована очень точно [4.49], что видно и из сравнения рис. 4.44а и б.

Чувствительность систем с AM, ОБП, ЧПБП и КАМ к погрешностям фазы несущей характеризуют графики, показанные на рис. 4.30, 4.45 и 4.46. Они построены в предположении, что вероятность ошибки в бите при отсутствии погрешности фазы несущей для определенного отношения сигнал/шум во всех случаях одияа-

10"

10~-

10"

о 10"

Рис. 4.45. Вероятность ошибки в бите при амплитудной модуляции с одной боковой полосой (с применением парциально кодированных импульсов класса 4) в зависимости от погрешности в фазе несущего колебания. Помехи - белый шум в полосе Найквиста. Отношение сигнал/шум 18,1 дБ

RIO"

5 10 15

Погрешность в фазе несущей, град-

кша. Самой благоприятной при этом оказывается квадратурная модуляция.

По фазомодулированному сигналу данных фаза несущей может быть восстановлена лишь с точностью до величины, кратной минимальному характеристическому значению фазы сигнала, так как

регулировка фазы несущей не

ю

5 10 15

Погрешность в фазе несущей, град-

должна зависеть от переходов фазы сигнала между точками отсчета, обусловленных модуляцией. Эта фазовая погрешность, которая, если не принимать во внимание помехи, остается постоянной в течение передачи, несущественна в системах с фазоразностной модуляцией, поскольку на приеме

Рис. 4.46. Вероятность ошибки в бите при квадратурной амплитудной модуляции в зависимости от фазы несущего колебания. Помехи - белый шум в полосе Найквиста:

кривая 1 - для парциально кодированных импульсов класса 4 при отношении сигнал/шум 18,1 дБ; кривая 2 - для импульсов с коэффициентом сглаживания спектра 0<;г1 ппи отношении сигнял/шум 16 дБ

определяется разность фаз и поэтому абсолютная фаза несущей в процессе восстановления информации не участвует.

В системах с обычной фазовой модуляцией, наоборот, знание абсолютной фазы несущей в месте приема обязательно, так как информация содержится непосредственно в фазе сигнала по отношению к несущей. В этих случаях фазовую погрешность, не поддающуюся указанной выше регулировке, необходимо выделять и корректировать отдельно. Последнее осуществляется путем обработки специальной синхронизирующей последовательности, которая предварительно вводится в каждый блок данных [4.50].

4.5. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ НАЛИЧИИ ПОМЕХ

Источниками помех при передаче данных являются, например, другие каналы связи или случайным образом меняющиеся переходные сопротивления контактов (см. разд. 3.2.2.7). Влияние на передачу данных большого числа различных случайных помех, действующих в реальных каналах связи, можно сравнительно просто оценить, если в качестве модели помех принять белый шум, т. е. шум, имеющий постоянную спектральную плотность мощности Ло