системах , с квадратурной амплитудной модуляцией (см. разд. 4.3.1.3). Как показано иа рис. 4.8, выбросы такого сигнала уменьшаются тем сильнее, чем больше коэффициент сглаживания, т. е. «чем шире занимаемая полоса частот.. Благодаря этому характеристические значения импульса становятся менее чув.ствительны-ми к смеихению во времени моментов отсчета, поскольку влияние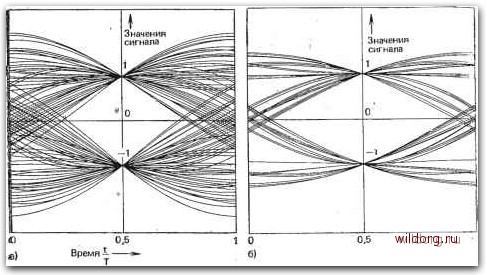

Время -

-да) Л10

Рис. 4.9. Глазковая диаграмма при различных коэффициентах сглаживания г, полученная методом моделирования с использованием квазислучайнон после-дрвательности длиной 63 бита и учетом десяти начальных и десяти конечных колебаний: а) /-=0,1; б) 1Г=0,5 в) г=1,0

соседних импульсов меньше. Это видно из глазковой диаграммы (рис. 4.9) как по горизонтальной ширине «глазка» для импульсов с /- = 0,1 (рис. 4.9а) и г = 0,5 (рис. 4.96), так и по более быстро возрастающим отклонениям от характеристических значений в вер-

тикальном направлении при отклонениях от оптимальной точки отсчета.

При т= 1 импульс содержит дополнительную нулевую точку между моментами отсчета, так что не только значения сигнала в точках отсчета, но и мгновенные значения в середине между этими точками могут быть определены без искажений. Кроме того, за время t=±T/2 максимальное значение d главного импульса падает наполовину, до значения d/2 (см. рис. 4.8).

Этот импульсный сигнал удовлетворяет второму условию Найквиста [4.6], которое требует, чтобы вне интервала -ГГ (с центром в точке отсчета) имели место нули при Ь=±пТ, где и= =2, 3, а значения сигнала при удалении на ±Г/2 от точки отсчета составляли половину максимального значения.

Таким образом, с помощью этого импульса в приемнике можно определить первоначальную длительность переданного импульса, т. е. избежать краевых искажений, что видно и из глазковой диаграммы на рис. 4.9б. Диаграмма указывает также на некритичность к отклонениям от оптимальных моментов отсчета.

Для передачи двоичных сигналов со скоростью v=llT в полосе частот f= {1/Т+г/Т) /2 удельная скорость передачи, т. е. скорость передачи в расчете на единицу полосы частот, составляет, бит-с~7Гц,

0 = 2/(1+7-). ... :

Так как коэффициент сглаживания г лежит между нулем и единицей, удельная скорость передачи здесь меньше 2 - это теоретический максимум, достигаемый только для импульса вида sin х/х.

Малые коэффициенты сглаживания, обеспечивающие высокую удельную скорость передачи, из-за требований к точности моментов отсчета трудно реализуемы. Из литературы [4.7] известны, например, системы с коэффициентом сглаживания 0,16, которому соответствует удельная скорость передачи 1,72 бит-с/Гн. Сигналы с такими коэффициентами используются в устройствах передачи со скоростью 9600 бит/с по некоммутируемым трактам с полосой частот канала ТЧ (см. том 2, разд. 7.3).

Конечно, можно использовать импульсы другой формы, удовлетворяющие первому или второму условиям Найквиста лишь приближенно. При этом, однако, требуется более широкая полоса частот, чем для «сглаженных», как описано выше, импульсов. Примером может служить импульс, показанный на рис. 4.10 [4.8]. Как видно, практически его спектр занимает частоты до 3/Г и спадает очень быстро. Такого рода импульсы можно применять, например, для передачи в первичной полосе частот (разд. 4.2), поскольку в этом случае удельная скорость передачи не играет такой большой роли.

G(f)

-0,5

2T T Частота-s

2T 6)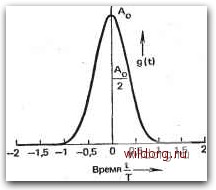

Puc. 4.10. XapaKTepiiCTHKH импульса с колоколообразным спектром G(f) [4.8]: а) спектр G{i)-e--<-f>\ б) сигнал g{t) (при tlT=±l его значение уменьшается до величины 0,01 До)

4.1,5- МЕТОДЫ ПАРЦИАЛЬНЫХ ОТСЧЕТОВ

с помощью импульсов, удовлетворяющих первому условию Найквиста, лишь в пределе можно достичь удельной скорости передачи 2 бит-с-/Гц. Для реализации этого максимального значения скорости при передаче двоичных сигналов разработан ряд -методов - двойной двоичный (дуобинарный), полидвоичный,. двойной троичный (битернарный), а также метод парциальных стсчетов [4.9-4.15]. Их можно объединить под общим названием методы парциальных отсчетов [4.15] или парциального кодирования.

Характерно, что рассматриваемые импульсы при скорости передачи l/T занимают два или более тактовых интервалов дли--тельностью Т (начальное и конечное колебания во внимание не принимаются). Ряд основных форм импульсов показан на рис. 4.11. .Подразделение на классы 1-5 предложено Кречмером [4.15], .форма импульсов класса 6 задана в [4.16]. Для реализации удельной скорости передачи 2 бит-с/Гд необходимо ограничить спектр полосой Найквиста. Тогда по теореме отсчетов импульсы однозначно определены своими отсчетами. Как ясно из рис. 4.11, каждый класс импульсов характеризуется совокупностью т коэффициентов {ki}, /=!, 2, т, через которые пропорционально несущему информацию характеристическому значению выражаются соответствующие отсчеты импульсов. Например, импульс класса 4 определяется своими отсчетами kibi = {l-bi, 0-bi, -l-bi}. При передаче двоичных символов характеристическими значениями {bi} = = {d, 0} в приведенном примере логическим состоянием 1 и 2 ставятся в соответствие импульсы {d, О, -d} и {О, О, 0}. 112