т. е. экспоненциальный фильтр уточняет отфильтрованное значение на выходе cpj, как только на вход поступает новое значение. Это уточнение невелико и становится ещ меньше для значений а, близких к 1; в этом случае появляется эффект инерционносхр Уменьшение шумовых компонентов выходного сигнала происходит за счет слабого ответствия с реальными изменениями на входе. При а, близком к нулю, величина П(, правки растет. Соответственно, фильтрация шума уменьшится, однако изменения ис ходного сигнала будут отслеживаться более точно. При а = О сигнал на въщ идентичен сигналу на входе. Влияние величины а на реакцию фильтра при скачке за шумленного входного сигнала проиллюстрировано на рис. 5.23.

Пример 5.9

Интерпретация экспоненциального фильтра как фильтра скользящего среднего

Экспоненциальный фильтр можно интерпретировать как фильтр скользящего среднего, у которого в уравнении (5.9) бесконечное число членов с коэффициентами bj и отсутствием членов с коэффициентами а. Коэффициенты bj быстро уменьшаются Д.ЛЯ более старых значений во входной последовательности. Этот результат можно получить, переписав уравнение (5.10) как

y(kh) =a-y[{k~\)h\ + {i-a)-y{kh)-

= {\-a)-y(kh) + a-{\-a)-y\(k-\)h\ + a y]fk-2)h =

= (1 - a) y{kh) + a-{i- a)-y\f,k - \)h\ + a? y[{k - 2)h\ + y[(k - 3)h] =

= (1 - a) y(kh) -H a (1 - a) • y[(k - l)h] + ... + a"-y[(k - n)h] + ...

Tnebfj = I - a,by = a - (i - a),b2 = a? (i - а)1п.д.. Так как О < a < 1, то коэффициенты для более старых значений убывают по экспоненциальному закону-Например, при а = 0.5 коэффициенты равны 0,5, 0.25, 0.125, 0.0625,а при а = 0.9 - 0.1, 0.09, 0.081, 0,072, ... Другими словами, если а стремится к 1, то фильтр имеет более долгую "память" и более эффективно сглаживает входной сигнал. Из-за экспоненциального убывания значений коэффициентов фильтр и получил свое название.

Экспоненциальный фильтр в действительности представляет собой дискретны" риант аналогового ФНЧ первого порядка с единичным статическим коэффидиен усиления (см. раздел 5.3.1) и передаточной функцией, аналогичной уравнению (S.-i,

Y(s) 1 fm 1+s-T

Постоянная времени Т равна R С либо L/R в зависимости от вида фильтра. /" ференциальное уравнение цифрового фильтра

0.5 О

AiiLitljtLtkLiJt<Lti...jiiliUL<jLl<..

а = 0

1.0 0.5 О

а-0.5

1.0 0.5 О

/ , 1.0.

1.0 0.5-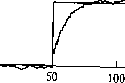

а = 0.95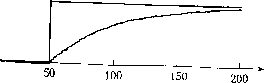

а = 0.98

Сн°:°™° -съеживает Шмененя во вдГсинГе™ « Ф-р до-У- При больших значениях а фильтр вноси; знаГгелТГо заметно подавляется. При а = О выходной сигнал фГлГтм 11

1 oji фильтра идентичен входному

При аппроксимации производной обратными разностями получщ

yit)-y(t-h) h

что является достаточно хорошим приближением для малых значений h можно упростить следующим образом

y(t) =

y{t-h)+ - -

y(t)

что идентично уравнению (5,10) при

1 -а

Поскольку было принято, что л/г мало, то аппроксимация верна, только ее. стремится к 1. В этом случае а можно определить следующим приближенным bi жением

а= 1

1 -а

В действительности точное решение дифференциального уравнения (5.П) уравнение (5.10)

1п(а)

для которого выражение (5.12) является хорошим приближением при мачых ниях h/T. с-

Реакция фильтра на скачок входного сигнала (рис. 5.23) иллюстрК между а и Г. В течение интервала, равного одной постоянной времени . выходе достигает 63 % от величины окончательного значения: при а - пая времени Гравна примерно 20 интервалам выборки, а при а - 0.9» тервалов.

Пример5.10

Программа, реализующая экспоненциальный фильтр

Цифровой экспоненциальный фильтр [уравнение (5.10)] -" р,-вать программными средствами. Ниже приведен примерный вариаь мы. Функции AD input и DA outpnt используются д.чя ввода и в

--"" Переменная delta time есть интервал выборки, а

нь1."< °°ользуется для синхронизации работы программы с выборкой !ext time исполь pgg g 5

program exponential filter Jar .n signal alpha y filtered, y old: next Jime, delta time:

real; real; real;

begin

next time := 0;

while true do (* бесконечный цикл *) begin

wait until(next time); in signal := ADJnput (ch#l); y filtered := alpha*y oId + (l-alpha)*in signal; y old := y filtered; DA ontpnt (ch#2, y filtered); next time := next time + delta time; end; (* бесконечного цикла *)

end; (* exponential filter *)

5.4.3. Цифровые фильтры низкой частоты высоких порядков

Аналоговый фильтр второго порядка более эффективен для подавления высоко-филь™" компонентов, чем фильтр первого порядка (раздел 5.3.2). Цифровой анз,°РУктурой, определяемой уравнением (5.9), при и = m = 2 соответствует ьных 4) Vy второго порядка. Соединив последовательно два экспоненци-<овы.чи первого порядка, получим фильтр второго порядка с двумя одина-частотами среза

значр

yikh) = а i[( - 1)/2] + (1 - а) • у{Ш) У2{Щ -ay2[{k~\)h] + {\-a)-y{kh)

•"ой сигнал сигнала, у- - выходной сигнал первого фильтра, а 2 ~

"сключить пе™°™ Фльтра. Свойства фильтра определяются параметром а.

ледуюп.о™- 1) цифровой фильтр второго порядка можно за-- ""щем виде

/ульха;р ~ a 2)h] + (1 - а)2 . ут

"оказан на"";*™ второго порядка к сигналу, изображенному на о"- поэто Фильтр второго порядка эффективнее подавляет вы-"Точнее соотГ ожно выбрать меньшее значение а. Выходной сигнал этого етствует изменениям входного сигнала, чем у фильтра первого

Глава 5.

0.5 О

1.0 0.5 О

iilihilifMlililnlkiiiiiiLiiJiiilrthiAlli

а = 0

150 200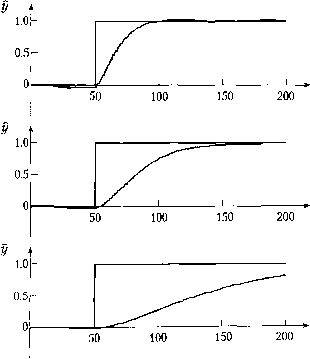

а = 0.9

а = 0.95

а = 0.98

Рис. 5.24. Влияние экспоненциального фильтра второго порядка при разных значени ях параметра а

Применение фильтров более высоких порядков [уравнение (5.9)] позволяет больше улучшить качество выходного сигнала. Платой за это является увелйЧ сложности фильтра, однако стоимость обработки данных невелика. Следует о тить, что если в аналоговых фильтрах добавление пассивных электронных к»

фильтрация

цепи фильтра означает дополнительные энергетические потери в сигнале, ""й программной реализации этой проблемы не существует.

5 4 4 Цифровые фильтры высокой частоты

jgKOTopbix случаях необходимо выделить высокочастотные компоненты сигна-

п яявные изменения. Поэтому сигнал должен быть обработан фильтром высо-ла, анепда

частоты (digital high pass filter)

y(kh) = Ay(kh) = y(kh) - y[(k - i)h

Выходной сигнал отличен от нуля только тогда, когда есть изменения во входном сигнале.

Цифровой ФВЧ можно также получить разностной аппроксимацией аналогового ФВЧ (раздел 5.3..3). Соответствующее дифференциальное уравнение аналогично уравнению (5.6)

и частоты. Разностная схема - это простой пример цифрового фильтра высокой

dy(t) ,,,dy(t)

(5.14)

где г/ - это входной сигнал, ау - выходной.

Применив к этому уравнению аппроксимацию разностями "вперед", получим цифровой ФВЧ

-Л

y(t+h) =

1-А т

у it) + y{t + h)- y(t) = a . y(t) + y(t + Л) - y(t) (5.15)

где a определяется уравнением (5.12). Дискретное уравнение фильтра можно также вывести аналитически из уравнения (5.14); в результате получим а, выраженное уравнением (5.13), значение которого должно лежать между О и 1. При а = О фильтр реализует чисто разностную схему. Следует еще раз подчеркнуть, что для применения разностной аппроксимации и уравнения (5.12) отношение h/Tдолжно быть достаточно мало.

а "ьность фильтра на высоких частотах определяется выбором значения боль " значение а приводит к большей чувствительности, которая соответствует

частоте среза для ФВЧ.

Цроиллюстрируем работу ФВЧ на нескольких примерах. На рис. 5.25 представ-*"агр°а!иГ самый скачкообразный зашумленный входной сигнал рис. 5.23. Средняя 5еря

Ра.м.ме На

сод5р "Указывает выходной сигнал чистого разностного фильтра (а = 0). Она я*.!* V °° фильтр распознает мгновенное изменение входного

0.95 пик при t = 50 становится шире, что показано на нижней диаг-

Рис. 5.26 на вход фильтра поступает синусоидальный сигнал с наложенным вы-

а бол шумом. Выходной сигнал Фв"ч сохраняет высокочастотные измене-сли* Д-нные синусоидальные колебания либо уменьшены, либо удалены. "Ходе зашумленный синусоидальный сигнал наложить скачкообразный, то на сцгн,„ ""сокочастотного фильтра появится пик, отражающий скачок во входном (Рис. 5.27).