Соответствующая цепь не проводит ток, если оба ключа А и В разомкнуть,; ес.„ разомкнут только один ключ, то цепь остается замкнутой через другой (рис.7" Так же как и элемент NOR, элемент NAND является универсальным.

и

s>-

12

А О

&

О

Рис. 7.8. Соединение ключей, схематическое обозначение и таблица истинности элемента NAND ("НЕ И")

Операции NAND и NOR называют полными, поскольку любые логические фун: ции можно выразить только через какую-нибудь одну из них. Ни один другой э мент или функция не имеют такого свойства.

На рис. 7.9 показана цепь из двух ключей: каждый ключ состоит из двух коит тов, один из которых нормально разомкнут, а другой нормально замкнут. Соотв ствующая операция называется XOR ("исключающее ИЛИ"), а ее результат опре. ляется выражением

Х = А-В- АВ

Рис. 7.9. Соединение ключей, схематическое обозначение и таблица истинности элемента XOR ("исключающее ИЛИ")

Эта цепь проводит ток в случае, только если либо А = 1, либо В = 1; если А и • имеют одно и то же значение, то на выходе X = 0. Например, такую логическую могут использовать для управления светом в помещении с помощью двух выкл» телей А и В, расположенных в разных местах. Б цифровых ЭВМ XOR-цепи при

ются для двоичного сложения.

Операция XOR позволяет определить соответствие входных разрядов (рис. 7.10): если значения совпадают, то соответствующий разряд на выходе - - че - 1. Так как применение XOR к идентичным операндам дает результат О, операцию можно использовать для проверки операндов на совпадение.

...,„„„г.,й гигнал которой X зависит только от т(

ерацию можно и----;;7к;™р;йхТаТисит только от текутее;-

Логическая п"; Juf (А, В,...), называется комбинационной четания входных сигналов и г, у. (combinatorial network)

х(0=Ли(0]

рис. 7.10. Маскирование с помощью операции XOR

Таблица, содержащая всевозможные комбинации входных сигналов и соответствующие им выходные сигналы, называется таблицей истинности (truth table). В принципе, любую переключательную сеть можно проверить с помощью таблицы „стинности. К сожалению, размер этой таблицы быстро растет с числом переменных я, поскольку число комбинаций равно 2".

Существуют различные методы упрощения булевых функций, в результате которых число связей между переменными уменьшается. Подробное обсуждение этих .методов выходит за рамки настоящей книги. При числе переменных п<6 можно использовать метод "карта Карно" (Karnaugh тар). Для более сложных выражений существуют другие методы, например метод Квайна-Маккласки (Qnine-McCluskey).

Пример 7.1

Простая комбинационная цепь

Пример простой комбинационной цепи показан нарис. 7.11.

И 112

&

>1

Простая комбинаци

02

-оответствующиеей

онная цепь логические выражения имеют вид

03 = Г1Н2

04 = 12 • 02 02 = 04 + И

Ч и!."° существует принятого во всем мире стандапта пп<, .4 "коммутирующих элементов. Символы ISO, ,Ес": "STrJtZTJ IT

„ -----J Cl принятого ъи Duv-iYi -vn.jjc Ь1 андаотя лтта гло..,.

"коммутирующихэлементов. Символы ISO, lEcTS™""™" "апример, в США широко используются по крайней .е "

"--е стандарты представления логических .эле.менто:,~

1 теории переключательных схем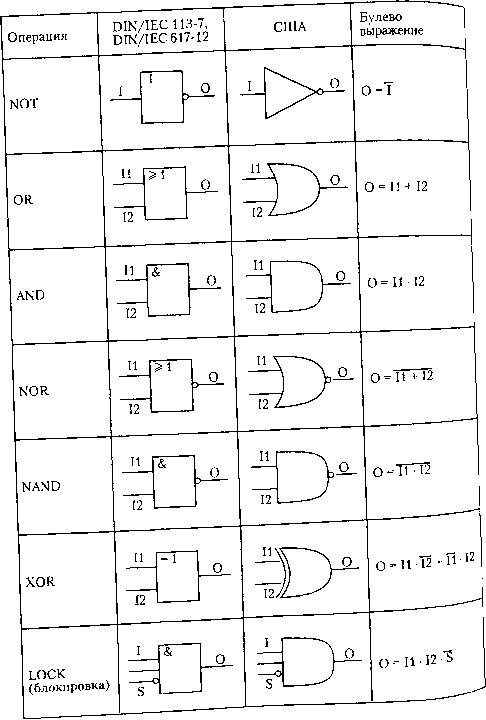

Рис. 7.12. Распространенные с

хематические обозначения логических элементов

л Элементы с двумя устойчивыми состояниями (триггеры)

7,1.4.

П сих пор описывались комбинационные сети, в которых выход X зависит толь- .[-екуЩго сочетания входных сигналов. Такие сети не имеют памяти. В после-

доват!

>льностных сетях (sequential network) можно хранить значения сигначов и со-

стояний

ле.«ентах с двумя устойчивыми состояниями {bistable), которые в русской термино-•10ГИИ называют триггерами (flip-flop; слово trigger в английском языке имеет не-ско.№ко иное значение - запускающий элемент, спусковой крючок). Выход триггера зависит не только от текущего состояния на входе, но и от предыдущего на выходе.

Простейшим элементом такого типа является SR-триггер (Set-Reset - установка-сброс). Два входа S и R могут иметь логическое значение "О" либо "1", однако им обоим нельзя принимать одно и то же значение одновременно. Выход обозначается у; обычно на интегральных схемах существует и инвертированный выход у. Если S = 1, то выход изменяется на г/ =1 (г/ = 0) и триггер переходит в состояние "установка"! Если затем вход S принимает значение "О", то триггер "помнит", что до этого он имел значение "1" и удерживает выходное значение г/ = 1. Если теперь вход R примет значение "1", то с учетом S = О триггер сбрасывается и на выходе г/= О = 1). Аналогично, как и ранее, R может вернуться к "О" и состояние г/ = О останется до тех пор, пока не появится новый сигнал S = 1. Если состояния в последовательные промежутки времени обозначить г/„ и у„+\,то эту операцию можно записать так

y„+,-R-(S + y„)

На рис. 7.13 приведены три варианта реализации SR-триггера на двух логичес-« элементах.

и использовать их позже в других операциях. Память реализуется на

>1

&

>1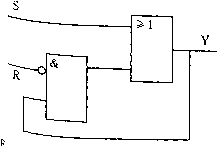

>1

3. Три варианта реализации SR-триггера и его обозначение в

стандарте IEC

Защелка {latch) или D-триггер {D - delay) имеет два входа: один для данньд data) и один для тактовых импульсов (CP - clock pulses). Для каждого тактово

пульса выход у принимает значение, которое имел вход D до него, т. е. выход от входа на один такт. Новое состояние никогда не зависит от старого.

Тактируемый триггер с одним входом Т, выход которого инвертируется кад такт, называется Т-триггером {T-toggle, переключатель состояния). Он применяе-rj в счетчиках и в схемах синхронизации как делитель частоты.

Функции всех трех вышеперечисленных элементов объединены в двухступен том (master-slave) JK-триггере, который имеет три входа - J (установки), К (сбро, и вход для тактовых импульсов. Это универсальный триггер, который в зависимост от входных сигналов работает как SR-, D- или Т-триггер и представляет собой ущ. нереальную двухпозиционную схему.

7.1.5. Реализация переключательных схем

Электронные логические элементы типа AND или OR можно непосредственв выполнить на диодах. Каскадное соединение нескольких диодных элементов создае некоторые проблемы, в том числе значительное ослабление сигнала на каждой стуш ни (диоды являются пассивными элементами), поэтому на практике такое решени не применяется. Типичный способ реализации логических цепей, позволяющий и бежать эту проблему, - применение транзисторной логики, поскольку выходно сигнал на каждой ступени усиливается до своего первоначального значения.

Сегодня логические элементы реализуются в основном на интегральных схемах (И( integrated circuit - 1С); другие названия - полупроводниковые кристаллы или микросхемы {chips). Существуют несколько типов интегральных схем, каждый из которых.ч; рактеризуется потребляемой мощностью и скоростью. В течение долгого времени испои зовались обычные схемы транзисторно-транзисторной логики (ТТЛ, transistor-transaH logic - TTL), но сейчас их вытесняют интегральные схемы других типов.

Элементы LS-TTL (маломощные ТТЛ-схемы с диодами Шотки, low-powerSchon TTL) включают в себя так называемые диоды Шотки, которые являются более быстр действующими по сравнению с обычными диодами и вдобавок потребляют меньш. мощность, чем ТТЛ-элементы более старых типов. Широко используются так*

iemen№ на оси

КМ ОН (комплиментарная структура металл-оксид-полупроводник, сотр metal-oxide semiconductor - CMOS) интегральные схемы, которые выполняют

ве полевых {field-effect transistors - FET), а не на биполярных транзисторов (?, transistors). Потребление мощности КМОП-схем на три порядка меньше, чем У ветствующих ТТЛ-элементов. Вдобавок КМОП-схемы менее чувствительны к эл ческим наводкам и изменениям питающего напряжения. С другой стороны, КМ схемы более чувствительны к статическому электричеству, а кроме того, Р°°ц;;

медленнее, чем соответствующие ТТЛ-схемы. Будущее, вероятно, за новым пок ем КМОП-схем - высокоскоростной КМОП-логикой {high-speed CMOS logic " j.

Сложные схемы могут быть выполнены в виде средних (СИС, Medium Integration - MSI) и больших (БИС, Large Scale Integration - LSI) интегра-", схем. Однако это экономически оправдано только при количестве компоненто

рядка нескольких тысяч. Альтернативой является использование так назЫВ* программируемых логических устройств {programmable logic device - PLD), °°рГ позволяют недорого производить универсальные И С. Большинство PLD частИ

еЖат к семейству LS-TTL. Они содержат большое количество элементов, свя-плавкими вставками {fuses). Используя специальное программируемое обо-ние, эти вставки можно избирательно выжечь, получив в результате ИС с тре-"(ЫМЧ логическими свойствами. 0 семействе PLD существует несколько типов ИС - программируемая логичес-jiaTpHua (ПЛМ, programmable array logic - PAL), логическая матрица, програм- уемая в процессе эксплуатации {field-programmable logic array - EPLA), програм-"oveMoe постоянное запоминающее устройство (ППЗУ, programmable read-only \einory - PROM). Схемы ПЛМ построены на программируемой матрице ;МО-элементов, соединенной с матрицей OR-элементов. FPLA-схемы имеют похо-кую структуру с той лишь разницей, что матрица OR-элементов также программи-9\ема. Существуют и специальные PAL- и FPLA-схемы с элементами NOR, XOR I, D-триггерами. Таким образом, систему последовательностного управления можно выполнить на основе одной или нескольких микросхем (рис. 7.14).

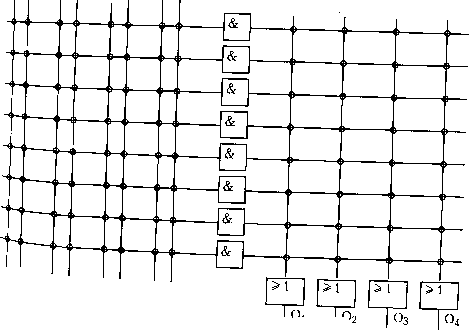матрица АЫВ

1 1

«с- 7.14. Функциональная структура схем PAL, FPLA и PROM функции программируемого логического устройства определяются пользователем. =зовая структура PLD состоит из матриц AND и OR, программирование которых вУЧествляется "выжиганием" связей между их элементами.

Схемах PAI m пм\мятгт.я AND поограммируема, а связи между элементами AND " OR aL. I о,плЛппТматрииа AND не меняется, а матрица OR про-См;Г Т"" JJ каждая комбинация входных бит (т. е. "адрес")

;мируема. В этом случае, напримеркажд значения из ад-

Ивиру„ д,, AND-элемент, а OR-матр матрицах AND и OR

, ""ои ячейки. FPLA допускает изменение