(6.36)

в результате алгоритм ПИ-регулятора принимает вид

Ud(kh) = К e(kh) + u0h)

где Ujikh) определяется из уравнения (6.35). В данном случае интегрирование апппп симировано разностями вперед вместо разностей назад. Такая замена необходим " скольку ujkh) должно быть известно до вычисления интегральной части. Этащощ фицированная и улучшенная процедура предотвращения интегрального насыщед [уравнения (6.35) и (6.36)] включена в алгоритм ПИД-регулятора в разделе 6.5 8

6.5.5. Плавный переход при изменении режима работы регулятора

При переключении с ручного на автоматический режим выход регулятора може измениться скачком, даже если ошибка управления равна нулю. Причина в том, интегральный член в алгоритме регулятора не всегда обязательно равен нулю. Реп. лятор является динамической системой, и интегральная часть представляет co6oi один из элементов внутреннего состояния, который должен быть известен при изменении режима управления. Скачок выходной величины регулятора можно предотвратить, а смена режима в этом случае называется плавным переходом {Ьитр1е& transfer). В этой связи рассмотрим две ситуации:

- переход с ручного на автоматический режим или наоборот;

- изменение параметров регулятора.

Плавный переход с ручного на автоматический режим для аналогового регулятора достигается за счет того, что процесс вручную приводится к состоянию, в котором измеренное значение выходной величины равно опорному. Процесс поддерживается в этом состоянии до тех пор, пока выходной сигнал регулятора равен нулю. В этом случае интегральная часть также равна нулю, и поскольку ошибка равна нулю, то достигается плавный переход. Та же процедура подходит и для цифровых регуляторов.

Другой метод состоит в медленном доведении опорного значения до необходимо!: конечной величины. Вначале опорное значение устанавливается равным текущем) измерению, а затем постепенно вручную доводится до желаемого. Если эта процед) ра выполняется достаточно медленно, интегральная часть сигнала регулятора оста ется настолько малой, что обеспечивается плавность перехода. Очевидным недостат ком этого способа является то, что он требует достаточно большого времени, котор" зависит от характера процесса. ,

ПИД-регулятор, основанный на алгоритме приращения [уравнение (-O) „ требует вышеописанной процедуры инициализации при изменении режима упр ления. Оператор устанавливает исполнительный механизм в положение, соот ствующее опорному значению, перед переключением с ручного режима на автом ческгн"!. В этом случае регулятор не вырабатывает никакого выходного сигнала исполнительного механизма до тех пор, пока не возникнет несоответствие м опорным значением и выходом процесса. Часто при использовании алгоритма ращения важно сохранить и абсолютную величину управляющего сигнала, пос ку оно может потребоваться позже для проверки.

Для цифровых ПИД-регуляторов существует еще одна возможность плав перехода. Алгоритм управления выполняется даже в режиме ручного управле Измеренное значение выходной величины у считывается регулятором, и вычисл ся ошибка управления, однако регулятор не вырабатывает выходной сигнал, влЯ

спизация ПИД-регулятора

процесс. В этом случае интегральная часть регулятора постоянно обновляет-рсли затем переключить регулятор в автоматический режим при условии, что ое значение равно текущему значению выходной величины процесса, смена °жима управления будет плавной.

" Основная идея всех процедур плавного перехода заключается в обновлении ин-егральной части регулятора до такого уровня, что управляющий сигнал остается не-[(зменным непосредственно перед и сразу после переключения режима.

Еше одна проблема возникает при изменении параметров ПИД-регулятора. Непосредственно перед этим выходной сигнал регулятора можно представить в следу-юшемвиде [ср. уравнение (6.20)]

U{t-) = + Up{t-) + Uj(t-) + Up){t-)

a сразу после изменения параметров

U{t+) = Uq + Up{t + ) + Uj(t+) + Uj)(t+)

Изменение одного или нескольких параметров повлияет на все части регулятора. Плавный переход от одного набора параметров к другому произойдет лишь в случае, если выход регулятора не изменится, т. е. u(t-) = u(t+), где t - момент изменения параметров. Значение интегральной или дифференциальной части должно быть откорректировано так, чтобы в момент переключения не произошло скачка выходного сигнала регулятора. Например, изменение интегральной части выражается следующим образом

Uj(t+) = Up(t-) + Uj{t-) + иф~) - Up(t+) - Upj{t+)

Плавный переход достигается, если разность u{t+) - u{t-) равна нулю.

6 5.6. Ограничение скорости изменения управляющего сигнала

ния° 1«ногих системах необходимо ограничивать амплитуду или скорость измене-управляющего сигнала. Для этого используются специальные схемы защиты, Дключаемые после канала ручного ввода опорного значения u{t) и передающие "видит™ ""Р"""™ сигнал Up{t), в результате процесс в действительности приме управляющий сигнал вместо введенного вручную. Такой способ обычно "ия си" регулировании электроприводов. Ограничение скорости изменена рис™ получить с помощью простой цепи обратной связи (рис. 6.14).

Сигнал "°аа"а также реакция на скачок опорного сигнала.

сравн Р""™ управления u{t), который должен выступать в качестве опорно-"Т>аничи" * допустимым управляющим сигналом Ui{t). Сначала их разность "Рчем стся пределами ме,.„ и ие. Затем полученное значение интегрируется, <ти из ""Р- аппроксимируется конечной суммой. Алгоритм ограничения ско-менения можно записать следующим образом

ие = ПС - uL;

if (ue < uemin) then uelim := uemin else if (ue < uemax) then uelim := ue

else uelim := uemax; uL = uL old-I-h*uelim;

(*функция ограничения*)

Глдва 6. С1р#Иуь управ п.

-1 к

время

Рис. 6.14. Цепь ограничения скорости изменения сигнала (в); типичная реакция на скачок опорного сигнала {б)

6.5.7. Вычислительные особенности алгоритма ПИД-регулятора

В реальности цифровая реализация ПИД-регулятора из-за последовательного >сарактера вычислений приводит к задержкам, которые отсутствуют при применении шалоговой технологии. Помимо этого, некоторые практические ограничения, такие как защита от насыщения и алгоритмы плавного перехода, требуют, чтобы выход регулятора и срабатывание исполнительного механизма происходили одновременно. Поэтому вычислительные задержки необходимо свести к минимуму. Например, некоторые элементы цифрового регулятора можно вычислить до момента выборки. Для регулятора с защитой от насыщения [уравнение (6.35)] интегральную часть можно записать следующим образом

(6.37)

uj[{k + \)h\ = Ujikh) + ci • e{kh) + C2 [u{kh) - ukh)]

Интегральную часть можно вычислить заранее с помощью разностей вперед, ференциальную часть [уравнение (6.29)] можно записать как

(6.38) , Диф-

ир,т=р • .( - т K-fii-)- [yikh) - у[(к - т

.Zk.(i-p).z/(M) + p-M(-i)/] + -f-(-P>-f

Ujjikh)-C-y(kh)+xl(k-l)h]

(6.35

x[{k - i)/z] = p • uiik - i)A]+ (1 - p) y[{k -m-

= -u[{k-\)h\+c-y{{k-\)h\ Состояние x можно обновить сразу после момента времени kh x(kh) = Р • u(kh) + сз • y{khy

= р • [-Сз y(kh) + x[(k - i)h]] + Сз - y(kh) = (6.41)

-x[(k~l)h] + cy{l-)-y(kh)

Таким образом, Up)[(k + 1)/г] удается вычислить из уравнения (6.39), как только получен результат измерения г/[( + 1)/г].

Учитывая вычислительные возможности современных компьютеров, может по казаться странным, что приходится затрачивать столько усилий на оптимизацик вычислений. Однако необходимо иметь в виду, что цифровой регулятор иногда должен выполнять несколько тысяч управляющих операций в секунду. В этих условиях н.\1еет значение, будут ли некоторые коэффициенты доступны сразу или их придется вычислять каждый раз заново. Кроме того, промышленные регуляторы, используемые в заводских условиях, не всегда изготавливаются на основе самых быстрых из имеющихся на рынке процессоров. Поэтому порядок и тип вычислений существенно в.таяют на скорость операций управления.

Промежуточные переменные Cj, С2 и С3 не имеют очевидной физической интерпретации. Вместо них оператор должен видеть значения основных параметров ПИД-регулятора К, Г,-, Ги Гу

Кроме уже сказанного, необходимо учитывать точность вычислений. В ПИД-ре-.адторе на основе алгоритма приращения вычисляются только малые величины, ност!™ которых достаточно короткого машинного слова. В то же время неточ-и округления в интегральной части могут вызвать проблемы, как упомянуто разделе 6.5.1. и . J

8.5.8.

"одЬгк"" пример программы ПИД-регулятора на языке Pascal. Вычисле-Pa.vie-rpQg "" Cj, С2 и С3 необходимо производить лишь в случае изменения па-•:ой регулятора К, Т, Ги 7)-. Алгоритм регулятора i

Алгоритм ПИД-регулятора

t выполняется в момент каж-

Ь1борки. Программа также содержит защиту от насыщения интегральный

эщей.

(* Предварительное вычисление коэффициентов * с1 .= K*h/Ti; с2 := h/Tt;

beta :=Td/(Td-b h*N); c3:= K*Td*(l -beta)/h; c4 := c3*(l - beta); ipart:= 0; x:= 0;

(* уравнение 6.38 *) (* уравнение 6.38 *) (* уравнение 6.28 *) (* уравнение 6.40 *) (* локальная константа *)

Глава 6. Структуры управлс

(* Алгоритм управления *) UC := AD input(chl);

у := AD input(ch2); е := UC - у; ppart := К*е; dpart := X - (сЗ*у);

ud := uO + ppart + ipart + dpart;

if (ud < uniin) then u := umin else if (ud < umax) then u := ud

else u ;= umax; DA output (chl, u);

(* ввод опорного значения, *)

(* аналоговый вход *)

(* ввод измерения, аналоговый вход»

(* вычисление ошибки управления *)

(* пропорциональная часть *)

(* дифференциальная часть, *)

(* уравнение (6.39) *)

(* выход регулятора до ограничения

(* сигнала *)

(* функция ограничения *)

(*вывод аналогового сигнала *) (*управления и, канал вывода #1*)

ipart := ipart + с1*е + c2*(u - ud); (* интегральная часть с *)

(* "антинасыщением", уравнение (6.35))

X ;= beta*x + с4*у; (*обновление состояния, *)

(*уравнение (6.41); с4 вычислено *) (*предварительно*)

Серийный ПИД-регулятор изображен на рис. 6.15. На передней панели регулятора отображаются опорные и текущие значения выходных величин процесса. Переключение с ручного режима на автоматический осуществляется кнопками. Прочие клавиши используются для изменения опорных значений и настройки других параметров регулятора.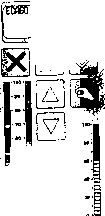

Р„с. 6.15. Сер,йиь™ ПИД-регулятор (с разрешения компании Alfa L.v.l Auto«»

Швеция)

саяизация ПИД-регулятора

5 9 Применение проблемно-ориентированного блочного языка

алгоритмов регулятора можно использовать любой последовательный язык про-гоования. Однако на практике обычно используются проблемно-ориентирован-языкл высокого уровня, так называемые блочные языки (block languages). Как и для " аммяруемых логических контроллеров (раздел 7.3), функции управления принято "Р но изображать в виде блоков, на которых помечены лишь входные и выходные сиг-° а сам алгоритм не отображается. Естественно, что параметры управления могут

зменяться управляющим компьютером. На рис. 6.16 показано типичное описание рд.регулятора на блочном языке. Разработчик с помощью специальных программных

педств должен лишь пометить входы и выходы каждого блока регулятора соответствующими именами переменных и затем соединить блоки между собой и с другами элементами схемы. Все это выполняется непосредственно на экране компьютера.

R.21

R.22 -J

R.23

R.24

R.25

ON AUTO UEXT REF

FB HI

LO К Ti Td

0.2 2.0 0.3

R.29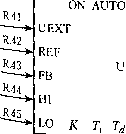

0.1 3.0 0.4

R.59

max min CH

1.0 0.0 4

output

R.49

6.16. Функциональная блок-схема из двух ПИД-регуляторов, подключенных ""«одному аналоговому устройству через селектор

Рисунке представлены два ПИД-регулятора, присоединенных к переключате-„ Ь1ход одного из двух регуляторов выбирается с помощью двоичного сигнала, йы?*ого на переключатель; затем выбранноезначение поступает на аналоговый ц °«ой блок. Вход AUTO представляет соЬои двоичную переменную для пере-ения с ручного на автоматический режим управления. Опорное .значение пода-