Значение x[(k-iЩ к моменту времени kh уже вычислено, так что задержки

занные с компьютерной обработкой, минимальны. Как только вычислен сигнал равления u(kh), можно получить новое значением, которое будет использованоДJ, вычисления сигнала управления на следующем щаге выборки (рис. 6.26).

измерительной информации обновление

измерительной информации обновление y{kh) x{kh)

ввод

измерительной информации обновление

уфт х[(к+щ

вычисление u[(k-\)h\

вычисление u{kh)

вычисление u[(k+i)h]

время

(k-i)h kh (k+l)h

Рис. 6.26. Последовательность вычислений для обобщенного регулятора

6.9.5. Алгоритм обобщенного регулятора

Приведенный алгоритм базируется на уравнении (6.60) и включает код для прс дотвращения интегрального насыщения. Параметры регулятора уже преобразован!/ из стандартной формы во внутреннее представление. В этой программе на язык-. Pascal учтены требования работы в режиме реального времени - защита ресурсов, синхронизация задач.

program general controller const n = 5;

ш = 5;

(* пример обобщенного регулятора *) (* степень управляющего полинома *) (* степень упреждающего полинома *) (* по возмущению; т>п*)

var vectprotect; semaphore;

next time, delta time: time (real);

i, j; integer;

out signal, x: real;

u, uc, y, w: array[0..n] of real;

R, S, T, V: array[0..n] of real;

begin

x := 0;

vect protect ;= 1;

(* инициализация векторов состояния *) for i = о to n do begin

u[i]:=0; uc[i] := 0; y[ij := 0; w[i]:=0; end

while true do begin

(* ввод текущих значений *) wait until(next time); uc[0] := ADJnput (ch#l); y[0] := ADJnput (ch#2); w[0] ;= ADJnput (ch#3);

(* основной бесконечный цикл *)

(* ввод опорного значении-*) (* ввод измерений *) (* ввод возмущения *)

(* вычисление управляющего сигнала *)

wait(vect protect);

(* защита доступа

(* к управляющему полиному *) S[0] * у[0] - V0 * w[0] + х;

(* снятие защиты *)

(* управляющего полинома *) DA output (out signal, ch#10);(* вывод сигналов управления *)

out signal := Т[0] * ис[0] signaI(vect protect);

(* обновление векторов состояния *) и[0] : out signal; for i = п downto 1 do begin

j := i - 1; u[i] := u[j]; uc[i] :=uc[j];

y[i]:=yD];

end;

for i = m downto 1 do w[i] := w[i - 1]; (* расчет значения x *) x:=0;

for i = 1 to n do begin

x:=x-R[i] *u[i]; x:=x + T[i]*uc[i]; x:=x-S[i]*y[i]; end;

for i = 1 to m do X := X - V[i] * w[i]; next Jime := next time + delta time; end; (* основной цикл *)

end; (* обобщенный регулятор *)

роГГазГ 10 ЛГ1 "Р" °бщим

Чами • - Как правило, к этим переменным имеет доступ только под-

ЩпТ РУ™Р серьезных задержек обработки возникать не должно

-другая программа получает доступ к коэффициентам регулятора, например для

Главаб. Структуры упра

их обновления, тогда процедура регулятора должна ждать во избежание конЛ В многозадачном режиме программа регулятора имеет более высокий приор" чем программа, изменяющая коэффициенты. Переменная nextjime используй для того, чтобы избежать ошибок синхронизации (раздел 10.6.5).

Как уже неоднократно отмечалось, коэффициенты полиномов обобщенного ре лятора не имеют прямой связи с физическими свойствами контура управлен Только в самых простых регуляторах соотношения между коэффициентами и фи-ческими свойствами контура управления имеют очевидный смысл.

В П-регуляторе все коэффициенты, кроме Sq и q, равны нулю. Количество коз фициентов 5j и отличных от нуля, задает порядок дискретного управнен! ПИД-регулятор имеет второй порядок, поэтому первые три коэффициента в полит мах R, S яТ ненулевые, а все остальные равны нулю [уравнение (6.52)]. В конт\ упреждающего управления по возмущениям процесса некоторые из коэффициент полинома К ненулевые, и то же самое справедливо в отношении контура упреждак щего управления по опорному значению и полинома Т.

В случае регулятора Смита для компенсации задержек в техническом процесс коэффициенты полинома R отличны от нуля, так что предыдущие управляющие сигналы сохраняются в течение такого количества интервалов выборки, которое сот ветствует времени задержки Tgiy плюс порядок системы п - если Tgiy равно 4 интервалам выборки, а порядок системы равен 2, то старые значения хранятся в теченш 6 интервалов.

Если изменяется интервал выборки, то необходимо изменить и размерность по.и: номов R,S,Tm у для того, чтобы дискретные значения переменных с течением времс ни сдвигались назад и были доступны для вычисления нового управляющего сигнс ла.

Ниже приведена программа ввода новых параметров ПИД-регулятора, их прес-разования в коэффициенты полиномов R,SviTm оперативного обновления этих к эффициентов, т. е. без прерывания работы регулятора.

procedure parameter input

(* оперативный ввод параметров ПИД-регулятора *)

(* и их преобразование в коэффициенты полиномов R, S и Т *) const п = 5; (* степень управляющего полинома *)

var К, Ti, Td, N, sample h: real;

C alfa, C beta, C gamma; real;

R, S, T: array [0..n] of real;

begin

while true do (* бесконечный цикл *) begin

writeln ("Введите следующие параметры");

input "Коэффициент усиления К ?", К;

input "Постоянная времени интегрирования Ti ?", Ti;

input "Постоянная времени дифференцирования Td ?", Td;

input "Нормирующий коэффициент N ?", N; (* уравнение (6.15)

input "Интервал выборки h", sample h;

пбратная связь по переменным состояния

(* вычисление новых коэффициентов *) C alfa := sample h / Ti; C beta := Td / (Td + sample h * N); C gamma := Td * (1 - C beta)/sample h;

(* уравнение (6.23) *) (* уравнение (6.28) *) (* уравнение (6.53) *)

(* вычисление новых коэффициентов полиномов*)

wait(vect protect); (* защита доступа *)

(* к управляющему полиному *)

R[0] := 0;

R[l] :=-1 - C beta;

R[2] ;= C beta;

T[0]-.= K*(1 + C alfa);

T[l] := -К * (1 + C beta + C alfa * C beta);

T[2] := К * C beta;

S[0]:=T[0]+K*C gamma;

S[l] := T[l] - 2 * К * C gamma;

S[2] := T[2] + К * C gamma;

signal(vect protect); (* снятие защиты *)

(* управляющего полинома *)

end; (* бесконечного цикла *) end; (* parameter input *)

Процедура parameterj-nput является универсальной, поскольку с ее помощью можно вводить не только коэффициенты полиномов R, S, Ти V, но и прочие параметры, используя для этого как стандартный ввод (клавиатуру), так и другие интерфейсы. То есть свойства системы управления можно изменять, не переписывая програм-У заново. Приведенную программу можно также использовать как часть адаптивного регулятора. В этом случае другая процедура должна постоянно вычислять новые параметры для полиномов R, S чТпа основании последовательностей "W) и г/(:/г) и соответственно корректировать их.

610. Обратная связь по переменным состояния

До сих пор в этой главе динамические системы описывались своими непре- ВДыми передаточными функциями или дискретными передаточными оператора-.\1н ° "Означает, что выявлялись только соотношения между входными и выходны-Bhv "иыми, а регуляторы описывались только в виде отношения вход/выход.

Ренние связи процесса были скрыты и в явном виде не формулировались, тоян """ случаях, однако, более удобно описывать процесс в пространстве со-\Щ н " внутреннее описание приводит к другой управляющей структуре, кото-

азывается обратной связью по переменным состояния {state feedback). iipg "иое дискретное описание системы в пространстве состояний было дано •• 3.4.1 [уравнение (3.9)]; с его помощью можно описать систему с нескольки-Чи выходами. Параметры системы обычно имеют физическую интерпре-\,(. поскольку уравнения выводятся на основании уравнений баланса сил, мо-Массы или энергии.

Глава6. Структурыупрд

Модель в пространстве состояний представляет основу для проектировд ратной связи по переменным состояния системы с произвольным количество) ных и выходных переменных

и(0 = М • u(t) - L • х(0 где М и L - матрицы, а - опорное значение сигнала (рис. 6.27).

(6.61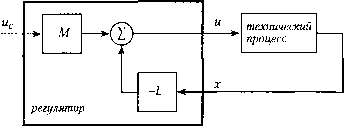

Рис. 6.27. Структура регулятора с обратной связью по переменным состояния В случае одной выходной переменной закон управления приобретает следующий bi u(t) = т u{t) -11 xi(t) - I2 X2(t) - ... - /„ • x„(t)

где 772, /j,- постоянные. В принципе, обратная связь по переменным состояш есть сумма выходных сигналов пропорциональных регуляторов - по одному сигк лу на каждую переменную состояния.

Если переменная состояния неизвестна или ее нельзя непосредственно измерит то для нее применяется процедура либо косвенного вычисления, либо оценки (ра дел 3.5.2), результат которой включается в уравнение регулятора.

Считая, что все переменные состояния измеряемы и известны, замкнутая chctcn с обратной связью по переменным состояния описывается следующим ypaBHCHHCN

x[(k + 1)/г] = Ф • x(kh) + Г • [М • u(kh) - L • х(М)] =

= (Ф - Г • L) • x(kh) + Г • М • u{kh)

[Мй1

(6.6

Матрицы Ф и Г зависят от вида процесса и не могут изменяться, а матрицы

можно настраивать. Выход регулятора остается постоянным между моментами борки и рассчитывается с помощью матричных операций над данными измерь известными в момент у/г. -гП-Г

Динамика замкнутой системы [уравнение (6.62)] описывается матрицей Ф Собственные числа этой матрицы определяют динамические свойства систем ратной связью. Если система является управляемой, эти собственные числа f- произвольно изменить, настраивая параметры регулятора с помощью атр" ,, Точно так же, как и для регулятора, описанного отношением вход/выход, Д ческие свойства замкнутой системы можно произвольно изменить, при услов! управляющие сигналы не ограничены. Однако и в этом случае имеются опреД ные практические ограничения. ,

Собстеенные числа (полюса) управляемой технической системы можно йзм на основе обратной связи по переменным состояния точно так же, как и у регУ-",,

оП"- соответствующую структуру регулятора.

6.11

заключение

обратная связь имеет фундаментальное значение в любых системах управления, ессами. Основные выводы, касающиеся обратной связи, одинаковы и для анало-и для дискретных систем. Аналоговый и дискретный линейные регуляторы "меют одинаковую структуру, но разные значения параметров. С точки зрения про-

* даптрования разные типы линейных регуляторов легко получаются как частные ;учаи алгоритма обобщенного регулятора.

Есть два способа проектирования цифровых регуляторов. . Сначала разрабатывается аналоговый рег}лятор, а затем строится его дискретная модель.

• Вначале разрабатывается дискретная модель технического процесса, а затем на базе этой модели создается дискретный регулятор.

В этой главе применялся в основном первый способ. Недостаток такого подхода йключается в том, что требуемый интервал выборки получается меньше, чем при непосредственном проектировании дискретного регулятора.

Важнейшей концепцией является упреждающее управление. Эта структура по--могает расширить и улучшить свойства регулятора. Например, в высокоточных сервоприводах применение этого подхода позволяет более строго придерживаться опорного значения. В управлении процессами очень важно обеспечить как можно оолее раннюю компенсацию измеряемых возмущений и изменений нагрузки. В принципе, передаточная функция от опорного значения к выходной величине должна иметь значительный коэффициент усиления во всем диапазоне рабочих частот,

•передаточная функция от возмущения к выходной величине - минимальное уси-

ение.

ПИД-регулятор - это наиболее распространенная структура управления в про-ленных системах. Причина его популярности в том, что большинство процессов аппроксимировать динамической моделью невысокого порядка. ПИД-регу-в" Щп!,!"™ собой систему второго порядка, дает практичное и недоро-

•иров""™ °"*вая большую гибкость при работе в замкнутых системах регу-Реи.Г" Р™ вариант ПИД-регулятора обладает дополнительными - J ствами. Например, в дискретный регулятор значительно проще включают-

"1

""Я- Kd " плавного перехода и предотвращения режима интегрального насыще-мо*и" °f° он обеспечивает необходимое качество фильтрации при регулиро-

fPan

производной. При необходимости цифровой регулятор

но к величину управляющего сигнала, так и скорость его изменения. Воз-

CTBv """ соединение ПИД-регуляторов, если несколько переменных взамо-уют между собой сложным образом.

-регулятор не подходит для системы с более сложными динамичес-•8ств Наиболее очевидные проблемы возникают в системах с зонами не-

ительности и запаздываниями, с ярко выраженной колебательной динамикой ,)ад"Р*етрами, меняющимися во времени. Обобщенный дискретный регулятор Ляет не только справляться со всеми этими проблемами, но и отвечает еще бо-

позволяет легко

описанного

отношением вход/выход. Разница заключается в том, что внутри