управляющий компьютер

проверка входных сигналов

цифровая фильтрация

прикладная обработка

проверка

выходных

сигналов

АЦ-преобразованиеЛ

мультиплексирование

аналоговая фильтрация

входные данные

выходные данные

согласование сигналов

датчики

физический/ технический процесс

Рис. 5.1. Схема ввода/вывода в системе "процесс-управляющий компьютер"

5.1.2. Мультиплексоры

Во многих случаях различные элементы системы должны совместно исп ватГнекоторые ограниченные ресурсы, например входной порт компьютер длинный сигнальный кабель, по которому передается информация от нескол датчиков Мультиплексирование (multiplexing) позволяет компьютеру в любоК датчиков, i ly :„„оп к-якого латчика необходимо считать. Иначе гоВ"!-

мент времени выбирать, сигнал какого датчг

мул1типлисор (multiplexer) можно рассматривать как переключатель (коммутат

кзщий компьютер в каждый момент времени только с одним датчиком соединя j .j.jjjjgj(;j.ipoBaHHe применяется не только в области измерений, но и (ри и в другом смысле, важную роль в технике связи (раздел 9.4.2). играет- X

задающий таймер

аналоговые входы

сигналы синхронизации

АЦ-преобразователь со схемой выборки и хранения

выходные щфровые данные

Рис. 5.2. Мультиплексирование и АЦ-преобразование измерительной информации

Мультиплексор может быть либо электромеханическим, либо электронным. Если считать, что все входы мультиплексора пронумерованы, то переключение обычно происходит последовательно в соответствии с порядковым номером; однако применяются и другие алгоритмы. Электромеханический мультиплексор с язычковым реле - надежная, хотя до некоторой степени медленная, система; он может выполнять до сотни коммутаций в секунду. Эксплуатационный период мультиплексоров этого типа ограничен естественным износом подвижных частей, хотя, с другой стороны, такие системы имеют хорошие изолирующие качества и низкую стоимость. Другой немаловажный фактор - очень малое падение напряжения на контактах. Для сравнения: электронный полупроводниковый мультиплексор намного быстрее (коммутация занимает не более чем несколько микросекунд). В сочетании с развязывающим усилителем (раздел 4.5.1) этот тип мультиплексоров имеет очень хорошие эксплуатационные характеристики, но он существенно дороже релейного мультиплексора.

Токовые утечки и скачки напряжения на входах мультиплексора могут представлять собой серьезную проблему. Развязывающий усилитель между датчиком и компьютером работает с дифференциальным входом, но потенциал сигнала может плавать" относительно "земли". В этом случае проводники, подходящие к мультиплексору или АЦП, должны быть гальванически изолированы, например с помо-

ю переключаемого проходного конденсатора (пример 4.9, раздел 4.5.3).

1.3. Дискретизация сигналов

оговы было показано, что компьютер не может непрерывно считывать ана-пьют тналы, а выбирает их только в некоторые моменты времени. Поэтому ком-Рети °"Р"нмает сигнал в виде последовательности дискретных значений. Дис-читы (.sampling) - выборка, оцифровка, квантование - представляет собой ется в сигнала только в определенные моменты времени; этот процесс реализу-"ание дТтере специальной схемой. Дискретизация включает мультиплексиро-с i,Qj "Преобразование. Эти операции должны быть строго синхронизированы

0Щью задающего таймера (рис. 5.2). "Роб "° " дискретизация происходит очень быстро. Однако во время АЦ-Мог,!, 5*ния должно быть каких-либо изменений во входном сигнале, которые Хра повлиять на цифровой выход. Это обеспечивается операцией выборки и (sample-and-hold) в каждом цикле дискретизации - значение аналогового

рое обычно существенно дороже мультиплексора для всех входных сигналов. Пр, разование аналогового сигнала в цифровой происходит в аналого-цифровом пр разователе (АЦП). Схема выборки и хранения запоминает мгновенные значки входного сигнала в заранее установленные моменты времени и удерживает его стоянным на выходе в течение интерва.та дискретизации. Перед дальнейшей ogp боткой в компьютере значение сигнала измерительной информации необходимо полнительно проверить, чтобы удостовериться в том, что оно приемлемо и имее, смысл в контексте физического процесса.

сигнала считывается в начале каждого интервала и остается постоянным в тр всего времени АЦ-преобразования. Эта операция называется задержкой нут,** порядка (рис. 5.3). Такой подход был использован при численном моделиро нелинейных систем (раздел 3.3.7) и при дискретизации по времени HenpepbiBHbD,"" намических систем (раздел 3.4).

выходной (квантованный)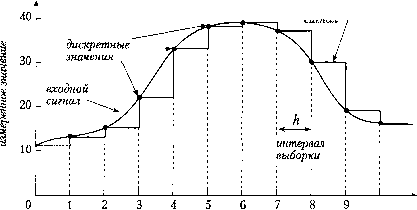

10 время

Рис. 5.3. Дискретизация аналогового сигнала с задержкой нулевого порядка

Схема выборки и хранения {sample-and-hold circuit) показана на рис. 5.4. Ее рабоп управляется ключом. В моменты выборки {S - sample) ключ замыкается и конденсатор С заряжается до текущего значения напряжения входного сигнала. Во вре» удержания (Я - hold) ключ открыт и на выходе операционного усилителя сигна. в идеальном случае остается постоянным и равен последнему выходному значеня в момент, когда ключ был еще замкнут.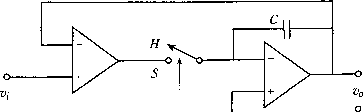

управление режимом работы

Рис. 5.4. Схема выборки и хранения с единичным усилением К-

В режиме выборки (5 - sample) амплитуда выходного сигнала равна мгновенному нию входного сигнала o„ = В режиме удержания {Н - hold) выходной сигнал "ОС , и равен последнему выходному значению, когда цепь функционировала в режиме вь

Дискретный сигнал отстает примерно на половину интервала дискретиза, относительно непрерывного сигнала. Если процедура дискретизации является тью большой системы управления, эта задержка может вызвать фазовое отставай привести к сокращению диапазона устойчивости цифрового регулятора по сра нию с соответствующим аналоговым устройством (раздел 6.5.2).

дискр?!

4 опреД®" интервала дискретизации

.,к-нп ппавильно определить интервал дискретизации аналогового сиг-Очень важпи f

общем случае это представляет собой нетривиальную задачу. Интервал пии h должен быть достаточно коротким, чтобы выходной сигнал " ле.мой точностью описывал изменения аналогового входа. Теоретически ""та дискретизации должна более чем в два раза превышать частоту наивыс-"составляющей преобразуемого сигнала (частотные компоненты определяют-"" помощью Фурье-анализа исходного сигнала). Если интервал дискретизации ишком велик, т. е. частота выборки слишком мала, то компьютер получит не-" цукз картину исходного сигнала. В то же время слишком малый интервал, е высокая частота выборки, приводит к тому, что управляющий компьютер выполняет неоправданно много вычислений. Кроме того, чем больше быстродействие - тем дороже устройство.

Поскольку после выборки об исходном сигнале ничего не известно до следующей выборки, период дискретизации должен быть настолько коротким, чтобы исходный сигнал не успел значительно измениться. Другими словами, частота выборки должна быть достаточной для последующего восстановления аналогового сигнала из дискретного. Нижний предел частоты, очевидно, связан с динамикой процесса, т. е. насколько быстро измерительный сигнал, а следовательно, и первоначальная физическая величина изменяются во времени. Ключевой задачей дискретизации является сбор достаточной информации для последующей обработки сигнала, например для генерации необходимых выходных сигналов в системе управления с обратной связью.

Выбор интервала дискретизации проиллюстрирован ниже на примерах. Для простоты обсуждение ограничено синусоидальными сигналами. Однако поскольку каждый сигнал можно разложить на совокупность гармоник, например с помощью пре-0 разования Фурье, то дальнейшее изложение справедливо для любых аналоговых сигналов.

Примерз.1 а

Дискретизация синусоидального сигнала

Рассмотрим аналоговый синусоидальный сигнал с частотой /. Этот сигнал кретизируется с частотой Д.. Если выборка делается шесть раз за период дного сигнала, то гладкая кривая, проведенная через эти точки, близка (рис™ наблюдаемая частота не отличается от исходной частоты / кривая делать выборки только три раза за период, то результирующая Мая ч " "енее надежное представление исходного сигнала, хотя наблюдае-

частота/ все еще равна частоте/, орок" Дпьш сигнал дискретизируется только 5/4 раз за период (т. е. 5 вы-(рис5 периода), то соответствующая гладкая кривая также синусоидальна Част наблюдаемая частотаравна 4, т. е. намного меньше истинной

Кп с;-.У-- Наблюдаемая ложная частота есть разность между частотой выбор- "7/4 и

истинной частотой /. Эта ложная, или кажущаяся, частота называет-

;очастотой {alias frequency).

еремя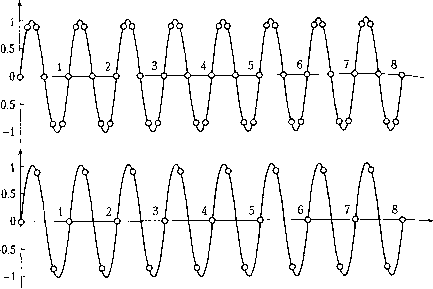

время

Рис. 5.5. Если синусоидальный сигнал дискретизируется шесть или три раза за период, наблюдаемая частота равна истинной

исходный сигнал

восстановленный сигнал (задержка первого порядка) \

наблюдаемый сигнал (аппроксимация выборки)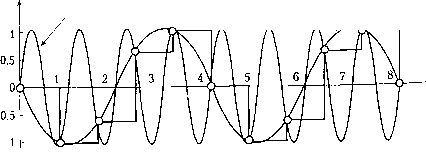

время

Рис. 5.6. Если синусоидальный сигнал дискретизируется пять раз за четыре периода то наблюдаемая (аппроксимирующая) синусоида будет иметь намного более низку» частоту, чем исходная

Отметим следующий эффект; если частота выборки слишком мала по отноше" к частотным составляющим исходного сигнала, то в восстановленном сигнале появл ся ложная частота (псевдочастота), как показано в примере 5.1 а. Наблюдаемая част /„ (псевдочастота) есть разность между частотой выборки/, и истинной частотой/

Частота восстановленного сигнала (наблюдаемая частота) будет той же са что и исходная, до тех пор пока частота выборки достаточно высока, т. е./<. > 2/

< 2/ наблюдаемая частота уменьшается линейно и достигает нуля при / = при одной выборке за период. Если выборка происходит один раз за период (или

очевидно, что исходный сигнал выбирается всегда в одной и той же периодо")™рддР5ческого сигнала будет получено одно и то же значение; другими фазе и Д-1Я даемая частота становится нулевой. Зависимость между наблюдае-словами, цденной) и истинной частотами имеет пилообразный вид (рис. 5.7). sfOH (восста

/о/Л 0.5

/дг [частота Найквиста]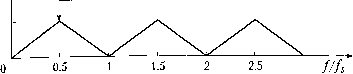

Рис. 5.7. Наблюдаемая частота fg как функция истинной частоты/синусоидального сигнала при частоте выборки/,.. Наблюдаемая частота равна истинной частоте, только если /,<0.5,те.Л>2/

Оказывается, что при частоте выборки /, меньшей удвоенной частоты исходного сигнала/, последний нельзя восстановить на основании дискретных значений. Граничная частота называется частотой Найквиста (Nyquist frequency)

(5-1)

Если аналоговый сигнал содержит любые частоты, превышающие /дг/2, то эти высокочастотные компоненты появляются в последовательности данных выборки как гармоники более низкой (псевдо) частоты. Во избежание появления псевдочастот необходимо, чтобы частота выборки по крайней мере вдвое превышала самый высокочастотный компонент сигнала. В этом суть теоремы дискретизации (sampling theorem).

На практике частота выборки должна быть больше частоты Найквиста. Теорема основана на предположении, что исходный сигнал периодический и дискретизируется неофаниченное время. Поскольку очевидно, что в реальных системах это не так, то для сбора информации, достаточной для адекватного описания сигнала и его пос-чедующего восстановления, частота выборки должна быть выше. Более того, в случае непериодического сигнала нет теоремы, ограничивающей нижний предел частоты выборки. Несколько практических правил для частоты выборки в замкнутых " управления рассматриваются в разделе 6.5.2. оычно аналоговый сигнал содержит высокочастотный шум. Поэтому частота вы-Щей " определяться по самой высокочастотной составляющей, присутствую-зоп сВДном сигнале. Все частоты, превышающие половину частоты Найквиста, ка*"" Ь1ть удалены из сигнала до дискретизации, в противном случае они появятся щиещ астоты в выходном сигнале. Этот принцип иногда толкуют так; интересую-щ частоты должны быть ниже, чем половина частоты Найквиста. Очевидно, что Чоя частоты, превышающие половину частоты Найквиста, приводят

сли псевдочастот, независимо от того, представляют они интерес или нет. Щ ""окочастотный шум налагается на низкочастотный сигнал, то выборка с часто-Нал нной только по низкочастотному сигналу, даст искаженные значения из-°Нен°*" посторонних компонентов на полезный сигнал. Высокочастотные ком-Чрот можно подавить либо удалить аналоговым фильтром низких частот

во-псевдочастотным фильтром), как это описано в разделах 5.3.1 и 5.3,2.

•и частотой Котельникова. - Примеч. ред.