в верхней части рисунка изображен технический процесс, а в нижней - т, ра его оценки по всем переменным состояния {full-order estimator), т. е. компьа"* модель на основе уравнений (3.17). Другими словами, оценка есть не что и компьютерная модель технического процесса, которая регулярно корректно основе текущих измерений. Для проверки сходимости используется величин" рая называется погрешностю оценки {estimation error)

x{kh) = x{kh) - x{kh)

Вычитая уравнение (3.17) из уравнения (3.9) и подставляя уравнение (3 Ю) условии, что матрица D нулевая, имеем

x[{k + i)h] = Ф x{kh) - К • [y{kh) - С • x{kh)] =

= Ф x{kh) -КС x{kh) = (Ф - К • С) Si{kh)

(3.18,

Если К можно выбрать так, что x{kh) сходится достаточно быстро к нулю, то оценка является удовлетворительной. Это означает, что x{kh) будет сходиться к х{Щш-зависимо от начальных условий. Более того, К можно подобрать таким образом,™ погрешность будет сходиться быстрее, чем исходная аппроксимация, определяема; матрицей Ф.

Возможность выбрать К таким образом, чтобы оценка была приемлемой, зависш от наблюдаемости системы, которая определяется только матрицами Ф и С. Инач! говоря, наблюдаемость характеризует возможность получить информацию o6oBcei состояниях системы х на основе выходных сигналов у. Наблюдаемость также гарантирует, что можно найти подходящую матрицу К такую, что x{kh) сходится к нулю сколь угодно быстро. Ненаблюдаемость означает, что некоторые состояния или части системы физически отсоединены от выхода процесса и поэтому не отражены виз-мерениях. Система, описываемая передаточной функцией, наблюдаема, если числитель и знаменатель не имеют общих множителей.

Пример 3.18

Оценка угловой скорости в механической системе

Рассмотрим двигатель, соединенный с тяжелой нагрузкой упругим валом-В бумагоделательной машине или на прокатном стане упругость вала может быть причиной колебаний нагрузки (рис. 3.18).

т 1.

Рис. 3.18. Электрический привод, состоящий из двигателя и нагрузки, соедиие упругим валом

ннЫХ

Поскольку основной целью является управление угловой скоростью грузки, эту скорость нужно измерять. Скорость также можно оценить, еС измерить угловое положение нагрузки. Динамика нагрузки описывается зако

-" Упругий вал действует как пружина с силой реакции, пропорци-

ном Ньютона. R ежду углами поворота валов двигателя и нагрузки. До-

ональной P""jp(,.i.b скоростей вращения (о валов двигателя и нагрузки вы-

полнительно Р ддения, пропорциональный скорости. При моменте

зывает енте инерции закон Ньютона для нагрузки имеет вид

двигателя У,„

, d

динамику системы можно описать уравнениями состояния

dc dt

со

dx2 ~dt

x--r-x2 + - -T„, Jl

y{t) = Xy

Производные аппроксимируются конечными разностями с шагом h x[{k+\)h]Xy{kh) + h-x2{kh)

kh he Л

x2[{k + 1)/г] - x2{kh) - - • x{kh) - - • x2{kh) + - TJkh) Jl Jl Jl

где = 0,1,2,... Оценка имеет вид

xi[{k + i)h] -xy{kh) + h x2{kh) + [x{kh) - xy{kh)]

Tm(kh) +

, , kh he h

iKk + \)h] = x2{kh) - - xy{kh) - - x2{kh) + -

Jl Jl Jl

+ K2-[x,{kh)-x,{kh)]

Цель оценки - вычислить x2{kh) на основе измерений у = x{kh). Началь->ie условия реальной системы неизвестны, и поэтому для оценки их можно II ть нулевыми. В примере, показанном на рис. 3.19, угловая скорость меха-Угл Системы изменяется неизвестным образом. В момент времени t= 5 тви орость меняется скачком из-за мгновенного увеличения момента корост рисунке видно, как значение х2 стремится к x2{kh). Реальная ны о 2{kh) неизвестна и принимается равной 5. Даже если icj и К2 рав-pg.j,°p"* стремится к реальной величине, поскольку модель оценки кор-ствите значения и К2 положительны, оценка может сходиться к дей-холп значению быстрее. Чем больше значения и К,, тем быстрее

ji тся оценка.

onejjj У оценка достигла действительного значения (т. е. погрешность ОДиой ну-лю), то они и дальше остаются идентичными, даже если Ункци}о°~ изменяется; в известном смысле оценка "знает" входную

Глава 3. Описание vmmmpoBai

скорость 6 5 4 3 2 1 О -1 -2 -3 -4

Рис. 3.19. Оценка скорости на основе точного измерения угла поворота различных значений вектора оценки К. Реальная скорость показана сплошной линией, а оценки - пунктиром. Значения вектора оценки: 1 - iC, = О if = о 2 - = 3, = 3; 3 - = 3, ii:2 = 15. Оценки 2 и 3 сходятся быстро - они совпадают с реальной скоростью примерно через 2 секунды. Следует отметить что оценки 2 и 3 первоначально имеют разные знаки

В реальной системе скорость можно получить просто дифференцированием угла поворота вала. Однако на практике это довольно сложная операция, поскольку сигнал обычно зашумлен и производная от такого сигнала дает мало информации.

неопределенно:

Если модель физической системы неточна, то динамика погрешности не подчиш ется уравнению (3.18). Однако часто К можно выбрать таким образом, что систем: остается устойчивой, а погрешность оценки приемлемо мала, даже несмотря на не большие неточности в модели процесса или искажения при измерениях. Этому посвящен следующий раздел.

3.6. Системы с неопределенностью

Математическая модель редко точно отражает реальность - всякое описание строится на основе некоторых допущений. Во многих случаях модель не учитывав все тонкости реального процесса, а некоторыми состояниями просто пренебрега"" Существуют системы, которые трудно описать количественно в виде математиче ких выражений. В таких случаях можно использовать семантическое описан в частности для систем, в контур управления которых включен человек-опера К этому классу относится большинство биологических систем, которые либо сл ком сложны, либо недостаточно изучены. Поэтому при проектировании систем У равления всегда необходимо задаваться вопросом о том, какая модель явля наиболее адекватной с позиций неучтенных факторов - неопределенно {uncertainties).

Моделирование возмущений и случайных ошибок в датчиках основываете теории стохастических процессов. Стохастический процесс {stochasticprocess) последовательность случайных величин. В принципе это означает, что в момен

ьорки к значению--зрояности. Аналогично, шум в изм с известным Jу добавку к сигналу датчика. Проблемы

каждой переменной процесса добавляется случайная величина

измерениях можно точности изме-

Оценка состояния при стохастических возмущениях

" разделе предполагалось, что используемая при оценке измери-

В "PJ (т. е. вектор измерений у) не содержит ошибок. На практике не

тельная ""Ljx датчиков. Шумы и возмущения в датчике можно рассматри-сушествует и случайную переменную е в уравнении состояния. Возму-вать на все датчики технического процесса, можно компактно записать Sc"вГкторе, который добавляется в уравнение (3.10)

y{kh) - С x{kh) + e{kh) (3.19)

Каждый компонент вектора шума e{kh) моделируется как последовательность стохастических, т. е. случайных, значений. Если эти компоненты независимы друг от друга, тогда амплитуды компонентов шума в момент времени kh не зависят от их значений в предшествующие моменты времени. Обычно, можно считать, что эти амплитуды нормально распределены, и тогда среднее значение и стандартное отклонение полностью характеризуют возмущения.

При наличии шума в измерениях процедура оценки, описанная в разделе 3.5.2, должна выполняться с особой тщательностью. Для вычисления погрешности вместо уравнения (3.10) используется уравнение (3.19). Выражение для оценки принимает вид

х[( + l)h] = Ф • x{kh) + Г • VL{kh) + к • [y{kh) - с x{kh)] =

= Ф • x{kh) + Г • xx{kh) + К • [С • x{kh) + e{kh) - С x{kh)]

(3.20)

В этом случае необходим компромисс при выборе К. Большие значения компонентов вектора К ускоряют сходимость, но при этом усиливается влияние слагаемо- шума е, что увеличивает погрешность оценки. Поэтому значения компонентов ™Р должны быть, с одной стороны, достаточно велики, чтобы x{kh) сходилось t(kh\ °ожно быстрее, а с другой - достаточно малы, чтобы слагаемое шумг ) не очень существенно влияло на результат.

Ченка при зашумленных измерениях

чтоа " механическую систему из примера 3.18. Предположим, результаты измерения угла поворота вала наложен шум

y{t)=xi + e

"езащУ"" оценки скорости при тех же самых значениях К, что и для случая "осятся"" Рний, показан на рис. 3.20. График показывает, как соот-УЖе ""Ходимость и точность оценки. При малых значениях К сходимость Итоговая точность вполне приемлема. Большие значения К позволя-

ют получить быструю сходимость, но общая точность оценки неудовлет тельна. Очевидно также, что оценка скорости дифференцированием упа"" ворота вала будет давать очень плохой результат. "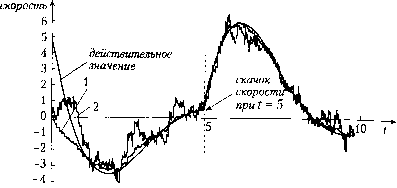

Рис. 3.20. Оценка скорости при измерении угла поворота в условиях шумов; сходимость для варианта 2 быстрее, но выше чувствительность к возмущениям. Значения вектора оценки К такие же, что и для примера на рис. 3.19: 1 - iCi = 3, X, = 3-2-iiCi =3,72= 15 i г

Для того чтобы найти наилучшие значения вектора К при зашумленных измеренюх нужно использовать более сложные методы. Наилучшие значения К часто изменяются в зависимости от времени. Они могут быть достаточно большими до тех пор пока разность между реальным измерением y(kh) и его оценкой Sikh) = С х(Й! больше, чем e(kh). Когда погрешность уменьшается и ее значение становится соизмеримым с шумом e(kh), то и значения К следует соответственно уменьшить.

На переменные состояния могут влиять возмущения, которые нельзя смоделировать детерминированным образом. Для учета влияния ошибки моделирования и* шумов процесса в разностное уравнение (3.9) добавляется член, характеризуют* возмущения. Типичным примером является измерение уровня жидкости в больн"" емкости с волнением на поверхности, которая вызывает случайные колебания изм ряемого уровня. Другим примером может служить измерение момента электрол<°° ра, при котором возникают небольшие пульсации из-за работы преобразователя тоты. Такие отклонения можно моделировать случайными величинами v( которые добавляются к уравнению состояния

х[(к+1)Ь]=Ф- x{kh) + Г u(kh) +v(kh)

Эти случайные величины могут быть учтены аналогично измерительному шУ- В этом случае регулятор учитывает неопределенность и его действия УДУ,, "осторожными", т. е. коэффициент усиления регулятора должен быть °ri„j

Оптимальное значение К зависит от типа возмущения. Фильтр Калмана (а filter) - это функция со структурой, соответствующей уравнению (3.20), и щаяся на описании системы уравнениями (3.19) и (3.21). Значение К, получае> фильтра Кальмана, изменяется во времени и представляет собой оптимальный ромисс между возмущениями в системе и в датчиках и погрешностью оценки.

неопределенное 113

здсистем-S:---

-2 нечеткие системы З-" только нелинейны и нестационарны (изменяются во време-

Многие сист определены. Их нельзя смоделировать уравнениями или ни). и° бором ясных логических правил типа "если-то-иначе". Для решения

представить на американский ученый Лотфи А. Задех (Lotfi А. Zadeh) разработал подобных (fuzzy logic). Термин "нечеткая" фактически использован не совсем

нечеткую °у логика прочно базируется на математической теории, правильно, п можно рассматривать как методологию дискретного управле-

Нечетку человеческое мышление, с использованием такого свойства, н„я, физическим системам, как неточносты В традиционной логике и

"" слительной технике используются детерминированные множества, т. е. всегда можносказать, принадлежит ли элемент множеству или нет. Обычная - бинарная -вдгика оперирует только противоположными состояниями - "быстро/медленно", "открыто/закрыто", "горячо/холодно". В соответствии с этой логикой температуру 25 °С можно расценить как "горячо", а 24.9 °С - еще "холодно", и регулятор температуры будет реагировать соответственно.

В противоположность этому нечеткая логика работает, преобразуя жесткие двоичные переменные - "горячо/холодно", "быстро/медленно", "открыто/закрыто" - в мягкие градации с изменяемой степенью принадлежности (degree of membership) - "тепло/прохладно", "довольно быстро/несколько медленно". Температура 20 °С может означать одновременно и "тепло", и "прохладно". Такие градации игнорируются обычной логикой, но служат краеугольным камнем нечеткой логики. Степень членства определяется доверием (confidence) или уверенностью (certainty) (выражается числом от О до 1), что конкретный элемент принадлежит нечеткому множеству.

Нечеткие системы вырабатывают свои решения на основе входной информации в форме лингвистических переменных, т. е. терминов обычного языка, например "горячо , медленно" или "темно". Эти переменные обрабатываются правилами "если-того"" результате формируется один или более выводов в зависимости от ствщГс* ™*" истинны. Вывод каждого правила взвешивается в соответ-

с доверием или степенью принадлежности его входных значений. 1еллектаТ- "°°Р аналогия между правилами "если-то" искусственного ин-лект "telligence - AI) и нечеткой логикой, хотя искусственный интел-BHTerne.g°i Рботки символов, а нечеткая логика - нет. В искусственном структур ""Р°""я сеть есть совокупность данных и выводов в виде специальных ой коэфгК входной величине назначается относительный, дискретный весо-ьдля прщ"*" збшенные данные точно определенным способом формируют ""Рерывно " решений. В отличие от этого в нечеткой логике весовые функции

*четкая°"" множестве значений принадлежности, ч "змеряю-сТу часто имеет дело с переменными, которые скорее наблюдаются, " Отличие п правление на основе нечеткой логики имеет еще одно существен-"ели системь"""° традиционным. Последнее основано на математической """epegjj торая предполагает наличие детальных знаний о соответствую-jl" "од/в Моделирование на основе нечеткой логики имеет дело с отношени-

ij" Замена б ° *°°Р собраны вместе многие параметры. При таком управле-Наптт. ольщого

адлр-.,, •"ьщого *"остипомо

диапазона значений на меньшее количество градаций

гает сократить число переменных, которыми должен опериро-