Пример 5.6

фильтр низкой частоты второго порядка

ФНЧ второго порядка (рис. 5.18) имеет две независимые частоты среза и/с2-

Vi с-[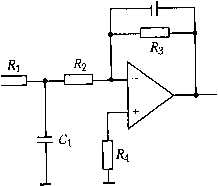

о Vn

Рис. 5.18. Фильтр низкой частоты второго порядка Частотно-зависимый коэффициент усиления

GO«)l =

«1 + 2

R: Ro

2л (J?, + Ro) Cj

Если частоты среза совпадают (J = /1 fcl) ™

i?3 1

[Гц]

G1 =

1 +

При частоте входношсг уменьшается в двараза

/ D *+.,..-r„MZ) йНрг имеет постоянную частотную sasncHN ФкльтоВаттерворта (BuUerwortnfilter) 1лмсс j , .ToBef

1Уилырос11. н F \ji„3CT0Tb[/а. Благодаря тому что этот фильтр

тяюший псевдочастоты. Фильтр Баттерворта можно считать частным случаем

а Саллен-Ки (Sallen-Key filter). Вариант этого фильтра второго порядка пока-

г,ис. 5.19. Параметры элементов фильтра Баттерворта должны удовлетворять зан на и соотношениям

2я-К-С1-/о= V2"

2я-7?.С2-/о = -2-

фильтры более высокого порядка (4, 6,...) представляют собой.жаскадное,соединение фильтров второго порядка.

Vi о-

-О Vn

Рис. 5.19. Фильтр низкой частоты второго порядка с единичным коэффициентом уси-.тения ~ фильтр Саллен-Ки

5.3.3. Фильтры высокой частоты

Очевидно, что, поменяв местами конденсатор и резистор в схеме рис. 3.4 или индуктивность и резистор в схеме рис. 5.17, в результате получим фильтры высокой частоты (ФВЧ, high pass filter) (рис. 5.20).

Ис. 5.20. Пассивный 7?С-фильтр высокой частоты (а) и пассивный Д1-фильтр высо-ои частоты ((J) ч и

*ецл"°" преобразования, что и в примере 3.4, получим следующее выра-Для выходного напряжения Vg высокочастотного jRC-фильтра

dv dt

(5.6)

Глава 5. 06pii«№a сигна 3 дз1пговая фильтрация

тд.еТ= R-C. Передаточная функция имеет вид

G(5) = -

V,(s) 1 + sRC i + s-T Частотно-зависимый коэффициент усиления фильтра

(5./,

ju>RC

1 + jwR-C

RC

Ji + ((x)RC) Vl + (CO • Tf

Такая схема будет задерживать низкочастотные и пропускать высокочастотные сигналы, как показано на частотной характеристике (рис. 5.21).

частота среза

logvo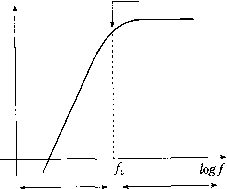

подавляемые частоты

пропускаемые частоты

Рис. 5.21. Частотная характеристика фильтра высокой частоты первого порядка Частота среза/,., при которой ослабление амплитуды составляет {2, определяйся выражением

2n-R-C

Коэффициент усиления по напряжению

2п-Т

[Гц]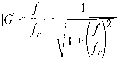

(5.8)

Так же как и низкочастотный фильтр, активный высокочастотный филь Р построить на основе операционного усилителя с обратной связью (рис 5-

Частотно-зависимый коэффициент усиления по напряжению активного Ф,, высокой частоты есть отношение импеданса обратной связи к входному им

\G(j)\ =

-jo) R2- С

1 +;(0 Ry С

(а R2- с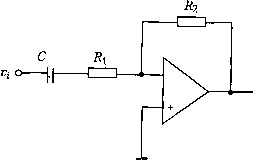

Рис. 5.22. Активный фильтр высокой частоты первого порядка

Поскольку все операционные усилители имеют офаниченную полосу пропускания, коэффициент усиления уменьшается по мере повышения частоты. Строго говоря, все активные высокочастотные фильтры на самом деле являются полосовыми фильтрами, поскольку обеспечивают усиление сигналов в определенном частотном диапазоне, ослаб-ляя сигналы, лежащие соответственно выше и ниже фаничных частот.

Пример 5.7

Пассивный RL-фильтр высокой частоты

Пассивный фильтр высокой частоты, показанный на рис. 5.20, (5 определяется дифференциальным уравнением, полученным на основе второго закона Кирхгофа

dr>u dt

которое идентично уравнению (5.6), если положить Т = L/R tro передаточная функция

G(s) =

ад sL

K,(s) R + s-L i+s-T частотно-зависимый коэффициент усиления

"Частота среза

F,Oa))

JO) • L

(R +7(0 • L)

i + Ш

2n-L 2пТ

[Гц]

это выражение для/,, коэффициент усиления по напряжению мож-

!!!£Зьаналогично уравнению (5.8).

5.4. Цифровая фильтрация

После аналоговой фильтрации, АЦ-преобразования и ввода данных в компью выполняется цифровая фильтрация. Цифровая фильтрация обладает большой гц костью, поскольку характеристики фильтра можно изменить, просто задав новыед раметры соответствуюшей ему программы. В отличие от аналоговых, цифро фильтры хорошо работают с длительными постоянными сигналами.

5.4.1. Общая структура цифровых фильтров

В общем виде цифровой фильтр (digital filter) можно представить как y(kh) = -flj • y[(k - i)h] ~ «2 • y[(k - 2)h] - ... - «„ y[(k - n)h] + + bQ-y(kh) + ... + b,„-y[(k--m)h

(5.9)

где/г - это интервал выборки, г/" - отфильтрованный выход, - вход. Заметим, что аргумент kh, по смыслу представляющий из себя время, можно рассматривать и просто как номер (k) в последовательности входных значений. Если все коэффициентыа равны нулю, то такой фильтр называется фильтром скользящего среднего (Моащ Average ~ МА) с конечной импу.пьсной характеристикой. Это означает, что если в течение некоторого времени все последовательные значения yj, кроме одного, равны нулю, то на выходе фильтра сигнал будет отличен от нуля только на т временных интервалах. Если некоторые либо все коэффициенты не равны нулю, то такой фильтр называется авторегрессивным (AutoRegressive - AR) и имеет бесконечную импульсную характеристику. Другими словами, входной сигнал, отличающийся от нуля только на одном временном интервале, вызовет появление на выходе сигнала отличного от нуля в Течение бесконечно долгого времени. Обобщенный фильтр, описываемый уравнением (5.9), называется авторегрессивным фильтром скользящего среднего (AutoRegressive Moving Average - ARMA).

Фильтры могут быть "причинными" и "непричинными". Причинный (causal фильтр вычисляет выходное значение на основании ранее введенных данных (в люоо! момент tQ учитываются входные значения только для t < t). Поэтому все фильтр» реального времени (on-line) являются причинными. Последовательность отфиль рованных значений на выходе будет отставать на некоторое время по сравнению с п следовательностью на входе. Если данные обрабатываются в автономном режну (off-line), например при анализе серии значений уже собранных измерений, мо** использовать непричинный (non-causal) фильтр. В этом случае расчет для мом* времени можно производить на основе как предыдущих (t<tff), так и следующих (t > tQ) значений.

5.4.2. Цифровые фильтры низкой частоты

Для того чтобы исследовать медленно изменяющийся входной сигнал, необхо мо удалить из измерительных данных случайные пики и высокочастотные наво". которые не содержат какой-либо полезной информации. Это можно сделать с по щью цифрового фильтра низкой частоты (digital lozo pass filter). Структура ЦифР°1), го фильтра, который эффективно удаляет резкие колебания сигнала и в то же вр. не влияет на медленные изменения, всегда компромиссна, потому что частотнЫ апазоны исходного и постороннего сигналов обычно пересекаются. Как и у ана."

д,а наиболее важных типа ФНЧ - скользящего среднего и экспоненциальногп

еглаживания(..;.оп.п.г./5™о.Лш).ФНЧ,используемыевпромыщдеГосГп" зсегда базируются на одном из этих простых фильтров. ленности, почти

Пример 5.8

фильтр скользящего среднего - простейший ФНЧ

Простой фильтр скользящего среднего получается, если принять все параметры а,- в уравнении (5.9) равными нулю. Если необходимо простое усреднение, то все весовые коэффициенты й- равны и дают в сумме единицу. Например, фильтр скользящего среднего с пятью входными отсчетами имеет вид

y(kh)--{y(kh)

y[(k-4)h])

Если операция фильтрации производится не в режиме реального времени, то величину скользящего среднего можно подсчитать, используя измерения как до, так и после заданного момента времени kh. В этом случае отфильтрованное значение не отстает по времени относительно входных значений. Непричинный простой фильтр скользящего среднего по пяти значениям имеет вид

y(kh)---[y[(k-2)h] + ...+y[(k + 2)h

Если величина на выходе представляет собой усреднение по последним п выборкам, то она смещается на 1 + п/2 циклов. При больших значениях п выходной сигнал становится более гладким, но при этом все больше отстает по времени. Импульсная характеристика фильтра скользящего среднего конечна. Для входного импульса в момент t = О выходной сигнал после момента t = п становится нулевым.

Скользящее среднее - это простой метод, но он имеет определенные ограничения. При использовании одинаковых коэффициентов фильтр может быть излишне инертным и недостаточно быстро реагировать на реальные изменения во входном сигнале. С другой стороны, если коэффициенты различны и убывают

:!льших значений

индекса п, то это затрудняет анализ свойств фильтра.

сц,""нциальный фильтр (exponential filter) - это авторегрессионный фильтр зящего среднего первого порядка, определяемый следующим уравнением

y(kh)=a-y[(k-i)h] + (i-a)-y(kh) (5.10)

Нцд Рванное значение y(kh) вычисляется суммированием предыдущего значе-ito,.Q "-"трованного сигнала [( - 1)] и последнего значения y(kh) измеритель-•У О с весовыми коэффициентами. Коэффиттирнт п гтр-аггд-г п ,л.т.„,т,., Уравнение (5.10) можно переписать в вид.

ициент а лежит в интервале межвиде

г (5.10) можно перепи y(kh) y\(k - i)h] + (i - а) [у{Щ -~у[(к~\)h])