«l«« + ll"l + - + lr"r

- = + ... + a„„x„ + bu + ... + bu

где параметры aj и by - константы. Поскольку эти уравнения являются дифференциаль-ными уравнениями с постоянными коэффициентами, они обладают рядом привлекательных свойств. Например, всегда можно найти аналитическое решение x(t) при произ. вольных входных сигналах и(). Начальные условия определяются п константами

х(0) = (.гю ... x„q) В матричном виде уравнения состояния записываются значительно проще

- = А х + В U

где А и В - матрицы, содержащие постоянные коэффициенты

(3.1)

При единственном управляющем сигнале матрица В имеет только один столбец.

Между внутренними переменными состояния х и измерениями у существует линейная зависимость. Кроме того, иногда имеется прямая связь между управ.пяющи-ми переменными и и выходными переменными у

г/1 = СцХ! + ... + ci„ + du + ... + й?1

Ур = Ср1\ + •- + Српп + р1"1 + - + или в векторно-матричных обозначениях

(3.2)

Если имеется только одна выходная переменная, то С состоит из одной строки-Обычно нет прямой связи между входными и выходными переменными, и тогда ма- рица D - нулевая.

Линейная система имеет много преимуществ (сравните, например, с некоторым свойствами нелинейных систем, упомянутыми в разделе 2.2.7). Наиболее важныМ

йством линейных систем является принцип суперпозиции (supeiposition principle). означает, в частности, что если при каком-либо изменении амплитуды входного Тната Аи выходной сигнал изменится на величину Ау, то при удвоенном изменении ""ОДНОГО сигнала 2 • Аи выходной сигнал изменится на величину 2 Ау.

Линейные системы обладают свойством аддитивности входных сигналов, т. е, ес-входной сигнал и вызывает выходной сигнал z/j, а 2 - сигнал г/2, то общий сигнал и -I- 22 на входе приведет на выходе к z/j -ь г/2. Как следствие, влияние сигналов правления и возмущений можно анализировать отдельно.

Несмотря на все достоинства линейного описания, применять его следует с большой осторожностью, поскольку большинство технических процессов существенно нелинейны. Если нелинейности "гладкие", т. е. отсутствуют скачки, то при определенных условиях нелинейную систему можно рассматривать как линейную. Тогда линейное описание справедливо для малых отклонений вокруг точки равновесия.

Многие параметры промышленных процессов должны поддерживаться вблизи некоторых постоянных - опорных - значений; целью систем управления является приведение параметров процесса к их опорным значениям. Пока отклонения от опорного значения малы, линейное описание является адекватным. Однако при больших отклонениях могут потребоваться более точные модели, поскольку влияние нелинейности будет существенным.

v3.3.4. Описание в виде отношений входных и выходных переменных

Частотные методы (пример 3.4 и раздел 3,3.1) используют анализ функций комплексной переменной и преобразование Лапласа. Главные элементы этого подхода - передаточные функции, функциональные блок-схемы и их преобразование, анализ нулей и полюсов, К преимуществам анализа систем в частотной области относится возможность собрать соответствующие экспериментальные данные, позволяющие непосредственно построгп-ь удовлетворительную модель системы. Из-за этого метод частотных характеристик обычно используют при описании сложных систем, например усилителей с обратной связью, а также многих электромеханических устройств и систем.

Если описывается только связь между входными и выходными сигналами, то некоторые внутренние переменные и их взаимосвязи остаются скрытыми, представление системы становится более компактным и имеет меньшее число параметров, чем сание в пространстве состояний. Поскольку в модель включены только входные 8 пп переменные, то она называется внешним описанием (externaldescription) perv """•""ость внутреннему представлению уравнениями состояния. Многие одеТ™ ""Р""? ПИД-регулятор, описанный в главе 6, настраиваются на базе

и технического процесса в виде отношений входных и выходных переменных. НИР г. "УРннего описания системы можно исключить вектор х и получить описа-

системы в виде

d dt„

у , л d-h

+... + й„г/ = йо-т- + Й1-- -1 dt„ dt„

--(-... + й w

Сог°**Ц""ты Я; и й,- могут быть получены из матриц А, В, С и D. В системах со -ми входными и выходными переменными для каждой пары вход/выход суще-

Глава 3. Описание и моделирование сирт.

ствует своя зависимость (в дальнейшем рассмотрение будет ограничено система, только с одним входом ии одним выходом у). Для дифференциального уравнед порядка п можно выполнить преобразование Лапласа

(5" + «1 • 5"-1 + ... + а„) 7(5) = (Ьо s" + b- s" + ... + й„) • U(s)

где 5 - переменная Лапласа, а F(s) и U(s) - результат преобразования Лапласа (изо ражение) для y{t) и uit) соответственно. Преимущество этого метода в том, что щ плексными переменными s, которые представляют собой операторы дифференцир вания, можно манипулировать алгебраическими методами. Здесь полагается, чк начальные значения переменных состояния - нулевые.

Связь между входными и выходными переменными линейной системы .мож выразить ее передаточной функцией {transfer function), которая определяется Kai отношение между изображениями Лапласа выходного и входного сигналов систещ

G{s) =

Y{s) bs" + bs"- + ... + b U(s)

s„ + + ... + a„

(3,3

Передаточную функцию также можно рассчитать непосредственно из внутреннег описания в переменных состояния [уравнения (3,1) и (3,2)], Имеет*место следующе, соотношение

Y(s)

G(s) =-= С • (Л - А)~ В + D

U(s)

(3,i

где I - единичная матрица порядка п. Вывод этого выражения очень прост и приво дится в большинстве книг по управлению. В системе с одним входом и одним выхо дом матрица С состоит из одной строки, а матрица В - из одного столбца, матрицаЛ имеет размерность и X и. Обычно матрица D (имеющая при этом размерное!» 1 X 1) - нулевая, В этом случае G становится скаляром. Для нескольких входов» выходов G(s) является матрицей с элементами Gy(s), которые суть передаточнм функции для каждой пары вход м,- и выход г/.

Примерз.12

Передаточная функция механической системы

Передаточная функция системы из примера 3.2 (раздел 3.2.1) имеет вид

Z{s) 1

G(s) =

F(s) ms

где Z(s) и F(s) - изображения Лапласа для координаты z и силы F соответственно. Уравнения состояния были получены в примере 3.11. Передаточную функцию можно также вычислить непосредственно из уравнений состояния [см.уравнение (3.4)]

g(5) = C-(5l-А)--В = (1 0)

/ о

Непрерывные модели динамических систем

примерз.13

низкочастотный фильтр

Низкочастотный 7?С-фильтр из примера 3.4 можно характеризовать его пе-аточной функцией. В предположении, что начальные напряжения равны нулю, связь вход/выход можно записать как

G{s) =

У; (5) \+sR-C

Изменение амплитуды выхода и фазовый сдвиг для синусоидального сигнала получаются при замене в передаточной функции 5 на jo.

Поскольку описание вход/выход содержит меньшее число коэффициентов, чем внутреннее описание в пространстве состояний, то его всегда можно получить из последнего; однако обратное преобразование неоднозначно. Это совершенно естественно, так как вектор состояний х получается с помощью подстановки в исходные уравнения новых переменных, которые можно выбрать произвольно, а у и и зависят от физической природы процесса и поэтому определены однозначно.

Знаменатель передаточной функции называется характеристическим уравнением {characteristic equation). Корни характеристического уравнения называются полюсами {poles) и имеют фундаментальное значение. Значения полюсов идентичны собственным числам матрицы А, Корни числителя передаточной функции называются нулями {zeros). Если нули обозначить Zj, „„ z, а полюса - .....р, то при п>т

передаточную функцию (уравнение 3,3) можно записать в виде

G(5) =

K-{s~z)-{s-zJ «1

+ ,„ 4-

{s~p)-{s-p) s-p sp„

где a - действительные или комплексные константы. Это означает, что выходную переменную г/ можно представить суммой показательных функций, которые называются составляющими движения или модами {modes)

y{t) = • e-Pr- + ... + c„ е~РпЧ [слагаемые, зависящие от u{t)\

степе"™ соответствует слагаемому с вещественным показателем nrm комплексно-сопряженных полюса всегда можно представить в виде одного слагаемого.

Если два полюса имеют значения

то . =-о±;«

этой паре соответствует слагаемое передаточной функции

• е"° • sin(oj/;)

Деляют* """ собственные числа матрицы А) линейной системы полностью опре-"Ция Устойчивость, Если вещественные части полюсов - отрицательные, то ре-тойчи °Р2"иченный входной сигнал и также всегда ограничена, т, е, система ус-

Нули определяют значения коэффициентов экспоненциальных функций в о-,, клике, но при этом не влияют на устойчивость системы. Если полюс располагаете, близко к нулю, то соответствующая мода мала. Если полюс и нуль совпадают, мода исчезает.

3.3.5. Область применения линейных моделей

Существуют динамические явления, которые нельзя описать линейными дифф. ренциальными уравнениями с постоянными коэффициентами. Рассмотрим влияни; нелинейности на примерах. Системы, описываемые ниже, ведут себя как линишьк при малых значениях входных сигналов, а при больших - появляется нелинейность.

Примерз.14 Ограничения сигнала

В реальных условиях все сигналы ограничены. Во многих технических системах в качестве конечных управляющих элементов используются клапаны. Поскольку клапан не может быть открыт больше, чем на 100 %, рассчитанный математически сигнал управления иногда просто нельзя реализовать (рис. 3.14). Это вызывает определенные трудности в управлении, обсуждаемые в главе 6.

Другой пример ограничения сигнала - ток ротора электрического двигателя. Ток должен быть ограничен, иначе двигатель сгорит. Соответственно, система управления двигателем не может быть линейной, особенно при больших ускорениях и моментах, когда ток тоже должен быть большим.

выходной сигнал, у

входной сигнал и

Рис. 3.14. Выходной сигнал исполнительного механизма с ограничениями

Пример 3.15

Процесс аэрации

Рассмотрим снова станцию аэрации сточных вод (пример 3.8, раздел 3.2.3). Для процесса аэрации принцип суперпозиции не выполняется. Предположим, что входной поток воздуха и и скорость поглощения кислорода R не меняются.

концентрация растворенного кислорода поддерживается постоянной около точки равновесия со значением равным 3 мг/л.

На рис. 3.15 показано, что когда входной поток изменяется скачком (2 %, 4 % и т.д.), концентрация достигает нового стационарного значения за час. II и изменении расхода воздуха шА% изменение концентрации практически точно вдвое превышает изменения концентрации по сравнению с 2 % изменения расхода воздуха. При этом обе кривые симметричны относительно точки равновесия. Однако уже при 8 % изменения расхода воздуха очевидна асси-метрия в реакции системы. При изменении расхода на ± 20 % изменения в концентрации уже существенно несимметричны и, более того, не в пять раз отличаются от изменений, вызванных 4 % изменения расхода. Приведенные кривые иллюстрируют практическое проявление нелинейности.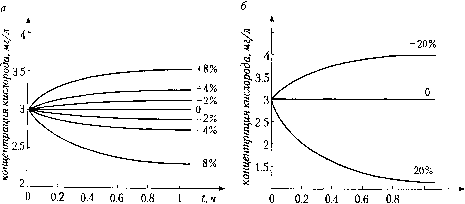

1 t,4

Рис. 3.15. Изменение концентрации растворенного кислорода в баке аэрации при скачке расхода воздуха (входная переменная) в момент времени i = 0. Результаты приведены для значений входной переменной: ±2%, ±4%и±8% (й); + 20 % {б)

Системы, описанные выше, имеют "слабые" нелинейности, т. е. ведут себя практически линейно при малых значениях входного сигнала. Многие системы при больших отклонениях от точки равновесия требуют более точного описания, чем линейные дифференциальные уравнения, поэтому необходимо добавлять нелинейные слагаемые. При моделировании должны быть четко определе-J;JTaHHribiB рамках которых линейное описание является адекватным.

••6. Нелинейные системы

опуп °ннные в разделе 3.3.5, являются нелинейными, но при некоторых 1елин ™ можно аппроксимировать линейными уравнениями. Другие типы прим*"° нельзя свести к линейному описанию. Наиболее часто встречающий-ено/в ~ релейные системы. Реле вырабатывают бинарные сигналы типа "вклю-еетф""*""" •"ьное реле для любого положительного входного сигнала ЧЦат "РОииьш положительный выход и, соответственно, фиксированный от-Не Вы "й выход при любом отрицательном входе. Очевидно, что в такой системе нолняется принцип суперпозиции.