Greg

регулятор

внешнее возмущение

технический процесс

Рис. 6.2. Структура простейшего регулятора

С математической точки зрения передаточная функция Gjg{s) рассматриваем точно так же, как любая передаточная функция процесса G(s). Как уже упоминалос их принципиальное различие в том, что коэффициенты передаточной функции реп лятора Gjq{s) можно изменять (настраивать). Проектировщик системы управления должен подобрать эти параметры так, чтобы замкнутая система - физически процесс и регулятор - работала в соответствии с установленными требованиями Замкнутая система, изображенная на рис. 6.2, имеет передаточную функцию

Gcis) =

ns) Сигс() G(5)

UAs)

(6,3)

1 + Gj,Eds) G(s)

Очевидно, что чем больше параметров содержит Gj£q(s), тем больше степеней свободы имеет регулятор. Настраивая эти параметры, поведение передаточной функции замкнутой системы можно при желании изменять в достаточно широких пределах. В дальнейшем обсуждается уровень сложности регулятора, необходимый для достижения заданных характеристик.

6.3.2. Упреждающее управление по опорному значению

Простейшая система управления, показанная на рис. 6.2, реагирует только на ошибку e(t) и не использует по отдельности два входных сигнала - опорное значе и выходной параметр процесса.

Однако ошибка может возникнуть по двум причинам, одна из которых -ние опорного или задающего сигнала u(t), а вторая - изменение нагрузки или кое-либо другое возмущение в системе, вызывающее изменение выходного си y(t). Изменение опорного значения - это известное возмущение. Если регулятор жет использовать соответствующую информацию, то это, вообще говоря, ".jop-улучшить характеристики замкнутой системы - физический процесс и регУ-" В этом смысл упреждающего управления (feedforward control). x

Рассмотрим регулятор [уравнение (6.4)], состоящий из двух частей. Контур ной связи Gf{s) представляет собой исходный регулятор, отрабатывающий оШ Так называемый контур упреждения Gjis) контролирует изменения опорного ния и прибавляет к управляющему сигналу поправочный член, с тем чтобы вся сИ реагировала более оперативно на изменения опорного сигнала (рис. 6.3). То ест равляющий процессом сигнал U{s) представляет собой сумму двух сигналов

Рис. 6.3. Регулятор, содержащий контур упреждающего управления по опорному значению и контур обратной связи по выходу процесса

U(s) = Gpp(s) U(s) + Gpj(s) [U,(s) - Y{s)]

Это выражение можно переписать в виде

Uis) = [Gpfis) + GpBis)] U,(s) - Gps(s) Y(s)-

= Gpis) U,(s) - Gj,(s) Y(s) = Up(s) - UpB(s)

(6.4)

где - упреждающий сигнал по опорному значению (задающему воздействию), а Upg - сигнал обратной связи. Регулятор имеет два входных сигнала UJs) и Y{s) и, следовательно, может быть описан двумя передаточными функциями Gpfs) и Gp{s) (рис. 6.4).

технический процесс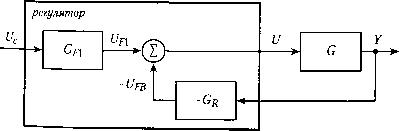

связью "УР линейного регулятора с упреждающим управлением и обратной

Посколь

"°До%и.°5"°в м простейший регулятор уравнения (6.3), разумно пред-

тьку регулятор, соответствующий уравнению (6.4), имеет больше настраи-

*Кцио замкнутая система имеет лучшие характеристики. Передаточную полного контура управления можно получить из рис. 6.4

{Gpis) U(s) - Gj(s) Yis)] G(s) - Y(s) ение можно преобразовать следующим образом

Y(s) Gp(s) G(s)

Gc(s) =

,"°Лож

U,(s) 1 + G(s) Gjiis)

(6.5)

Чятор Q полюсов системы с обратной связью можно изменить с помощью ре-й(-5), а упреждающий регулятор Gp(s) добавляет системе новые нули. От-

Глава 6. Структурьрр

сюда следует, что вся система может быстро реагировать на изменения опорног нала, если Gp(s) выбрана должным образом. г-

6.3.3. Обобщенный регулятор

Благодаря тому что в упреждающем регуляторе опорное значение непреп отслеживается, возможно создание высокоточных (серво) систем управления э роприводами, роботами или станками. Для этих приложений важно, чтобы реак на выходную величину процесса была быстрой и точной при любых изменен опорного значения.

Описание регулятора можно обобщить еще больше. Если числитель и знамена тель передаточных функций GJ(s) и Gfi(s) уравнения (6.4) выразить полиномами от s, то описание регулятора можно представить в следующем виде

Uis) - Gp,is) (/,(s) - G(s) F(s) = • U(s) -

l(s) 2()

5i(5)

Y(s)

Две части управляющего сигнала показаны на рис. 6.4. Приведя передаточные функции к общему знаменателю, получим

Цз) S(s)

R(s) R(s)

где R(s) = R(s) R2(s), T(s) = T(s) i?2(5), 5(s) = 5(з) R(s). Последнее можно переписать как

(6.6)

U(s) =

ri-"-!+ ... + ?„

Vis)

где r,-, 5j и tj - параметры передаточных функций, as - комплексная переменная преобразования Лапласа.

Таким образом, регулятор, соответствующий уравнению (6.6), можно предст вить в виде обобщенного регулятора (general controller)

R(s) U(s) = T(s) U(s) - S(s) Y(s) Передаточную функцию физического процесса можно явно выразить через числитель и знаменатель

(6.7)

G(s) =

bo-s» + by s"~ + ... + b„

B(s) Ais)

Замкнутая система, приведенная на рис. 6.5, соответствует рис. 6.4. Используя выражения (6.6) для регулятора и (6.8) для физического процесса, редаточную функцию замкнутой системы можно записать в следующем виде

T(s) 5(s)

Y{s) R(s)A(s) T(s)-B(s) (6

G,(s)-----= --

B(s) S(s) A(s) R(s) + B(s) S(s) A(s) Ris)

овьюрегуляторы

Uc(s)

Рис 6.5. Регулятор, содержащий контур упреждающего управления и контур обратной связи (этот регулятор соответствует рис. 6.4)

Передаточная функция замкнутой системы имеет много степеней свободы. Коэффициенты полиномов A(s) и B(s) зависят от процесса и поэтому не могут изменяться. Некоторые из этих коэффициентов бывают неизвестны, а их оценка достаточно сложна. Получение точной модели системы является нетривиальной задачей! С другой стороны, все параметры полиномов R(s), S(s) и T(s) можно подбирать. Коэффициенты T(s) и R{s) относятся к части регулятора, осуществляющей упреждающее управление. Настройка этих параметров определяет реакцию замкнутой системы на изменения опорного значения. Аналогично, коэффициенты полиномов S(s) и R(s) определяют характеристики контура обратной связи. Настраивая S(s) и R(s), можно влиять на реакцию регулятора при изменении нагрузки или любом другом возмущении, вызвавшем изменение выходного сигнала г/(0.

Для вычисления параметров регулятора передаточная функция [уравнение (6.8)] обычно сравнивается с некоторой целевой передаточной функцией

Gm(s)=

y(s) BJs)

U,(s) A„(s)

Параметры полиномов R(s), S(s) и T(s) можно выбрать при этом таким образом, что

BJs) = T(s)B(s)

A,(s)=A(s)-R(s) + B(s)-S(s)

lecTB" " "- имеют достаточно высокий порядок, т. е. достаточное коли-Hjjg-ggPyeK настройки", передаточную функцию замкнутой системы [уравне-аким °жпо изменять в широких пределах. Порядок регулятора п должен быть ожно* исходного физического процесса. В частности, подбирая R(s) и 5(5), Teopg.lJ"" менять знаменатель передаточной функции замкнутой системы. Место " то означает, что полюса замкнутой системы можно сдвинуть в любое Менец°""""° плоскости. На практике максимальные амплитуда и скорость из-Ра.зде управляющего сигнала ограничивают свободу перемещения полюсов. Khcj* •3-4 бьгпо показано, как полюса влияют на тип переходной характеристи-ByiQ J и позволяют произвольно выбрать ее динамику. В частности, неустойчи-о*н систему, имеющую полюс с положительной вещественной частью,

о Стабилизировать с помощью системы управления.

Глава 6. Структуры

Пример 6.1

Управление положением вертикального стержня

Стержень, установленный вертикально на опоре, в реальных условиях может находиться в таком положении сам по себе и упадет, если не предприн мать некоторые меры для его поддержки; такой стержень представляет собо" неустойчивую систему. Если нижний конец стержня непрерывно перемещать в горизонтальной плоскости так, что стержень сохраняет вертикальное пото жение, то система становится устойчивой. На языке теории управления это означает, что стержень имеет полюс с положительной вещественной частью. Pg. гулятор (человек или автомат) имеет динамику

S(s) R(s)

такую, что все полюса полной системы (стержень и регулятор) имеют отрицательные вещественные части.

В разделе 3.3.4 также описано влияние нулей на относительную величину отдель ных членов переходной характеристики. Хотя изменить расположение нулей нельзг их можно сокращать, вставляя полюс в то же самое место, а также вводить новые тж

Нули числителя в уравнении (6.9) совпадают с нулями полиномов T(s) и j5(s).Ht вые нули можно добавить с помощью полинома T(s). Однако нули B(s) фиксирован; и переместить их нельзя. Лишь в случае размещения полюса на том же месте нол; сокращается. Однако такие действия требуют осторожности. Например, если нол; полинома B(s) размещен в правой полуплоскости - такая система называется нами-нимально-фазовой (non-minimum phase system), - то и сокращающий его полюс ,io жен быть помещен также в правую полуплоскость. Это приводит к неустойчивое системы, но точный выбор нуля исключает неустойчивую составляющую движен11 Однако если сокращение производится неточно, как это обычно бывает, то замкь; тая система окажется неустойчивой, т. е. не каждая математически корректная рация приводит на практике к желаемому результату. Иными словами, если ф ческая система имеет ноль в правой полуплоскости, то это отражает cboi системы, которое нельзя устранить с помощью регулятора. Однако влияние свойства можно уменьшить соответствующим выбором структуры управления

Неминимально-фазовые системы характеризуются поведением, которое в тором смысле противоречит ожидаемому, обычно из-за определенного запазды ответа. Пример неминимально-фазовой системы можно заимствовать из экoнo На рис. 6.6 показана кривая прибыли от продукта в течение его жизненного На ранней стадии, до начала продаж, капитальные вложения и стоимость про вания приводят к отрицательной прибыли (издержкам). По прошествии некот времени - будем надеяться - продукт начинает приносить прибыль. Это лежит в природе вещей и не может быть изменено. Однако руководитель, е будет действовать как очень простой регулятор, оценив текущее значение пР"р,г может принять решение об остановке работ в самом начале, поскольку прибыль . цательна. Из этого примера видно, насколько важно предвидеть будущий усп „ni дукта для продолжения работы. Регулятору, управляющему неминимально-

рговыерегуляторы

opi, требуется такое же свойство, поскольку он должен каким-либо о едсказывать будущее поведение системы и действовать соответственно.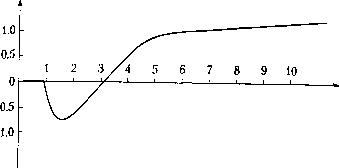

время

рис. 6.6. Прибыль в течение жизненного цикла продукта. Вначале затраты на npi тирование и капитальные вложения приводят к издержкам. Любое управляющее; действие, предпринятое на основе оценки мгновенных значений без учета хода i кривой, будет ошибочным

Полиномы R(s), S{s) и T(s) нельзя выбрать произвольно. Все передаточные ции регу.пятора (рис. 6.5) должны быть реализуемы физически. Это означает, ч пень знаменателя должна быть выше степени числителя, т. е. порядок R(s) долж( восходить порядок как S(s), так и T(s), в противном случае реальный регулятор с невозможно. Сам физический процесс должен быть управляемым (раздел 3.5.1 ] означает, что A(s) и B(s) не могут иметь общих множителей.

Существуют также другие ограничения, связанные с тем, насколько можно "ить параметры регулятора. Если "ручки настройки" крутить слишком интеш например многократно уменьшая время реакции процесса, то управляющие си огут войти в зону насыщения и система перестанет быть линейной. Иными < ли, из-за ограниченности амплитуды сигналов реакцию замкнутой системы г изменить произвольным образом.

•4. Упреждающее управление по изменению нагрузки и возмущению

в при" возмущения, действующие на процесс, известны и их можно измерн выхо а ожно провести коррекцию управления до того, как они повлия %авл°" "Рметр процесса. Этот подход, который называется упрежда* "°вь1сц""* возмущению (feedforward from process disturbances), может за) ть качество управления. Ниже его иллюстрируют несколько примеров.

ировка температуры в помещении

Измере управления температурой в зданиях включают в себя датчик д 0 рар наружной температуры. Когда наружная температура изменяет ссматривается как "возмущение"), управляющий сигнал на клапан р