Глава 6. CTpyiqpM Управп

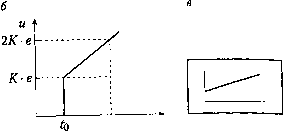Ti время

to время

Рис. 6.9. Переходная характеристика ПИ-регулятора: а - скачок ошибки происходит в момент q; б - выход интегральной части регулятора возрастает с течением времени до тех пор, пока ошибка постоянна; в - обозначение ПИ-регулятора на блок-схеме

Регулятор можно также описать с помощью преобразования Лапласа. Применяя его к уравнению (6.12), получим

U{s) ~ Щ{в) = bU{s) = Ufis) + Uj(s) + Ur)(s) = 1

К-

.£(5)

(6.13)

1 + Ti-s + Ti-T

E{s)

где E(s) задано уравнением (6.2), a Up(s), Uj(s) и [/(s) - изображения Лапласа Л1я компонент сигнала Up(t), Ujii) иир{() соответственно. Степень числителя превосходит степень знаменателя, поэтому усиление регулятора стремится к бесконечности при высоких частотах - это следствие дифференциальной составляющей. На практике дифференцирование нельзя выполнить точно, поэтому используется аппроксимация первого порядка с постоянной времени Tj и уравнение ПИД-регулятора принимает вид

6U(s)=Up(s) + Uiis)+Up,(s) = K]i+ "

Eis)

(6.14) оянно"

Часто постоянная времени фильтра нормализуется относительно пост времени дифференцирования

где N - число порядка 5-10. Усиление дифференциальной части регулятора [УР нение (6.14)] на высоких частотах при этом ограничено значением К- N.

ПИД-регулятор представляет собой частный случай обобщенного регуля [уравнение (6.7)] и может быть выражен через полиномы й, 5 и Г. Уравнение ( можно переписать в виде

s-ii + Ts)- 5C/(s) = К- [Т - s (\ + Tj-- s) + i + Tj- s + Т - Tj- s] Eis) Если это выражение разделить на Г,- • Гу, то в результате получим ПИД-ргУ-" в формате уравнения (6.7), для которого

.лятор;

злоговый ПИД-регулятор 1

Ris)

5(s) = r(s) = К

s+-

Ti-Tf

Как уже указывалось, регулятор, описываемый уравнением (6.7), может сдви-все полюса и тем самым изменить динамические свойства замкнутой системы. Боагодаря тому что ПИД-регулятор представляет собой систему второго порядка, его можно успешно применять для управления процессами с динамикой второго

порядка.

В действительности большинство технических процессов имеют порядок выше, чем второй, однако ПИД-регуляторы часто можно успешно использовать и для управления такими процессами. Это связано с тем, что многие процессы, имеющие в действительности динамику более высокого порядка, приближенно ведут себя подобно системам второго порядка. В системах, которые нельзя аппроксимировать уравнениями второго порядка, применение ПИД-регуляторов не рекомендуется. В частности, это относится к механическим системам, имеющим несколько колебательных составляющих движения {oscillation modi).

6.4.2. Дифференцирование измерительного сигнала

В некоторых системах управления процессами опорное значение время от времени резко изменяется, а между скачками остается постоянным. Скачок опорного значения обычно приводит к резкому изменению выходного сигнала регулятора; этот эффект иногда называют "всплеском производной" {deiivativekick). На рис. 6.10 приведена переходная характеристика ПИД-регулятора, которая часто используется как его символическое изображение в блок-схемах управления процессами.

tQ время

время

Дит Реходная характеристика ПИД-регулятора: а - скачок ошибки происхо-

чине 0 ~ дифференциальная часть регулятора - причина всплеска в вели-

выходного сигнала; в - обозначение ПИД-регулятора на блок-схеме

ijjug"! Предотвращения всплеска, дифференциальный член вычисляют на основе Вйидр" только выходной величины y(t). Производная ошибки записывается

de du dt dt dt

Если изменения опорного значения не учитываются дифференциальной Часщ регулятора, то в результате идеальный ПИД-регулятор принимает вид

Глава 6. Структуры yпpaвлe g 4 нагюгоьй ПИД-регулятор

6u(t) = К

e(t)+-\e(t)dx-T Ч О

dy dt

(6.16)

Для производной вновь применяется аппроксимация первого порвдка с постод)). ной времени Гу

bU{s) = K-

Eis) - К

\ + Tj-s

Y{s)

(6.17)

Этот метод исключения всплеска производной является стандартиым для большинства выпускаемых регуляторов.

6.4.3. ПИД-регулятор как каскад регуляторов

Поскольку передаточные функции ПИД-регулятора [уравнения (6.14) и (6.17)] состоят из суммы трех членов, их можно рассматривать как параллельное соединение пропорционального, интегрального и дифференциального регуляторов. Однако его можно представить как последовательное (каскадное) соединение ПИ-регулято-ра с пропорционально-дифференциальным (ПД, Proportional-Derivative - PD) регулятором. ПИ-регулятор [уравнение (6.14)] описывается выражением

5f/(s)

E(s)

Тг-s

a ПД-регулятор

E{s)

1 +

\ + {Tf+Ta)-s

В результате последовательная форма ПИД-регулятора имеет вид

Eis)

1 +

Преобразование из параллельного представления в последовательное возл лишь при условии

Tj«T«Ti

Усиление регулятора как функция частоты показано на рис. 6.11. При вЫ частотах усиление стремится к значению

10*н«

Из графика рис. 6.11 следует, что ПИД-регулятор можно рассматривать каК J, тание фильтров низкой и высокой частоты, включенных последователь <„i дел 5.3). Эта конфигурация называется опережающе-запаздывающим фИ {lead-lagfiher).

\Gpid

1 1 Jd Jf

Рис. 6.11. Логарифмическая частотная характеристика {Bode plot) ПИД-регулятора в последовательном представлении

6.4.4. ПИ-регулятор

Если фильтр низких частот соединить последовательно с ПИ-регулятором или если два ПИ-регулятора соединить каскадно, то получится структура, известная под названием ПИ -регулятор {PIPI controller). ПИ-регуляторы иногда используются в системах электропривода. Фильтр низких частот ослабляет уровень высокочастотных сигналов. В системах механического привода могут возникать резонансные колебания, которые хорошо гасятся таким фильтром. Передаточная функция ПИ-регулятора описывается выражением

GpipM) = К

l + r.-s 1 + Г.

Ti-s

i + Tn-s

где Т- - постоянная времени интегрирования, а Ц > > Г3. Значение обычно принимается равным резонансному периоду (т. е. величине, обратной резонансной частоте) управляемого физического процесса. Зависимость усиления от частоты по-«зана на рис. 6.12.

1 11

72 7з

Рис. 6 12 тт л,

• -Логарифмическая частотная характеристика ПИ-регулятора

0.45

Другие виды параметризации ПИД-регулятора

"Уравн? ПИД-регулятор параметризуется в соответствии со следу

6u(t) = Кр - e(t) + Ki \e{r)dr + •

(6.18)

Эта параметризация эквивалентна уравнению (6.12). Однако существует ва практическое ограничение, из-за которого уравнение (6.18) нельзя применять*"" версально. Усиление всего "классического" ПИД-регулятора [уравнение (6l2"

Глава6. Структурыуправд рр.пизация ПИД-регулятора

можно

изменять с помощью единственного параметра/С, что очень удобно, в частц

сти, при пуске или настройке технического процесса. Этот эффект очевиден и

изло.

гарифмической частотной характеристики, изображенной на рис. 6.11. У класси кого регулятора при изменении К вся характеристика смещается вертикально а* форма остается неизменной. Иными словами, усиление изменяется одинаково дл* всех частот. В параметрической форме (6.18) при любой модификации параметров изменяется не только усиление, но и точки излома отдельных отрезков логарифм ческой частотной характеристики.

У идеального регулятора три параметра - К, Tj и - можно настроить индивиду, ально, однако на практике, если регулятор изготавливается по аналоговой технолоти отдельные режимы управления обычно влияют друг на друга. Это влияние может оказаться настолько значительным, что действительные и номинальные значения параметров будут отличаться на 30 %. В цифровых системах управления параметры регулятора можно настроить с необходимой точностью, а их взаимное влияние отсутствует.

6.5. Реализация ПИД-регулятора

При реализации регулятора необходимо принять во внимание много различных факторов. Прежде всего следует разработать дискретную модель регулятора и определить соответствующую частоту выборки. Амплитуда выходной величины регулятора должна быть "реалистичной", т. е. находиться между минимальным и максимальным допустимыми значениями. Это ограничение вызывает дополнительные проблемы npi реализации и эксплуатации. Во многих приложениях должен быть ограничен не толь ко выходной сигнал, но и скорость его изменения из-за физических возможностей ис полнительных механизмов и предотвращения их чрезмерного износа. Изменение ни строек параметров и переключение с автоматического режима работы на ручной и другие изменения условий эксплуатации не должны приводить к возмущениям р0 лируемого процесса. Все эти проблемы рассмотрены в этом разделе.

Регуляторы можно создать по аналоговой технологии на базе операционных У лителей или, что становится все более распространенным, как цифровые устро" на основе микропроцессоров. При этом они имеют практически одинаковый шний вид - регулятор заключен в небольшой прочный корпус, который допу установку в промышленной среде. j.

Несмотря на то что цифровая технология имеет много преимуществ, анало подход по-прежнему сохраняет свои позиции, так как он является основой для ровых решений. К очевидным преимуществам цифровых регуляторов относите можность с помощью каналов связи соединять их друг с другом, что позволяе изводить обмен данными и применять удаленное управление. В этом Р приведен пример программы для цифрового ПИД-регулятора.

6.5.1. Дискретная модель ПИД-регулятора

Для того чтобы аналоговый регулятор реализовать программно, нео...--дискретная модель. Для этого применяются те же методы, которые описанЫ в Р

4 для низкочастотных и высокочастотных аналоговых фильтров и их преобразо-в цифровые.

рсли регулятор первоначально проектируется на базе аналогового описания, а застроится его дискретная модель, при достаточно малых интервалах выборки про-yg по времени заменяются конечными разностями, а интегрирование - сум-ованием (раздел 3.4). Этот подход будет использован и в данном случае, ошибка выходной величины процесса [уравнение (6.1)] вычисляется для каждой лки

e(kh) = uikh) - y(kh) (6.19)

Предполагается, что интервал выборки h является постоянным. Любые изменения сигнала, которые могли подойти в течение интервала выборки, не учитываются (разделы 5.1.3 и 5.1.4).

Существует два типа алгоритма регулятора - позиционный и приращений. Позиционный алгоритм

В позиционном алгоритме (position form) выходной сигнал представляет собой абсолютное значение управляющей переменной исполнительного механизма. Дискретный ПИД-регулятор имеет вид

u(kh) = Mq + Up(kh) + uj(kh) + ug(kh) (6.20)

Даже при нулевой ошибке управления выходной сигнал отличен от нуля и определяется смещением Mq.

В соответствии с уравнением (6.14) пропорциональная часть регулятора имеет вид

Up(kh) = Ke(kh) (6.21)

Чнтеграт аппроксимируется конечными разностями

"°стоя„„ой

4kh) = u,[(k - 1)А] + /С. А . ,kh) = uA(k -тК-а- e(kh) (6.22)

Be "

?пoэVoLTГжнTп ™r """" """ стать очень ма-

?омашин1™!„™°™"" ° ™м, чтобы обеспечить необходимую точ-

-Юсть

НфепГ"™™"Р"™я. "РаЖениГД™" -асть ПИД-

[еобходимую

«ия(б.15)

регулятора получается из (6.17) подстановкой

Т • s

Uo(s) = -K--- ¥(3)

(6.24)

ТР атствующие дифференциальные уравнения, связывающие u(t) uy(t), име-