Пример 3.9

Станция очистки сточных вод с замкнутым циклом - простая модель взаимодействия микроорганизмов с загрязнениями

Качественное описание работы станции биологической очистки сточных вод приведено в разделе 2.4.2. Входной поток сточных вод характеризуется концентрацией загрязнений и не содержит живых организмов. В аэраторе -в предположении, что компоненты равномерно перемешаны, смесь загрязнений с концентрацией s и микроорганизмов с концентрацией находится во взвешенном состоянии. Расходы показаны на рис. 3.11.

входной поток = Q

аэратор

Q+Qr

вьосод очищенной воды

устройство осаждения

ггтттттттт

входной поток воздуха

отстой

на переработку

рециркуляция микроорганизмов = Qr Рис. 3.11. Простая модель аэратора станции очистки сточных вод

Баланс массы загрязнений и микроорганизмов в аэраторе записывается в виде приращение массы = втекающая масса - истекающая масса -ь рост - распад

Микроорганизмы возвращаются из отстойника с концентрацией с.. Показатель роста микроорганизмов моделируется величиной р • с, при этом удельный показатель роста р зависит от концентрации загрязнений

р = Д.

где К - постоянный параметр. Рост практически отсутствует при малых значениях S и приближается к максимальному значению Д при высокой концентрации загрязнений. Концентрация микроорганизмов уменьшается из-за их гибели со скоростью, пропорциональной концентрации b с. Уравнение баланса массы микроорганизмов имеет вид

V--QrC„-{Q+Qr)-Cx+ -i-c-b-c,) at

Загрязнения попадают в аэратор из входного потока и при рециркуляции из отстойника. Поскольку предполагается, 4jo загрязнения растворены, их концентрация одинакова и в аэраторе, и отстойнике. Загрязнения перерабаты-

ваются в аэраторе из-за метаболизма микроорганизмов. Соответствующая п оизводительность переработки загрязнений определяется величиной f-x/Y, где переменная F называется коэффициентом воспроизводства {yield factor). Тогда уравнение баланса масс загрязнений можно записать в виде

V~(-s, + Q,-s-{Q+Q,)-s-V-c

Очевидно, что динамика системы является нелинейной - удельный показатель роста р зависит от концентрации загрязнений, а расход умножается на концентрацию.

3.2.4. Уравнения сохранения энергии

В некоторых процессах необходимо регулировать температуру. Динамическая модель системы управления температурой должна учитывать тепловые потоки и накопление тепловой энергии. Во многих случаях поток тепла через объект пропорционален разности температур на его границах

где q ~ поток тепла, R - тепловое сопротивление и Г - температура. Перенос тепла часто моделируется как величина, пропорциональная площади поверхности А и обратно пропорциональная длине пути / теплового потока

R I

rjxek - теплопроводность. Сохранение тепловой энергии можно описать как

~~ теп.доемкость, q - алгебраическая сумма входящих и исходящих тепловых потоков.

Пример 3.10

Тепловой баланс жидкости в баке

Тепловой баланс жидкости в баке служит иллюстрацией закона сохранения энергии (рис. 3.12). Температура жидкости Годнородна внутри бака, температура Окружающей среды - Г,,, а теплоемкость бака - С,. Суммарное тепловое сопротивление верхней и нижней частей - а боковых стенок - i?2- Нагревательный элемент подводит к жидкости тепловую энергию и.

Тепловой баланс

dT 1 1

с,.. = «,-(--)-(г-г„)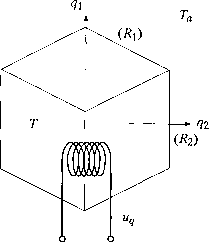

Рис. 3.12. Система в состоянии теплового равновесия (Г - температура окружающей среды, Т- температура в баке)

Больщая разница температур на внутренних и внещних поверхностях стенок будет вызывать быстрые температурные изменения в баке. Чем больше R- и i?2> тем медленнее будут изменения.

3.3. Непрерывные модели динамических систем

3.3.1. Описание систем во временной и частотной областях - исторический обзор

Описание динамических систем обыкновенными дифференциальными уравнениями восходит, по крайней мере, к Исааку Ньютону. Вероятно, первым провел систематическое изучение устойчивости систем с обратной связью Джеймс С. Максвел.л на примере центрифужного маятникового регулятора, разработанного примерно» 1788 году Джемсом Уаттом для управления его паровой машиной. В своей статье 1868 года Максвелл вывел дифференциальные уравнения регулятора, линеаризова их в окрестности точки равновесия и показал, что устойчивость системы зависит оТ корней ее характеристического уравнения. Если эти корни имеют отрицательные ве щественные части, то система устойчива.

Важнейшая технологическая задача для США в 1910-1920 годы - создание ме* континентальной телефонной связи. Соответствующие исследования привели

К"

Создание Харальдом С. Блэком (Harald S. Black) усилителя с обратной связью ило эту проблему. Внедрение новых и более сложных технических систем требо-ало в то же время использования новых математических методов. Для систем из пятидесяти и более усилителей анализ характеристического уравнения больше не подходил Поэтому инженеры в области связи и электронных устройств разработали новый метод исследований на базе комплексного анализа и предложили концепцию частотных характеристик. В 1932 году американец шведского происхождения Гарри Найквист (Наггу Nyqvist) опубликовал свою знаменитую теорему о том, как определить устойчивость по форме частотной характеристики. Критерий Найквиста, который в момент своего появления считался революционным, на сегодняшний день представляет собой лишь небольшую часть вводных курсов по теории управления. Но в те времена военные считали эти теорему настолько важной, что США держали ее в тайне до конца Второй мировой войны.

В большинстве случаев технические процессы очень сложны и нелинейны. В 1940-е годы стал стандартным подходом метод обратной связи; были разработаны устройства на базе концепции пропорционально-интегрально-дифференциального (ПИД) регулирования (раздел 6.4). Метод частотных характеристик доказал свою эффективность для анализа линеаризованных моделей динамики процессов.

В 1950-е годы некоторые исследователи вернулись к описанию систем обыкновенными дифференциальными уравнениями как основе управления процессами. Это направление было стимулировано американской и советской космическими программами, поскольку обыкновенные дифференциальные уравнения представляют собой естественную форму описания динамики космических кораблей. Тенденция усилилась с появлением цифровых ЭВМ, которые позволили проводить расчеты, ранее практически не применявшиеся из-за огромных затрат времени. Цифровые ЭВМ требовали, в свою очередь, новой математики. Инженеры работали с дифференциальными уравнениями состояния, а не впрямую с частотными или характеристическими уравнениями. Были введены новые фундаментальные понятия - управляемость, наблюдаемость и обратная связь по переменным состояния. Для решения задачи оптимизации траектории полета были разработаны новые разделы вариационного исчисления.

В химии и механике естественным является вывод дифференциальных уравнении Модели на базе физических свойств системы. Такой подход возможен и в других приложениях, но, несмотря на это, ПИД-регуляторы используются во многих техни-

ких решениях. Поэтому обычной практикой является применение и дифференци- ьных уравнений, и частотных характеристик. Описания в частотной области по-Режнему популярны в электротехнике и электронике и совершенно естественны Обь приложений. Сложные системы предпочтительнее описывать в терминах

кновенных дифференциальных уравнений.

многим важным открытиям в электронике и теории управления и заложили фунД 3.3.2. Упявнрнма мент их становления как научных дисциплин. Благодаря разработке после Перво! ми

состояния

мировой войны электронного усилителя стали возможны междугородные телефонные звонки. Д.11Я компенсации потерь электроэнергии на больших расстояниях необходимо было использовать много усилителей, последовательное включение ко рых однако приводило к большим искажениям, поскольку нелинейности каждог» усилителя также усиливались последующим каскадом устройств.

Дифференциальные уравнения, описывающие физический процесс, всегда bqj,"° "Робразовать к системе обыкновенных дифференциальных уравнений пер-или том случае говорят, что это описание в виде уравнений состояния

в пространстве состояний {state-space form). Главное преимущество такой РМы записи в том, что для решения этих уравнений можно использовать числен-

ные методы. Кроме того, четко прослеживается физическая сущность процесс в частности связь между внутренними переменными и внещними входным и вы ходным сигналами. Аналогично, изучение систем управления с более чем одни входом и выходом, проще в форме уравнений состояния. Основой математическогг аппарата для моделей в пространстве состояний служит, главным образом, лине пая алгебра - векторная и матричная нотации значительно упрощают описание Однако методы линейной алгебры не требуются, чтобы получить основные пред, ставления о динамике системы.

Большинство физических процессов можно моделировать на основе функцио-нальных блоков, аналогичных описанным в примерах раздела 3.2. В общем случае уравнения баланса нелинейны и, как правило, связаны друг с другом. Таким образом описание динамики процесса может представлять собой набор нелинейных, связан ных между собой дифференциальных уравнений первого порядка для баланса энер гии, общей массы, массы компонентов, сил и моментов.

Уравнения состояния представляют собой практичный и удобный способ описания динамических систем. Состоянием называется набор всех переменных - так на-зываемых переменных состояния {siate variables), производные первого порядка и которых входят в уравнения описания динамической системы. Концепция уравне НИИ состояния имеет фундаментальное значение. Если известны текущее состояние системы (переменные состояния) и входные сигналы, то можно предсказать ее даль нейшее поведение. При этом предысторию, т.е. как было достигнуто текущее состоя ние, знать не нужно. Другими словами, состояние - это минимальное количество информации о системе, которое необходимо, чтобы предсказать ее будущее поведение,

Состояние X можно представить как вектор-столбец, компоненты которого - переменные состояния

x = (xi Х2 ... х„)

Непосредственно измерить все переменные состояния можно в редких случаях-т. е. существуют внутренние переменные, за которыми не удается следить с помощь» датчиков. Поэтому описание в пространстве состояний называют также внутренним описанием (internal description). Выходные величины - измерения, обозначаются через z/j, г/2,Ур и составляют вектор у

У = (г/1 У2 - ypf

В общем случае число датчиков р, связанных с техническим процессом, меныи числа переменных состояния п. Поэтому вычисление х по у - нетривиальная задача-

На любую техническую систему влияют входные сигналы двух типов - сигналЫ-которые можно изменять вручную или автоматически какими-либо техническим средствами, и сигналы, которыми управлять невозможно. Сигналы первого типа называются управляющими сигналами или переменными управления mj, U2, -, ишсо ставляют вектор и

u = (Ml U2 ... м,-)

Входные сигналы второго типа могут влиять на систему, но не поддаются упра» лению. Величина этих сигналов отражает влияние внешней среды на систему, напри .мер изменение (возмущение) нагрузки, вызванное температурой, радиацией, неЖ

ельным магнитным воздействием ("наводками") и т. п. Все эти сигналы обознача-йТся вектором V

V = (»! V2 ... vj

Целью системы управления является вычисление на основе имеющихся измерений у таких управляющих сигналов и, чтобы, несмотря на влияние возмущений v, техническая система выполняла поставленные задачи. Управляемую систему можно педставить в виде блок-схемы (рис. 3.13), на которой показаны управляющие сигналы, возмущения и выходные переменные.

Рис. 3.13. Блок-схема управляемой системы

Эта концепция объясняется на следующем простом примере.

Примерз.11

Механическая система

Система в примере 3.2 (раздел 3.2.1) имеет две переменные состояния - положение z и скорость V. Входная переменная и - это сила/. Положениеz (выходная переменная) можно измерить. В векторной форме система описывается как

x = (z w)T; u = F; y = z = (l 0)-х

Уравнения состояния имеют вид

I о

и; у = (1 0)-х

• Описание линейной системы в пространстве состояний

ие си ™"тво примеров из раздела 3.2 представляют собой линейные дииамичес-Уравне """""У можно смоделировать линейными дифференциальными сос-год в которых отсутствуют члены, содержащие произведения переменных

Тема одных и выходных сигналов - типа х, х и или • Х2. Линейная сис-

. имеющая п переменных состояния и г входных переменных, описывается сле-тЦими уравнениями состояния с постоянными коэффициентами;