3.1.4. Моделирование дискретных событий

Моделирование систем, основанных на последовательности дискретных собц. тий, принципиально отличается от моделирования динамических систем с помощц) математических соотношений. Для управления на основе обратной связи температу. рой, уровнем жидкости или давлением модель процесса фактически не нужна В этом случае значение контролируемого параметра поддерживается на заданнощ уровне с определенной точностью с помощью включения и выключения исполни-тельного механизма.

Связной теории для моделирования управления последовательностью пока нет. При бинарном управлении уже на стадии анализа системы должны быть рассмотрены все возможные нештатные и аварийные ситуации. Что будет, если сломается насос либо датчики или отключится питание и т. д.? Подготовка исчерпывающего списка всех возможных событий в системе - сложная задача, которую нельзя решить на основе систематической теории.

Для участка, описываемого в разделе 3.7, на котором станки обслуживаются роботом, необходима модель синхронизации. Эта задача принципиально отличается от простого управления на основе обратной связи. Синхронизация должна быть корректной в том смысле, что определенные детали должны быть доставлены конкретному станку в соответствующее время и в соответствующем порядке. Эта задача имеет много общего с операционной системой, которая управляет ресурсами ЭВМ; в определенных случаях для решения таких задач можно использовать теорию очередей.

3.2. Основы моделирования динамических систем

Физический подход к моделированию динамических систем основан на уравнения.: баланса сил, массы, энергии и моментов. В этом разделе на простых примерах рассмотрены некоторые общие принципы моделирования динамических систем.

3.2.1. Механические системы

Краеугольным камнем динамической модели любой механической системы яв.чя-ется второй закон Ньютона.

Для применения закона Ньютона необходимо задать некоторую систему отсчета относительно которой будут определяться положение, скорость и ускорение. Пуст вектор F - сумма всех сил, действующих на тело, т - масса тела, а вектор z характе ризует его положение. Ускорение а - вектор с тем же направлением, что и вектор Уравнение ба.панса сил имеет вид

F = от а = и - -гт" dt

В действительности Ньютон сформулировал свое утверждение относительно иМ пульса да • v следующим образом

F= -r{m-) at

Второй закон Ньютона можно записать как систему дифференциальных уравне-ий первого порядка, в форме так называемых уравнений состояния (раздел 3.3.2). При прямолинейном движении координата z и скорость v выражаются как скаляры

dv F

dt m

Более общая форма уравнений динамики - это уравнения Лагранжа. Пример 3.2

механическая система с пружиной и амортизатором

Многие механические системы аналогичны показанной на рис. 3.1. Тело массы т связано с неподвижной стеной пружиной и амортизатором. Сила реакции пружины пропорциональна ее относительному растяжению, а сопротивление амортизатора - скорости тела.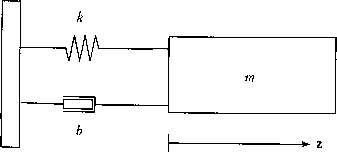

Рис. 3.1. Закон Ньютона для прямолинейного движения

Закон Ньютона в этом случае записывается в виде

d4 , dz m-~b---dt -k-z + F dt dt

После простых преобразований получим

dz dzk F -- dt?- m dt m щ.

"Изм 7" примера 3.2 можно использовать для описания многих сервомеха-Фиц ственно решение уравнения зависит от относительной величины коэф-Циентов Ь, кит. При малом коэффициенте демпфирования b уравнение описыва-"олебательный процесс, а при больших значениях b колебания отсутствуют.

Системы такого рода часто характеризуются относительным демпфированием, час, тотой собственных колебаний, шириной полосы пропускания и коэффициентом уси, ления.

Закон Ньютона для систем вращения имеет вид

где т - сумма всех моментов, действующих на тело, J - момент инерции и (о - уго. вая скорость (рис. 3.2). Часто J - непостоянная величина, например, при работе про мышленного робота или прокатного стана, и нужно учитывать его зависимость oi времени.

Глава 3. Описание и моделирование систе,, о о основы моделирования динамических систем

--.----- -------

т,(о

Рис. 3.2. Закон Ньютона для вращения

Если ввести понятие угла поворота £, то динамику вращения можно описать в фор ме уравнений состояния. При этом полагают, что известно направление вращения» что величина J постоянна. Тогда дифференциальные уравнения записываются в виде

- = ш dt.

dw Т 7

Пример 3.3

момент электрического двигателя

Электрический двигатель связан с нагрузкой жестким валом. Результирующий момент Г - разность между вращающим моментом и моментом сопротивления нагрузки Т. Момент двигателя Г,„ является функцией тока ротора, магнитного потока и, в некоторых типах двигателей, угловой скорости и угла поворота. Ток зависит от переходного процесса в цепи ротора.

Момент сопротивления нагрузки также зависит от многих факторов. Кулоновское трение вызывает момент cIq, который зависит не от скорости, а только от направления вращения и действует всегда против него (рис. 3.3). В некоторых системах есть вязкое сопротивление с моментом ш. характеризующееся параметром d. В компрессоре или насосе момент сопротивления

нагрузки также зависит от турбулентности жидкости и пропорционален квадрату скорости - <2 ю, где параметр зависит от условий работы.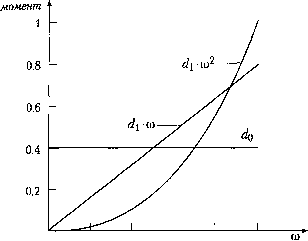

О 0.2 0.4 0.6 0.8 1

Рис. 3.3. Момент двигателя как функция угловой скорости

В итоге полный момент сопротивления нагрузки можно представить суммой упомянутых моментов и момента внешней нагрузки Tq.

= dQ- sign(a)) + d ш + d2- 4)- + Tq

Функция sign(ro) принимает значение -i-l для положительного аргумента ю и -1 - для отрицательного и используется для обозначения направления. Общий баланс моментов ротора

</со)

£Де / - полный момент инерции двигателя и нагрузки.

Промышленный робот - это сложная механическая система, состоящая из связанных жестких рычагов. Описание динамики движения манипулятора робота базируется на законах Ньютона. Уравнения Лагранжа являются обобщенной формой закона Ньютойа. Существуют деформируемые механические системы, например крыло самолета, при движении которых могут появляться нежелательные колебания; такие динамические системы, вообще говоря, очень сложны для управления.

"•2. Электромагнитные цепи

Динамика большинства электромагнитных цепей определяется несколькими основными законами Законы Кирхгоффа описывают связь между напряжениями и Токами в электргшеской цепи. Электрические цепи образуются ветвями и узлами, етвь {branch) определяется как проводник или элемент с двумя концами. Элемент

Глава 3. Описание и моделирование систе» ,сновы моделирсншшуццийИеских систем

ветви может быть пассивным, т. е. сохраняющим или потребляющим ток, или актив, ным, т. е. генерирующим напряжение и.пи ток. Узел {node) - это точка, в которое соединяются три или более ветвей. В узле ток может иметь более чем один путь. Закон Кирхгоффа для тока утверждает, что

сумма всех токов в любом узле равна нулю

а закон Кирхгоффа для напряжений -

сумма падений напряжения по любому замкнутому контуру равна нулю

Закон Кирхгоффа для напряжений есть спедствие принципа сохранения энергии. При записи баланса напряжений можно идти вокруг замкнутого контура в любом направлении и суммировать падения напряжения при условии, что каждый элемент учитывается только один раз.

Основы электромагнитной теории сформулированы в уравнениях Максвелла, С точки зрения динамических систем имеется два элемента с зависимым от времени состоянием: конденсатор - для накопления электрического заряда и индуктивность - для накопления энергии магнитного поля.

Конденсатор в цепи накапливает э.яектрический заряд, т. е. энергия сохраняется в электрическом поле. Ток, текущий через конденсатор, пропорционален производной от напряжения на конденсаторе по времени

где С - емкость конденсатора.

Пример 3.4

Простая резистивно-емкостная цепь

Рассмотрим простую резистивно-емкостную {RC) цепь (рис, 3.4) и проанализируем зависимость напряжения на конденсаторе от напряжения источника.

Рис. 3.4. Пассивный низкочастотный ЛС-фильтр первого порядка Закон Кирхгоффа для напряжений цепи дает

где R - активное сопротивление, а »„ - напряжение на конденсаторе, опреде-;ое уравнением

dv„ 1

После исключения тока г из дифференциального уравнения, имеем

R-С-

= - о„ + о,

Это дифференциальное уравнение первого порядка характеризуется .\я*н стоянной времени {time constant)

T=R-C

Если начальное напряжение на конденсаторе равно нулю, то скачок входного напряжения в,- вызовет экспоненциальный рост напряжения на конденсаторе

v,{t) = v{i-e/)

На рис. 3.5 показаны переходные процессы {traiisient response) в ЛС-цепи для различных значений постоянной времени - с ростом Греакция процесса замедляется.

тпряжение 1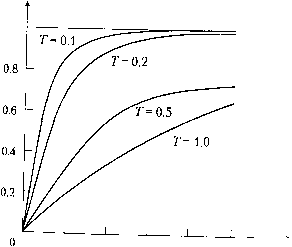

0.6 0.8 1

Рис. 3.5. Изменение напряжения на конденсаторе в йС-цепи при скачке входного напряжения для раз.шчных значений постоянной времени R С

В электронике и технике связи обычной практикой ся использование синусоидального входного сигнала. I Ное напряжение цепи имеет вид

рДО= Vi-sm{(at)

где - максимальное значение амплитуды. Выходное напряжение на конденсаторе через некоторое время также станет синусоидальным.

анализа систем являет-сигнала. Предположим, что вход-