Выходной сигнал имеет такую же частоту, что и входной, но другие амплитуду и фазу:

Оо(0 = У о sin(co/ - ф)

где = l/;/Vl + (co-y?- С)2иф = arctg(cD R-С).

С ростом частоты амплитуда выходного напряжения падает и все больше и больше отстает по фазе. Цепь с такими свойствами называется низкочастотным фильтром (low-pass filter), поскольку она пропускает низкие, но гасит высокие частоты.

Приведенный пример иллюстрирует два основных метода описания линейных систем - во временной области (time-domain) и в частотной области (frequency-domain). Анализ во временной области рассматривает поведение системы во времени, т. е. зависимость от времени ее реакции на конкретный входной сигнал - скачок. Частотный анализ исследует поведение системы под воздействием внешних возмущений различной частоты.

При изменении магнитного поля во времени возникает электрическое поле. Это - закон Фарадея (закон электромагнитной индукции), который описывается одним из уравнений М аксвелла. В соответствии с законом индукции напряжение е -э.д.с. индукции, - наведенное на концах идеальной катушки, т. е. катушки без активного сопротивления, равно

где - потокосцепление витков катушки (потокосцепление - это произведение магнитного потока Ф через один виток на число витков N). Потокосцепление катушки с током / и индуктивностью L

Другими словами, в катушке (индуктивности) энергия сохраняется в магнитном поле.

Дифференциальньге уравнения для емкости и индуктивности представляют собой основу для описания электромагнитных цепей. Другие отношения можно получить из этих основных уравнений с помощью алгебраических преобразований. Соотношение между магнитной индукцией В и напряженностью магнитного поля определяется свойствами среды

В = р-Я

где ц - магнитная проницаемость материала.

В ферромагнитных материатах проницаемость непостоянна и для больших значений Я величина магнитного потока Ф, пропорциональная магнитной индукции В-будет достигать насыщения. Связь между магнитным потоком и током, создающие напряженность магнитного поля, показана на рис. 3.6.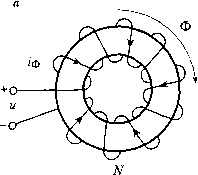

линейная зона

отрицательное насыщение

положительное насыщение

Рис. 3.6. Простая магнитная цепь (а); типовая кривая намагничивания без гистерезиса (6)

Часто при описании магнитных цепей необходимо учитывать явление гистерезиса, из-за которого магнитная индукция не только функция тока, но и зависит от предыстории намагничивания.

Пример 3.5

Двигатель постоянного тока с независимым возбуждение

Двигатель постоянного тока (d.c. motor) преобразует электрическую энергию в механическую в виде вращающего момента (рис. 3.7).

питание цепи возбуждения статора -О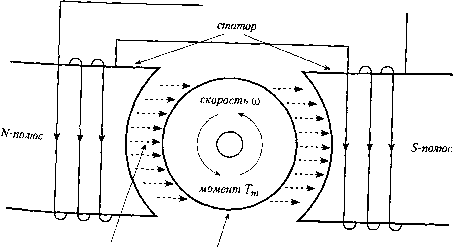

ротор

i двигателя постоянного тока

магнитный поток •""•З.?. Схема.

"ос?оянныГ существуют два магнитных поля. Поле статора создается или янным магнитом, или электромагнитом; последний должен быть соели-

нен с отдельным источником напряжения. Для простоты будем здесь полагать, что поле статора постоянно во времени. Магнитное поле ротора возникает при подаче напряжения в цепь ротора.

Обмотки размещаются таким образом, что поле ротора всегда перпендикулярно полю статора. Известно, что если два магнитных поля расположены под углом друг относительно друга, то возникает момент, который стремится сделать их параллельными. Это принцип работы стрелки компаса - если стрелка не параллельна линиям магнитного поля Земли, то она поворачивается, пока не установится параллельно. Ротор под воздействием возникшего момента поворачивается, и его обмотки механически переключаются коммутатором, что приводит к изменению направления поля ротора. Таким образом, в результате ориентация поля ротора в пространстве всегда одинакова и перпендикулярна по отношению к полю статора. Момент же сохраняется постоянным для всех углов поворота ротора.

Момент, генерируемый двигателем, пропорционален магнитной индукции поля статора и току ротора i. Поскольку в этом примере мы предполагаем, что магнитная индукция постоянна, то момент двигателя

где - константа, зависящая от двигателя. Учитывая момент сопротивления нагрузки Tj, механическую часть можно записать следующим образом

Глава 3. Описание и моделирование систе QQHoBbi моделирования динамических систем

3 2-.---

(см. раздел 3.2.1)

(/со)

= k„-i-Tr

где J - полный момент инерции двигателя и нагрузки. В результате вращения в магнитном поле статора в обмотках ротора наводится э.д.с. индукции е. При постоянном поле статора э.д.с. индукции пропорциональна скорости вращения со

где k - константа. Если единицы согласованы и потери пренебрежимо

малы, то

kg=k„ = k

В соответствии с законом Ленца магнитный поток, вызванный э.д.с. индукции е, будет ориентирован против потока, вызванного исходным током проводника.

Электрическая цепь ротора характеризуется ее активным сопротивлением R и индуктивностью L. Предполагая, что L - константа, закон индукции определяет напряжения вдоль контура как

d4> d(L i)

L- - = V - R-i - k -dt

dt dt

где i - ток ротора, a » - приложенное напряжение. Динамика двигателя иллюстрируется рис. 3.8.

Приложенное напряжение вызывает ток ротора, создавая момент двигателя. Момент воздействует на ротор, который начинает вращаться с опреде-

ной угловой скоростью. Наведенная э.д.с. индукции действует как обратная связь между механикой ротора и его электрической цепью.

( механическая нагрузка

напряжение ротора

момент нагрузки

ток ротора

э.д.с. индукции

угловая скорость со

►0

момент двигателя

угловая скорость О)

электрическая цепь ротора механическая часть

Рис. 3.8. Блок-схема двигателя постоянного тока

3.2.3. Баланс массы

Для многих промышленных процессов существенным является моделирование оаланса массы различных компонентов. В открытой системе, где происходит обмен с внешним миром, все уравнения баланса массы имеют одинаковую структуру

приращение массы = приход массы - расход массы

Такое уравнение можно сформулировать как для каждого отдельного компонента, так и для всей массы в целом. Приход (расход) массы может быть следствием как родного (выходного) потока, так и химических реакций или биологического роста, есколько примеров иллюстрируют принципы уравнения баланса.

Пример 3.6

Баланс общей массы

Бак заполняется однородной несжимаемой жидкостью (рис. 3.9). Приход и расход массы обозначаются как q и (jyf соответственно. Уравнение баланса имеет вид

iout

полная масса.

Einaea 3. Описание и моделирош#щсист основы моделирования динамических систем

4out

Рис. 3.9. Емкость с однородной жидкостью

Пример 3.7

Баланс массы компонента

Бак наполнен раствором с однородной концентрацией одного, из компонентов с (рис. 3.10).

Поскольку объем У постоянный

V dc

- - = -С + С:

q dt

Вид этого дифференциального уравнения такой же, как и для электрической цепи в примере 3.4. Постоянная времени определяется здесь как Г= Y/q. Изменение концентрации в баке при скачке с, аналогично зависимости, пред-ставленой на рис. 3.5. Решение дифференциального уравнения имеет вид

с(0 = с,-(1-е-/)

Интуитивно ясно, что концентрация будет меняться медленнее, если расход жидкости во входном потоке мал по сравнению с объемом 1/(это соответствует большому значению Т). То есть баланс массы компоненты имеет такие же динамические свойства, что и низкочастотный фильтр.

В принципе, анализ рассмотренной системы можно выполнить и в частотной области, аналогично электрическому низкочастотному фильтру. В этом случае концентрация входного потока изменяется (модулируется) по синусоидальному закону и изучается частотный отклик концентрации в выходном потоке. Этот подход, однако, не очень практичен для химических процессов, так как постоянная времени может быть порядка часов и такой эксперимент продлится много дней.

Примерз.8

Рис. 3.10. Динамика концентрации в простом смесителе

Сформу.тируем баланс массы компонента. Концентрация раствора во входном потоке с, может меняться заданным образом. Расходы входного и выходного потоков считаются постоянными и равны q. Полная масса компонента в баке определяется объемом I/и равна V- с. Будем считать концентрацию в выходном потоке такой же, как в баке. Тогда баланс массы компонента записывается в виде

d(V-c)

Аэрация бака очистки сточных вод

Уравнение, описывающее концентрацию растворенного кислорода в аэраторе станции очистки сточных вод или в ферментаторе, является нелинейным. При этом полагают, что аэратор работает как дозатор, т. е. жидкость поступает в бак и вытекает из него не постоянно, а только в определенные моменты времени. Воздух подается от компрессора с расходом и.

Скорость перехода кислорода из газообразного состояния в растворенное определяется коэффициентом растворимости kj а. Для простоты будем полагать, что этот коэффициент пропорционален расходу воздуха:

k[ - а = а - и

где а - коэффициент пропорциональности. В свою очередь, коэффициент растворимости равен нулю при насыщенной концентрации раатворепного кис-орода (с = с) и максимален при нулевой концентрации; эта зависимость моделируется выражением а г/ • (с - с). Микроорганизмы потребляют растворенный кислород в процессе своего роста со скоростью R. Упрощенное уравнение баланса массы растворенного кислорода при концентрации с можно записать в виде

-=аи dt

(c-c)-R

Из-за наличия произведения и с система нелинейна.