вать регулятор. Соответственно, требуется меньшее число правил, поскодь оценивать меньше параметров, и во многих случаях регулятор на базе нечетко ки может вырабатывать решения быстрее, чем экспертная система на основе п "если-то". На экспериментальных прототипах было показано, что нечеткая п является хорошим инструментом при недостаточных объемах информации

Автоматический регулятор скорости поезда служит простой иллюстрацией ложений нечеткой логики. Критерием для регулятора является оптимизация в ни пути при известных ограничениях. Входными данными являются текущщ . рость, ускорение и расстояние до места назначения, на основе которых регудя управляет мощностью двигателя.

слишком\/ / \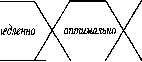

быстро

текущее состояние:

слишком медленно = 0.2, медленно - 0.8

трость

торможение

постоянная скорость

ускорение

текущее состояние:

снижение скорости =1.0

ускорение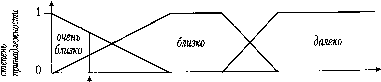

текущее состояние:

очень близко - 0.65, близко - 0.35

расстояние от жста назначения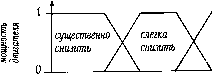

сохранять \/ аегка \/существенно постоянной/\ уваинить Аувешчитъ

выход регулятора

Рис. 3.21. Функции принадлежности регулятора скорости на основе нечеткой

ЛОГИК"

Функция принадлежности присваивает измеряемым величинам лингв кие значения (рис. 3.21). В приведенном случае ускорение имеет значение fj ние" из-за крутого подъема. Скорость принадлежит к множеству "медленно и "слишком медленно" (вес 0.2), а расстояние имеет значение "очень близко назначения" с весом 0.65 и "близко" с весом 0.35.

гике управления: медленно", а ускорение - "торможе-следует "существенно увеличить" мощность; о ость имеет значение "медленно", а ускорение - "торможение", то еле- Гетдаа увеличить" мощность;

расстояние имеет значение "близко", то следует "слегка снизить" мощность.

вило должно быть выбрано? Выход также имеет степень доверия, кото-т от степени доверия (т. е. веса) входных данных. Окончательный выбор рая pjgggMOM примере - "слегка увеличить" мощность. Даже если скорость значение "слишком медленно", то поезд уже близок к месту назначения.

Нет гарантии, что нечеткая логика может успешно справляться со сложными сис-тема.ми Регулятор на базе нечеткой логики является практически оценкой состояния системы, которая не основана на конкретной модели. Доказать устойчивость такого регулятора очень сложно.

Нечеткая логика приобрела чрезвычайную популярность при разработке систем управления в Японии, хотя в Соединенных Штатах, где была создана, и в других западных странах к ней относятся довольно сдержанно. Продукция, основанная на нечеткой логике, - вся она японского производства - включает в себя автоматически фокусирующиеся фотоаппараты, кондиционеры воздуха, стиральные машины, пылесосы, регуляторы лифтов и скорости поездов метро.

Аналогично другим техническим решениям, применение нечеткой логики должно рассматриваться с точки зрения эффективности, т. е. достижения приемлемых результатов при разумных затратах. Нельзя рассматривать нечеткую логику как всегда ьерное решение или как простую альтернативу более сложным схемам управления. В некоторых случаях, как для вышеупомянутых автоматически фокусирующихся фотоаппаратов, разработка более совершенной технологии датчиков фактически привела к лучшим результатам, чем использование нечеткой логики.

3-7. Комбинационные и последовательностные сети

ко прост™ "Р°™-нные процессы управляются бинарными сигналами; несколь-в разделеТ2"г"° управления последовательностью событий было приведено «.мбинаци " основе бинарных сигналов можно разделить на два типа - -ских вью """5* которые также можно рассматривать как совокупность логи-

Вкомбвд""" "°=ДОательностные сети, "ачением ""с""""" (combinationalnetwork) входная величина у с логическим овлетворят"" "ложь" зависит от ряда входных условий и, которые должны ься одновременно. У системы нет памяти, т. е.

тип-

y(t)-f[u(t)]

(3.22)

°сти ручного""" можно использовать, например, для проверки допус--"Щий компыо ™- Во время запуска сложного процесса вручную управ- %Дет включе Должен проверить выполнение всех логических условий прежде, "ледова" "" выключен конкретный исполнительный механизм. "0 Состояц""°""ой (sequencing network) выход зависит не только от те-я процесса и входных сигналов, но и от их истории. Такая система

"""ько правил могут дать представление о до Нескол имеет значение "слишком медл( если скор ----

имеет память и использует концепцию состояния объекта. В простой последоватед постной сети действия выполняются так

Шаг 1 => Шаг 2

Шаги

Когда переход от одного шага к другому определяется логическими ycлoвия, последовательность называют асинхронной. В отличие от этого в синхронных поц довательностях переход между состояниями (шагами) задается метками временц В промышленных приложениях чаще встречаются асинхронные переходы.

Некоторые идеи можно проиллюстрировать на упрощенном примере коордица. ции работы станков при поточном производстве. Два станка Ml и М2 образуют технологическую линию (рис. 3.22). буфере? между ними может содержать не более од. ной детали.

станок М2

Рис. 3.22. Два станка с промежуточным буфером на транспортере между ними

Каждый станок может быть в одном из двух дискретных состояний - "готов к ] те" или "неисправен". В течение короткого интервала времени At для каждого из двух станков существует вероятность, что он будет неисправен, - /j • Af и /2 • At. Вероят ность, что сломанный станок будет починен и снова запущен в работу в течение того же самого интервала времени, - rj • и Г2 • At. Буфер имеет два дискретных состояния-"полный" или "пустой". Пустой буфер будет полным, если станок Ml производит детали с вероятностью pj • At. Полный буфер может стать пустым, только если станок обработает накопившиеся детали с вероятностью Р2 Д- Поскольку состояния являются дискретными, их можно идентифицировать двоичными цифрами

О - станок неисправен 1 - станок готов к работе

О - буфер пустой 1 - буфер полный

Система описывается восемью состояниями (табл. 3.1).

Таблица 3.1. Описание дискретных состояний технологической линии

Станок Ml может выполнять работу, только если буфер пустой; is противном сЛ1 чае он должен ждать. Станок М2 может продолжать работу, только если буфер содеР

али- иначе он тоже должен ждать. Таким образом, работа каждого станка за-

состояния другого. Говорят, что станок "блокирован", если он не может ра-

" 3 за нехватки некоторых ресурсов (в данном примере деталей или свободно-ботатьиз

места в буфере).

° Работу станков иллюстрирует граф состояний (state graph) или конечный авто-т (automaton), описываемый восемью состояниями 5000,5111 (рис. 3.23). каждый момент времени система может находиться только в одном состоянии. Переход между состояниями определяется вероятностью, что станок выполнит свою боту за определенное время, или что он сломается, или что будет отремонтирован. Допустим, например, что система находится в состоянии 5101; при этом Ml простаивает а М2 может работать, поскольку буфер полный. Система может изменить это состояние тремя способами:

- если М2 сломан - переход в состояние 5100;

- если Ml отремонтирован - переход в состояние 5111;

- если М2 работает нормально - переход в состояние 5001.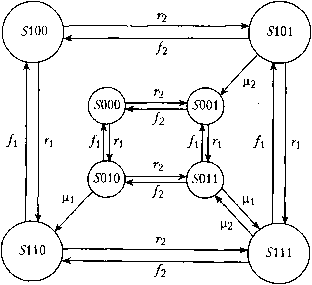

Рис. 3.23. Граф состояний технологической линии с двумя станками и буфером

6 РадТ° моделирования системы станков позволяет имитировать переходы

Чост!""" состояния. Фактически с помощью этой модели можно оценить вероят-Рость "" определенного состояния. Производительность станков и ско-альна "" влияют на общую эффективность работы системы в целом. Опти-CTa.rie" система не допускает простоя станков из-за блокировки или недостатка

р " " меет небольшую интенсивность отказов (failure rate). "Рило- представляет собой инструмент для систематического анализа

"Po\f,*" подобного рода и поэтому широко используется при проектировании

bnnjTfwtjt .r,r ------------- ч.

тленных приложений.

Процессы, в которых переход в другое состояние зависит только от текуц состояния и входных сигналов, называются марковскими процессами (aq process). В известном смысле марковские процессы похожи на дифференциаль! уравнения из раздела 3.4, однако между ними есть фундаментальное отличие в первом случае каждая переменная состояния имеет непрерывно изменяющуЦ, амплитуду (например, значение температуры или давления), но выборка и обрабц, ка происходят только в определенные моменты времени; напротив, марковский цесс "переключается" между конечным числом детерминированных состояний.

Граф состояний можно рассматривать как информационную структуру проц.. автоматизации. Она, однако, ничего не говорит о том, как реализовать управление В главе 7.будет показано, как использовать переключатели и программируемые л» гические контроллеры для создания таких систем.

3.8. Заключение

Модель есть описание физического процесса в целях управления. В этой глав( были рассмотрены четыре класса математических моделей:

- непрерывные динамические системы, описываемые линейными или нелиней ными дифференциальными уравнениями;

- дискретные модели динамических систем, описываемые линейными или нели-нейными разностными уравнениями;

- системы дискретных событий или последовательностные системы, описыва( мые конечными наборами состояний;

- системы с неопределенностями, которые описываются статистическими и.я лингвистическими методами.

Для компьютерного управления модель динамической системы должна быт: представлена в дискретном виде, либо в пространстве состояний (внутреннее npeJ ставление), либо как отношения вход/выход (внешнее представление) - выбор з< висит от структуры проектируемой системы управления. Линейные модели про» для анализа системы, но нелинейность не накладывает ограничений на компьютер ное управление. В этой главе были приведены примеры и нелинейных систем. Д исследования динамики линейных систем имеется целый ряд программных проДУ-тов, однако описание нелинейных систем очень сложно и редко может быть выпол* но аналитически. Поэтому важным инструментом моделирования таких систем я ляются программы-имитаторы.

В этой главе были описаны две важные характеристики систем - управляемос и наблюдаемость. Управляемость показывает, достаточно ли регулируемых парам ров, чтобы привести систему в заданную точку в пространстве состояний. НаблюД»

---------- ------„,т1ттпрНН1

мость показывает, можно ли на основе измеряемых величин найти все внутреНИ" переменные системы. Если технический процесс наблюдаем, то функция оценки" зволяет определить переменные состояния, которые не измеряются датчиками посредственно. Если на процесс или измерения влияет шум, то процедура оцен должна включать в себя модель возмущений, которая обычно базируется на их стаТ

стических свойствах.

Многими промышленными процессами можно управлять без количествейН математических моделей. Мысленные модели принятия решений (глава 11) котор

пользуются операторы, позволяют им управлять даже очень сложными система Если управляющий компьютер должен в той или иной степени имитировать 1 дель принятия решении человека, то систему управления необходимо описьвать 3 лингвистических терминах. Одним из средств описания моделей с внутренними неопределенностями служит нечеткая логика. "иими

Последовательностные системы и системы дискретных событий широко пойме няются в промышленности Некоторыми процессами можно управлять с помо,пк1~ относительно простых комбинационных сетей, для других - необходимо учитьшятТ их предыдущие состояния (историю). В этой главе были рассмотрены некоторые спо собы моделирования последовательностных систем.

Рекомендации по дальнейшему чтению

Существует много книг, посвященных моделированию динамических систем; не очень сложными введениями являются [Luenberger, 1979] и [Ljung/Glad, 1994]. Идентификация процессов и оценка параметров, которые были коротко затронуты ватой главе, - предмет рассмотрения [5о(ег5Ггбш/8Го1са, 1989] и [Ljung, 1987], которые рекомендуются как вводные, а [Ljung/Soderstrom, 1983] дает подробную информацию по рекурсивным оценкам.

Важным разделом механических систем является динамика и кинематика роботов; [Craig, 1989] дает короткое, но превосходное введение в эти вопросы. [Spong/ Vidyasagar, 1989] и [Asada/Slotine, 1986] представляют собой более полное рассмотрение задачи управления роботами.

Много книг посвящено электрическим системам. [Eitzgerald/Kingsley/ Umans, 1990] - это стандартный учебник по электрическим машинам; [Mohan/ Undeland/Robbins, 1995] дает обзор перспектив силовой электроники. Динамичес-кимаспектам особое внимание уделено в [Leonhard, 1985]. [Elgerd, 1982] предлагает хорошее введение в электрические системы.

[Kreutzer, 1986] представляет собой обзор математических методов для моделирования зданий; в книге даются различные стили моделирования и соответствующие методы расчетов на компьютере.

[Wolfrara, 1991] - это известный справочник по пакету Mathematica. [Buckley, 1964] - классическая книга о моделировании и управлении химическими процессами. Представление об этих процессах также можно получить LEuyben, 1990], где приведено несколько иллюстраций моделирования техно-ии химических процессов. [Seborg/Edgar/MelHchamp, 1989] дает подробное ванп"" управления химическими процессами. Некоторые аспекты моделиро-al 100"**** биологической очистки сточных вод можно найти в [Henze et Тепла [Olsson, 1985]. [Cannon, 1967] обсуждает в деталях процессы передачи

вне""/"™" 986] рекомендуется как превосходное введение r,Q Рвпые системы управления. [Кио, 1995] содержит большой вводный раздел аи, лированию физических систем и описание необходимой математики для их Ле„ дискретные как детерминированные, так и стохастические системы управ-urk "°Р°™ излагаются в [Astrom/Wittenmark, 1990] и [Franklin/Powell/ 5q н, 1990]. В обеих книгах детально рассматривается влияние интервала вы-На устойчивость системы.