sm если

21.x

(3.7)

«1, или «л:. (3.8)

Подстановка уравнения (3.7) в уравнение (3.6) приводит к формуле

Р=9си[]. • (3.9)

Уравнение (3.9) относится к дальнему полю, где р изменяется обратно пропорционально х.

Ошибки приближений (3.4) и (3.7) приведены на рис. 3.14а и 3.146. Из этих рисунков видно, что рассматриваемый критерий зависит от выбора приемлемой погрешности. В общем случае минимальное значение х на высоких частотах определяется приемлемой ошибкой на рис. 3.146. Расстояние х уменьшается с понижением частоты и на низких частотах достигает постоянной величины, определяемой приемлемой ошибкой на рис. 3.14а. Для случая а=10 см это иллюстрируется рис. 3.15, где каждая прямая соответствует одному из указанных критериев. В точках пересечения прямых и вблизи этих точек максимальная ошибка равна сумме двух ошибок.

Стандартные критерии минимального расстояния для круглых поршней имеют вид [6]

хш1К (3.10)

ха. (3.11)

но часто используются другие критерии, показанные на рис. 3.14 и 3.15.

Имеются два критерия близости, поскольку волны характеризуются двумя параметрами-фазой и амплитудой. Критерии в уравнениях (3.5) и (3.11) и кривая ошибок на рис. 3.14а не зависят от длины волны и связаны с требованиями к амплитуде. Критерии в уравнениях (3.8) и (3.10) и кривая ошибок на рис. 3.146 связаны с требованиями к фазе.

Критерии для преобразователей, отличных от круглого поршня, выводятся аналогичным образом. Однако в тех случаях, когда форма преобразователя не является простой - кругом, квадратом, прямой линией и т. д.,- непосредственное вычисление может оказаться невозможным. К счастью, опыт показывает.

В качестве второго приближения мы используем выражение sin 9 - 6, справедливое для малых углов, т. е.

ita2

что относительно формы преобразователей можно делать довольно свободные допущения.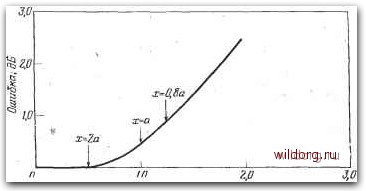

Рис. 3.14а. Ошибка, возникающая при учете только первых двух членов

в биномиальном разложении выражения (х+аУ. Кривая соответствует

формуле

. 201g- + 2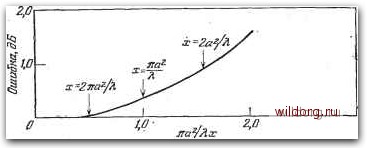

J.17

Рис. 3.146. Ошибка, возникающая при замене синуса его аргументом: Кривая

соответствует

7tfl2/2Xx sln(M2/2Xx) •

Для квадратного поршня критерий имеет вид xw/k, где W - длина стороны квадрата. Критерий для квадрата и уравнение (3.10) для круга можно объединить выражением

л:>-=№, (3.12)

которое используется для однородных .поршней любой формы (шестиугольник, восьмиугольник и т. д.), близкой к квадрату или кругу.

У неоднородных поршней амплитуда скорости обычно распределяется по поверхности таким образом, что максимум амплитуды находится в центре, а к краям она постепенно уменьшается. Можно считать, что эффективный диаметр или ширина

0.Б 0,4

0.1

£,06

€,02

W БО

Б 8 10

Рис, 3.15. Минимальное расстояние х между круглым поршнем радиуса а и точечным преобразователем согласно критерию минимального расстояния, указанному на каждой прямой. Д - максимальная ошибка, дБ; а=0,1 м; %=

c/f= (1500 м/с) .

таких поршней равны расстоянию между точками, где амплитуда уменьшается до половины максимального значения. Если не известно, по какому закону спадает амплитуда, то разумнее всего считать амплитуду постоянной.

Критерии для линийили тонких цилиндров имеют вид

xLIK . (3.13)

л>1, (3.14)

где L - длина линии. Неравенства (3.13) и (3.14) сами по себе имеют ограниченное применение, но они полезны тем, что легко