Рис. 3.45. Типичный эффект газового пузыря в воде вблизи гидрофона (показан пунктирной кривой).

(типа той, что показана на рис. 3.45), для того чтобы убедиться, является ли эта кривая истинной характеристикой преобразователя или аномалия на ней вызвана пузырьком в среде. Поскольку резонансная частота пузырька зависит от статического давления, то при изменении глубины частота аномалии сдвинется. Однако такую проверку нельзя считать однозначной, поскольку пузырек может находиться внутри чувствительного элемента преобразователя, в частности в среде, которая акустически связывает пьезокристалл с водой. Важно иметь представление о том, как воздушные пузырьки влияют на результаты гидроакустических измерений.

Рассмотрим пузырек с малым радиусом по сравнению с длиной звуковой волны в воде. Пузырек находится в свободном звуковом поле с давлением pf. Акустический импеданс самого пузырька состоит из гибкости С заключенного в нем газа и сопротивления R, возникающего из-за потерь при сжатиях и расширениях газа. Масса движущегося газа пренебрежимо мала. Эквивалентную схему для пузырька в воде, возбуждаемого звуковым давлением, можно составить на основе теоремы Тевенина. Давление, действующее на затормо5кенный пузырек (или давление холостого хода), можно определить, полагая им-

диаметром 1 см, расположенный вблизи поверхности, при атмосферном давлении имеет резонанс на частоте 667 Гц [16]. Зная эту частоту и пользуясь указанными выше зависимостями, можно вычислить резонансную частоту более мелких пузырьков при разных давлениях. Пузырьки обычно малы в сравнении с длиной волны, и, следовательно, их форма не играет роли. Поэтому можно полагать, что резонансная частота пузырьков других форм примерно равна резонансной частоте сферического пузырька такого же объема.

Маленькие газовые пузырьки могут быть цепкими и устойчивыми. Поэтому необходимо внимательно исследовать и проверять аномалий на записанных экспериментальных кривых

педанс пузырька близким к бесконечности. Если пузырек мал, это давление равно давлению в свободном поле. Затем выключаем генератор и оцениваем импеданс на зажимах генератора. Это значит, что мы смотрим на генератор со стороны нагрузки, или, говоря языком акустики, смотрим -в среду из пузырька и видим импеданс излучения R+jcom. Для маленького сферического излучателя (nmR. Таким образом, мы получаем эквивалентную схему, показанную на рис. 3.46. Здесь и - скорость смещения поверхности сферического пузырька, и положительным считается направление внутрь.

/77- Р

ллл-

Рис. 3.46. Эквивалентная схема газового пузырька в воде, возбуждаемого давлением свободного поля pf. т - присоединенная масса воды; R - сопротивление газа в пузырьке и сопротивление излучения; С - гибкость газа в пузырьке; и - линейная скорость поверхности пузырька. За положительное направление отсчета принято направление внутрь пузырька.

Схема на рис. 3.46 является обычным последовательным резонансным контуром. При постоянном Pf относительная амплитуда и фаза и пропорциональны адмитансу пузырька, показанному на круговой диаграмме на рис. 3.47. Предположим, пузырек и гидрофон расположены близко друг к другу, так что расстояние между ними удовлетворяет условию г<СХ. Пусть, пузырек находится сбоку от гидрофона, так что давление свободного поля в месте их расположения одинаково по амплитуде и фазе. Это условие соответствует прилипанию пузырька к чувствительному элементу гидрофона. Тогда полное давление рн в месте расположения гидрофона и вблизи пузырька равно сумме Pf и давления рг, излучаемого пульсирующим пузырьком, как показано на рис. 3.48.

Пузырек ведет себя как точечный сферический излучатель, и давление рг можно вычислить по одной из известных формул, например pr=j(i)pU/r, где U - объемная скорость. Это значит, что нагрузкой излучения служит реактивность массы и рг опережает на 90°. скорость, направленную наружу. Поскольку за положительное направление скорости мы выбрали направление

внутрь, то рт опережает отрицательную скорость на 90° или положительную-на 270°. Следовательно, годограф Рг относительно Pi получается поворотом круга, показанного на рис. 3.47,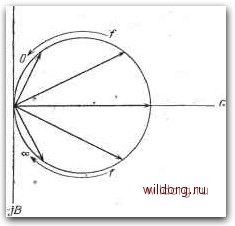

f=fg (резонанс

Рис. 3.47. Адмитанс последовательно соединенных массы.иг, сопротивления R и гибкости С. «~ y=G-f/B=[/?-f;(coM-I/coCm)]-.

на 270°. На резонансной частоте скорость и зависит от R, и отношение pripf зависит от Q резонансной системы и расстояния г. Значит, сумма рн=р1+рг меняется, как показано на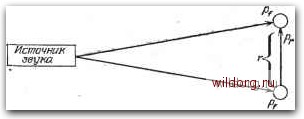

Пузырек

Рис. 3.48. Положение, при котором давление свободного поля воздействует и на гидрофон и на газовый пузырек, находящиеся друг от друга на расстоянии г. Звуковое давление рг, переизлученное или рассеянное пузырьком, также воздействует на гидрофон.

рис. 3.49. Отметим, что резонансная частота не соответствует частоте максимального или минимального давления и частоте, при которой

Из рис. 3.49 видно, что отношение pulpf меняется с частотой, как показано на рис. 3.45. Если г увеличивается, то размер круга уменьшается и фаза рг изменится. Фазовый угол р,- равен -kr рад. Увеличение расстояния приводит к большему отрица-