6.5. МОДУЛИ УПРУГОСТИ И ЖЕСТКОСТЬ

Рассмотрение акустических материалов было бы неполным, если бы мы не упомянули модули упругости. В разд. 6.4 жесткость и модуль упругости для поршневой деформации считались синонимами. Такое определение удобно для одномерного анализа в случае плоской волны.

At/Z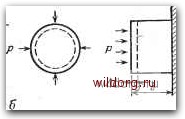

-I I

ш7777777777777

Рис. 6.10. Модули упругости. а - модуль Юига У и коэффициент Пуассона а: F - сила, А - площадь.

/ - длина, t - толщина, Y=

Mil •

•6 -модуль всестороннего сжатия В: р -давление, V-объем, В= дуД/

S - модуль для поршневой деформации Р: р - давление, / - длина, Р=щ, г - модуль сдвига р,: F-сила. At - площадка, на которую действует

сила F,v - угол сдвига в радианах, ц= -g- .

В твердом теле имеется несколько способов приложения напряжений и возникновения деформаций, и каждая комбинация имеет свой собственный модуль упругости или жесткость (или гибкость). На рис. 6.10 показаны эти модули.

Модуль Юнга У, вероятно, наиболее известен, и его легче всего измерить. Он относится к длинному тонкому твердому телу (проволока, стержень и т. д.). В акустических измерениях или приложениях «тонкий» означает: поперечный размер составляет малую долю длины волны. Тогда напряжение существует лишь в одном направлении - направлении оси стержня - и задается силой, действующей на единицу площади, или давлением.

Деформация происходит в трех измерениях, но определяется только в направлении оси стержня. Воздействие напряжения изменяет и объем, и форму материала.

Модуль всестороннего сжатия В является мерой отношения между трехмерным напряжением и трехмерной деформацией. Изменяется объем, но не форма. Так, например, резиновый мяч, сжимаемый со всех сторон, становится меньше, но сохраняет сферическую форму. Напряжение задается давлением, а деформация- относительным изменением объема.

Модуль Р для поршневой деформации обычно используется при измерениях в импедансной трубе или в условиях плоской волны. Напряжение или давление прикладывается только в направлении волнового движения. Деформация, или движение частиц, происходит в направлении действия напряжения. Этот модуль в большей степени, чем другие модули, применим к динамическим случаям. Как и в случае модуля Юнга, с приложением напряжения меняются и объем, и форма.

Модуль сдвига или кручения р, относится к вращательному движению. Объем остается постоянным, но форма меняется. Напряжение задается в виде тангенциальной силы, действующей на единичную площадку по касательной к поверхности. Деформацией является угловое смещение в радианах первоначально перпендикулярных граней. Модуль сдвига важен для поглотителей, так как резины часто имеют составляющие с малыми потерями в «пластинчатой» жесткости и составляющие с большими потерями в «сдвиговой» жесткости.

На практике условия измерения, форма и размер образца материала могут привести к возникновению напряжений и деформаций, которые связаны совокупностью всех четырех модулей. Поэтому нужно осторожно относиться к экстраполяции результатов измерений на образцы других форм и размеров.

Кроме модулей, для характеристики упругих свойств материала часто используют коэффициент Пуассона. Как видно из рис. .6.10. а, он выражается отношением возникшей поперечной деформации к созданной продольной.

.Модуль всестороннего сжатия, модуль сдвига и модуль для поршневой деформации связаны с модулем Юнга и коэффициентом Пуассона а следующими формулами:

. (6.48)

Р= ,Х + 1Н1% . (6-49)

Литература

1. Татт К., Broad-Band Absorbers Лог Water-Borne Sound, in Teclmical As-

pects of Sound, ed. E. G. Richardson, Vol. II, Elsevier Publ. Co., New York, 1957, Chap. 6.

2. Cramer W. S., Bonwit K. S., Pulse Tube for Acoustic Measurements, U. S.

•Naval Ordnance Lab. Rep. NAVORD 2257, 30 Apr. 1952.

3. Beranek L. L, Acoustic Measurements, John Wiley and Sons, New York,

1949, Chap. 7. (Русский перевод: Беранек Л., Акустические измерения, ИЛ, М., 1952.)

4. Zwicker С, Kosten С. W., Sound Absorbing Materials, Elsevier Publ. Co.,

New York, 1949, Chap. V. (Русский перевод: Цвикер К-, Костен К-, Звукопоглощающие материалы, ИЛ, М., 1952.) . .

5. Meyer Е. et al., Sound Absorption and Sound Absorbers in Water, NAV-

SHIPS 900,166, U. S. Department of the Navy, Washington, D. C, 1950.

6. Sabin G. A., Analysis of Acoustic Impedance Data, Navy Underwater Sound

Reference Lab. Res. Rep. № 81, 5 May 1966 [AD-632 075].

7. Sabin G. A., Acoustic Impedance Measurements at High Hydrostatic Pres-

sures, J. Acoust. Soc Am., 40, 1345 (1966).

8. Lastinger I. L.. Sabin G. A., A PDP-8 FORTRAN Program for Reduction

of Acoustic Impedance Data, Naval Res. Lab. Rep. 6906, 28 Mar. 1969 [AD-686 663].