При использовании метода DRL для измерений в импульсном режиме требуемый объем воды, вероятно, достигает практического минимума. Только изобретение идеального звукопоглощающего покрытия, которое позволило бы исключить по-

Преобра-зоватвль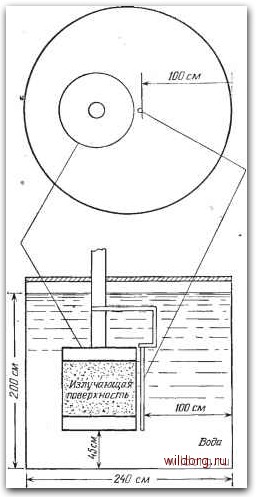

Линейный гидрофон

Воздух

Рис. 4.8. Расположение цилиндрического преобразователя в тонкостенном

стальном баке [7].

мехи, связанные с отражениями от границ, могло бы еще более уменьшить требуемый объем воды. На рис. 4.8 показаны размеры водоема, который использовал Бейкер. Диаметр бассейна превосходит диаметр преобразователя менее чем в 3 раза.

4.4. ПРИНЦИП РЕШЕТКИ ТРОТТА

Тротт [8, 9] В своих первых исследованиях методов градуировки в ближнем поле заметил, что звуковые давления, создаваемые большим поршневым излучателем в ближнем и дальнем полях, связаны так же, как параметры взаимности для сферической и плоской волны (см. разд. 2.3.1 и 2.3.5). Действительно, если один и тот же преобразователь является точкой в сферической волне (как предполагается при градуировке стандартным методом взаимности для сферической волны) или плоскостью в плоской волне (как предполагается при градуировке

Преабраза- Усредиетое давление ватель в ближнем mm

\ \

I I

Давление в дальнем поле

-Pff

Рис. 4.9. Ближние и дальние поля поршневого преобразователя. Sp = pnfli,

Ss = Pffli.

методом взаимности для плоской волны), то его чувствительность по напряжению в свободном поле М в обоих случаях будет одинаковой. Но чувствительность преобразователя в режиме излучения S зависит от вида колебаний и от того, на каком расстоянии она определяется. Таким образом,

7H=Vp=V.. (4.5)

где / - параметр взаимности, а индексы р и s относятся соответственно к плоской и сферической волнам. Ближнее поле большого круглого поршневого излучателя, как видно из рис. 4.9, по-сушеству состоит из. коллимированного пучка звуковой энергии. Среднее значение звукового давления р-п/ в любом поперечном сечении ближнего поля равно постоянной величине; следовательно, ближнее поле аппроксимируется коллимированным пучком однородных плоских бегуших волн [10, 11]. Звуковое давление в дальнем поле рц, создаваемое тем же большим круглым поршневым преобразователем при таком же токе возбуждения, как следует из формулы (4.5), связано с давлением pni соотношением

(4.6)

где Vl-опорное расстояние при определении Ss, % - длина волны, S - площадь поперечного сечения пучка.

Используя аналогичные рассуждения и вводя параметр взаимности для цилиндрической волны (разд. 2.3.4), можно показать, что отношение давления дальнего поля к давлению ближнего поля для линейного или тонкого цилиндрического преобразователя равно Lrzlryk, где гг - опорное расстояние при определении чувствительности преобразователя, излучающего цилиндрические волны, L - длина линейного преобразователя.

Как и в методе DRL, среднее значение звукового давления в ближнем поле определялось путем применения техники сканирования 1 интегрирования при помощи точечного или линейного гидрофона.

Применение параметра взаимности фактически эквивалентно особому случаю метода DRL, или метода Кирхгофа-Гельмгольца. Если в уравнении (4.4) мы примем cosp=l, модуль интеграла станет равным

J f2/7(Q)rfS=2p„/S (4.7)

\p{P)\\Pff\-PnfS, (4.8)

Pff\Pnf=S\r,\. (4.9)

Соотношение (4.9) совпадает с (4.6).

Вместо того чтобы от частного случая применения формулы Кирхгофа-Гельмгольца, или метода DRL, с их расчетными проблемами перейти к более общему случаю, Тротт поступил иначе. Он поменял ролями излучатель и гидрофон и представил сканирующий преобразователь как точечный источник, который при интегрировании за некоторый период времени должен создавать плоскую волну согласно принципу Гюйгенса. Если бы плоская сканируемая площадь была достаточно большой, то проинтегрированное звуковое давление, воздействующее на градуируемый преобразователь, невозможно было бы отличить от звукового давления в плоской бегущей волне. Следовательно, вопрос надо поставить так: насколько велики должны быть размеры плоской сканирующей площади, чтобы они удовлетворяли данному условию? При решении этого вопроса Тротт решил обойтись без сканирования и расчетного интегрирования, задумав создать большую многоэлементную решетку, составленную из малых источников звука. Каждый элемент этой решетки, являющийся точечным источником звука, должен создавать элементарные волны Гюйгенса. Элементы решетки должны быть достаточно малы и в то же время достаточно удалены друг