140 Гл. UI. Основы измерений в свободном поле

минимального расстояния, или близости, зависят как от размера и формы обоих преобразователей, так и от требуемой точности и вида измерений.

Критерий минимального расстояния для одиночного излучателя вытекает из требования, содержащегося в определении чувствительности .по току или по напряжению: давление должно соответствовать сферически расходящейся волне. Опорное расстояние принимается равньш 1 м от излучателя. Если на расстоянии 1 м волна еще не является сферически расходящейся, то нужно измерить звуковое давление на большем расстоянии и экстраполировать его назад к 1 м, предполагая, что давление изменяется обратно пропорционально расстоянию.

Критерий минимального расстояния для гидрофона вытекает из определения чувствительности по напряжению в свободном поле - при этом входное давление свободного поля обусловлено давлением в плоской бегущей волне. Плоские волны в свободном поле можно получить лишь приближенно, так что практически требуется, чтобы гидрофон пересекал участок сферической волны, который неотличим от волны плоской. Иными словами, этот участок должен быть очень малым или радиус кривизны волны должен быть очень большим.

Вопрос о выборе достаточного расстояния между излучателем и гидрофоном можно решить экспериментально. Для этого нужно измерить выходное напряжение гидрофона на двух или более расстояниях при постоянном токе излучателя. Если напряжение изменяется обратно пропорционально расстоянию, то критерий минимального расстояния выполняется. Но если такая пропорциональность не обнаружена, то это еще не означает, что вопрос решен отрицательно, так как нарушение закона об-ратной пропорциональности может быть связано с другими причинами, а не с влиянием близости. В этих случаях, а также при планировании и проектировании измерений критерии минимального расстояния и понимание эффектов близости весьма полезны.

В литературе [4-7] приводятся критерии минимального расстояния для преобразователей простых форм типа поршней и линий. Эти критерии .применимы к одиночным излучателям, в том смысле, что они определяют расстояние, на котором кончается зона Френеля, или ближнее поле, и начинается зона Фраунгофера, или дальнее поле. К системе излучатель-гидрофон эти критерии пригодны лишь в том случае, если гидрофон можно считать точечным. Если ни излучатель, ни гидрофон нельзя считать точечными, то нужно устанавливать критерий для конкретных комбинаций преобразователей. Этот критерий не является просто суммой критериев для каждого из двух преобразователей. Хотя критерий минимального расстояния обычно

устанавливает расстояние, на котором начинается сферически расходящееся дальнее поле излучателя, его можно применять также и для преобразователя, используемого в качестве гидрофона. Например, из теории взаимности очевидно, что критерий близости для комбинации большого поршня и маленького точечного преобразователя должен быть тем же самым независимо от того, что из них служит излучателем, а что гидрофоном.

Комбинация большого круглого поршня и малого точечного преобразователя является простым и удобным примером для выяснения смысла критерия минимального расстояния.

рз:= const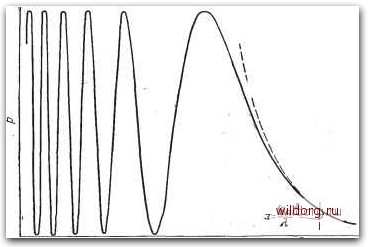

Рис. 3.13. Относительное изменение давления р в зависимости от расстояния X на оси круглого поршневого излучателя радиуса а для звука с длиной волны Я. Так же изменяется давление, усредненное по площади круглого поршневого гидрофона радиуса а в свободном поле точечного излучателя, расположенного на расстоянии х по оси гидрофона. Шкала х логарифмическая.

Если большой поршень служит излучателем, то звуковое давление на оси поршня, измеренное точечным гидрофоном, изменяется, как показано на рис. 3.13. Штриховая кривая, иллюстрирующая закон обратной пропорциональности давления дальнего поля, очень плавно сливается со сплошной кривой. Это показывает, что между ближним и дальним полями нет резкой границы. Поэтому не удивительно, что критерии минимального расстояния, приводимые разными авторами, не всегда согласуются между собой.

Если бы большой поршень был гидрофоном, а точечный преобразователь - излучателем, расположенным на оси поршня, то волны, падающие на поршень, были бы больше похожи на сферические, чем на плоские. Амплитуда давления на краю

поршня была бы меньше, чем в середине, и давление менялось бы по фазе при движении от центра к краю. Ясно, что давление свободного поля, усредненное по поверхности поршня, должно быть меньше, чем давление на оси диафрагмы поршня. Если это среднее да.вление свободного поля представить графически в зависимости от положения излучателя на оси, то форма кривой была бы идентична форме кривой на рис. 3.13. Критерий минимального расстояния для поршневого гидрофона такой же, как и для поршневого излучателя.

Критерий минимального расстояния для круглого поршня в жестком экране определяется путем анализа выражения для давления на Ъси:

(3.1)

где р - плотность воды, с - скорость звука, и - скорость поршня, к=2п1к - волновое число, Я, -длина волны, х - расстояние по оси от поршня до точки наблюдения, а - радиус поршня.

В дальнем поле уравнение (3.1) можно упростить:

/ м2\

(3.2)

Математически критерий минимального расстояния связан с вопросом о степени приближений, которые необходимо сделать, чтобы свести уравнение (3.1) к (3.2). Это следующие приближения.

Член {х+.ау/ можно разложить по формуле бинома в бесконечный ряд:

2х 8x3

(3.3)

и учесть только первые два члена ряда. Таким образом, приближение

4 (3-4)

верно лишь в том случае, когда а2 а4

« 2.

(3.5)

Подставляя (3.4) в уравнение (3.1), получим

р=2рси sin

=2рси sin

(3.6)