где р - среднеквадратичное значение звукового давления, и - среднеквадратичное значение колебательной скорости частицы, р1-мгновенное значение звукового давления, dpi/dx - градиент давления в точке х в направлении оси х, ш - круговая частота, р - плотность, с - скорость звука.

Из этих соотношений видно, что при фиксированном давлении р, зависящем от частоты ш, колебательная скорость частицы и будет также постоянной, однако градиент давления dpi/dx будет пропорционален частоте. Из уравнения (5.16) можно также заметить, что градиент давления и колебательная скорость сдвинуты друг относительно друга по фазе на 90°." Таким образом, если мы определяем гидрофон колебательной скорости как такой гидрофон, у которого выходное напряжение пропорционально и, то его чувствительность по напряжению в свободном поле будет постоянной, или, другими словами, егО частотная характеристика будет плоской. С другой стороны, если гидрофон градиента давления определить как гидрофон, у которого выходное напряжение пропорционально градиенту давления, то его чувствительность по напряжению в свободном поле будет пропорциональна частоте, т. е. частотная характеристика будет иметь наклон 6 дБ/октава.

нулевого порядка является ненаправленным. На практике термин «градиент давления» означает градиент давления первого порядка, если не оговаривается другое значение.

Использование дипольного преобразователя - это практически единственный метод получения хотя бы умеренной направленности на низких и средних звуковых частотах, если не обращаться к крупногабаритным преобразователям. Обычно-понятия «гидрофон градиента давления» и «гидрофон колебательной скорости» считаются равнозначными, однако между этими двумя типами гидрофонов существует различие.. Это различие относится к предсказываемой частотной характе-ристике, о чем полезно помнить тому, кто применяет или градуирует такие гидрофоны.

Большинство гидрофонов градиента давления и колебательной скорости состоят из какого-либо чувствительного элемента, который совершает колебательное движение под влиянием градиента давления или колеблется вместе с частицами воды.

Зависимость между давлением, колебательной скоростью и градиентом давления в плоской бегущей волне определяется следующими соотношениями:

р=рси, (5.15)

-=-ywpff=-y-A . - (5.16)

Поскольку наклон характеристики чувствительности гидрофона зависит как от принципа преобразования, так и от механического импеданса колеблющегося элемента,, то обычно один и тот же гидрофон является гидрофоном градиента давления в диапазоне ниже резонансной частоты и гидрофоном колебательной скорости на частотах выше резонанса. Следовательно., существующие термины имеют вполне определенный смысл.

Колебательная скорость и градиент давления заставляющие чувствительный элемент совершать колебательные движения, не обязательно равны колебательной скорости частиц и градиенту давления в плоской бегущей волне. В конструкции гидрофона прежде всего стараются каким-либо путем акустически усилить колебательную скорость волны или градиент давления, чтобы усилить их действие на гидрофон на частотах вне области резонанса.

Градуировка гидрофонов градиента давления и колебательной скорости производится в единицах звукового давления плоской волны, т. е, так .же, как гидрофонов давления. Когда в некоторых особых случаях необходимо использовать в качестве единицы колебательную скорость плоской волны, частотную характеристику получают за счет добавления 20 Igpc, или 103,5 дБ..

5.12.1. Гидрофоны колебательной скорости

Обычный широкополосный гидрофон колебательной скорости работает по принципу электрогенератора, который генерирует" напряжение е, когда провод (обычно катушка) длиной L пересекает со скоростью Uc магнитное поле, имеющее индукцию В, что соответствует уравнению

e=BLu,. (5.17).

Один из типов гидрофона колебательной скорости подобен электродинамическому преобразователю, за исключением того, что звуковое давление воздействует на противоположные стороны или концы катушки, причем давление, заставляющее катушку перемещаться, равно разности мгновенных значений давлений Др,- Эта разность давлений равна градиенту давления в звуковом поле, умноженному на разность акустического пути Ах между двумя сторонами или концами катушки, на которую воздействует звуковое поле, и на cos О (рис. 5.39). Следовательно,

; Др.=Д;ссо5е. (5.18>

Подставляя уравнение (5.16) в (5.18), получаем • ДА=-у(-)/?Дхсо5е. (5.19)

Как было показано экспериментально, величина разности акустического пути Ах довольно точно соответствует физическим размерам пути в обход экрана, окружающего катушку.

Частное Арг/ис зависит от удельного акустического импеданса катушки и от ее подвески. Подвеска катушки должна быть чрезвычайно мягкой, чтобы резонанс подвески и массы катушки располагался ниже рабочего диапазона частот, выбранного равным, например, 50-100 Гц. Тогда импеданс фактически равен

Jteeiwu каркас и прозрачный корпус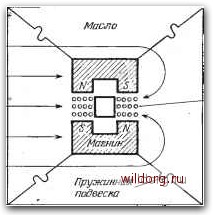

-50мМ

Катушка иа -пластмассовом сердечнике

Рис. 5.40. Поперечный разрез гидрофона BTL типа 1А в горизонтальной плоскости (упрощенная схема). Здесь й далее параллельными стрелками изображено звуковое поле.

реактивному сопротивлению /сот катушки и присоединенной .массы воды и

hpi jam

(5.20)

где 5с - площадь катушки, на которую воздействует звуковое давление.

Из соотношений (5.17), (5.19) и (5.20) можно получить чувствительность по напряжению в свободном поле е/р:

BLSc Ах cos 6

Формула (5.21) показывает, что чувствительность не зависит от частоты и пропорциональна cos 0.

Первым гидрофоном колебательной скорости такого типа «был, вероятно, гидрофон 1А фирмы «Белл телефон лэборэтриз»