OA. иоъемные поглощающие материалы 341

I-,

что а=0,2 дБ/см, или 0,023 Нп/см. Ошибка здесь обусловлена тем, что сигнал отражается на обеих границах твердого тела с водой и при каждом отражении реверберирующего в пластине звука от передней и задней границы часть звуковой энергии уходит в воду. Следовательно, внутри пластины выполняются условия существования стоячей волны, и проходящая волна состоит из фазовой суммы многих сигналов, которые пересекли 5-сантиметровый слой 1, 3, 5, 7 и т. д. раз.

На практике а, г] и б обычно измеряются в импедансной трубе, схематически показанной на рис. 6.7. Труба рассматривается как одномерная передающая линия. Предполагается, что

Преобразователь

Поглотитель

Материал поВложки

Жесткие границы

Рис. 6.7. Схема импедансной трубы для измерения параметров поглощающих

материалов.

В трубе с жесткими стенками, диаметр которой составляет малую долю длины звуковой волны в воде или материале, распространяется плоская волна. * - Основным параметром, используемым для нахождения а, т] или б, является комплексный акустический импеданс Z, на границе между водной средой и поглощающей средой со стороны воды. Различные модификации импедансной трубы использовались главным образом в воздушной акустике [3, 4]. Наилучшим методом оценки подводных поглотителей Звука является эхо-импульсная методика [2, 5]. В ней измеряется комплексный коэффициент отражения А при отражении короткого звукового импульса от границы Zi. Модуль А равняется отношению отражен-, ного звукового давления к падающему. Фаза А выражается сдвигом фазы отраженного звука. Тогда

\. , =-4 :Л: (6-34)

1-.-

где Zw - удельный акустический импеданс воды. Абсолютную величину А относительно легко определить. Например, давление в падающем и отраженном импульсах в трубе можно измерять при помощи неградуированного линейного зондового гидрофона. Сравнивая амплитуды изображений импульсов на экране осциллографа, можно найти А. Фазу измерить труднее. Относительную фазу двух импульсов можно измерить на выходе зондового гидрофона, но фазовый сдвиг на границе вода-материал можно

ВЫЧИСЛИТЬ только при условии, что точно известны положение границы и длина звуковой волны в воде, заполняющец трубу.

Другой метод состоит в сравнении амплитуды и фазы сигнала, отраженного от образца, с амплитудой и фазой сигнала,, отраженного от идеального отражателя (такого, как высокоим-педансная или низкоимпедансная граница), расположенного-в том же месте. Измерив Zi и зная х я Z (импеданс на границе между поглотителем и следующим за ним материалом подложки), можно вычислить а, Г[ или б. Например, t\s можно-найти,выбирая x<X/10 и полагая Z-oo, т. е. используя тонкий слой поглотителя с жесткой подложкой. Тогда мы имеем условия, аналогичные измерению емкости и проводимости короткого отрезка разомкнутого кабеля. Поглотитель действует как. пружина с потерями,

Ri=sris\4x, (6.36>

Xi=slx. (6.37>

Из (6.36) и (6.37) можно найти s и Г[&.

Если нужно найти r\f, то, полагая л:<Я,/10 и Zj-D, мы используем тонкий слой без подложки или с воздухом в качестве подложки. Тогда мы имеем случай, аналогичный использованию-короткозамкнутого кабеля при измерении индуктивности и со- противления проводника. Поглотитель действует как масса, испытывающая вязкое сопротивление, и

г==г+У-/=У"рл:=>рд;-1-озр73рД;. (6.38>

Rim.x, (6.39>

Xi=px. (6.40>

Уравнения (6.39) и (6.40) можно решить относительно р и r\f.

Угол потерь 6 можно получить непосредственно из 2» в соответствии с (6.24).

Для измерения а подложка делается очень жесткой и предполагается, что Zl-oo. Тогда уравнение (6.11) сводится к виду

Zi=zUih{a-\-jk)x, (6.41 >

где -комплексный удельный импеданс материала. Из (6.13), (6.34) и (6.41), пренебрегая инерционн-ыми потерями, имеем 1. \+А cib{ax + jkx) ,„..

где индексом w "отмечены параметры, относящиеся к воде. Все параметры, расположенные в левой части (6.42), измеряются. Неизвестные а я k нельзя найти алгебраическими методами из трансцендентных уравнений типа (6.42). Однако Сэбин [6, 7] построил графики, по которым можно определить а и k, зная

- Иакзюи=-1 / т] р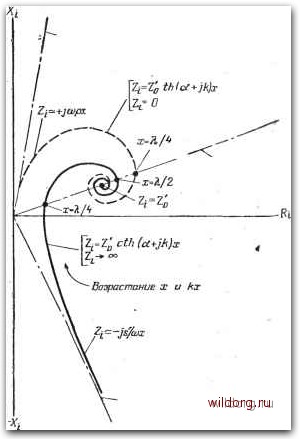

Рис. 6.8. Входной импеданс Zj акустической передающей линии с потерями в зависимости от длины kx (в радианах).

модуль И фазу левой части (6.42); впоследствии он использовал счетную машину для решения уравнения (6.42) автоматически методом последовательных приближений.

На рис. 6.8 приведен график уравнения (6.41)и, кроме того, уравнения (6.11) для частного случая Zi, = 0. Если Zj можно измерить в зависимости от л; и представить графически, как на рис. 6.8, то должна получиться спиральная кривая, по которой