I г

Рис. 4.11. Представление Z I суммарной функт(ии спадания с биномиальными коэф-/ 2 1 фициентами второй степени f 2 I вир.е комбинации шести линейных групп излучателей.

Для получения однородно распределенного давления в поперечном направлении, или вне оси, т линейных групп излучателей с биномиальными коэффициентами разложения устанавливаются параллельно друг другу через интервал, равный d. Тогда принцип суперпозиции в акустике позволяет утверждать, что интенсивности излучателей в каждом из положений суммируются, что показано на рис. 4.11, где число т взято равным 6. Диаграмма направленности т однородных точечных излучателей определяется уравнением (2.5) как (sin тф)/(т sin ф). Диаграмма направленности набора из m линейных групп излучателей, согласно теореме Бриджа, рассмотренной в разд. 2.11.1, выражается следующей функцией:

/W=-o"- (4.11)

При тф = 2я, 4я, 6я,... {sin пкр) I {т sin (р) =0. Боковые лепестки, как видно из рис. 2.42, имеют довольно большие амплитуды; следовательно, в диаграмме направленности, определяемой уравнением (4.11), также будут боковые лепестки, но за счет умножения на со8"ф их амплитуда будет уже меньше. Это иллюстрирует рис. 4.12 для случая п=2, т=6, d=K/2.

Полное отсутствие боковых лепестков не является обязательным оптимальным условием для получения лучшей однород-

группы излучателей с биномиальными коэффициентами спадания определяется функцией со8"ф, где ц>= (nd/X) sin0, d - расстояние между соседними источниками, 0 - угол на диаграмме направленности. Если d=U2, то ф= (n/2)sin0. Отсюда видно, что поскольку угол 0 меняется от О до 90°, то cos ф плавно уменьшается от Г до О, что свидетельствует об отсутствии в диаграмме направленности боковых лепестков. Функция совФ также будет плавно уменьшаться от 1 до О, и в диаграмме направленности, определяемой такой функцией, также не будет боковых лепестков. По мере возрастания числа п эта функция будет уменьшаться быстрее; при этом будет уменьшаться и ширина основного лепестка диаграммы направленности.

НОСТИ ближнего поля. На рис. 4.13 показано, как небольшие осцилляции давления в направлении акустической оси могут обеспечить на практике более широкую область однородного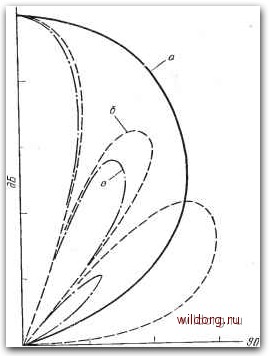

Рис. 4.12. Диаграммы направленности линейной группы точечных излучателей, разнесенных друг от друга на полдлины волны. а - для 3 излучателей, для которых спадание амплитуд определяется последовательностью чисел 1, 2, 1 (биномиальными коэффициентами разложения второй степени) и которые имеют характеристику направленности

р (e)=cos2(-7c sin ej;

б - для 6 излучателей с одинаковой амплитудой, имеющих характеристику

направленности

sin [6(1/2)sine] .

6Sin [гSin6]

е -для 8 излучателей, амплитуды которых спадают соответственно последовательности чисел 1, 3, 4, 4, 4, 4, 3, 1 (см рис. 4.11) и которые имеют характеристику направленности, равную произведению а и б.

давления, если на условие однородности наложить небольшие, но разумные ограничения. Для расширения области равномерного давления Тротт сохранил в диаграмме направленности

ОДИН небольшой боковой лепесток, или небольшие осцилляции давления в ближнем поле. Эффект расширения области однородного давления в такой же степени применим к поперечному направлению, как и к осевому. Оптимизация значений тип, заключающаяся в том, чтобы получить по возможности большую область плоской волны при допустимых отклонениях от однородного распределения давления, составляет главную проблему конструирования решетки Тротта.

Последовательность чисел, характеризующих относительные интенсивности излучателей, например 1, 3, 4, 4, 4, 4, 3, 1

Макс.

Макс.

Расстояние от акустической оси -

Рис. 4.13. Типичное изменение звукового давления вдоль оси круглого поршня, имеющего диаграмму направленности в дальнем поле без боковых лепестков (сплошная кривая) и с небольшими боковыми лепестками (пунктирная кривая). Стрелками показаны пределы допустимой неоднородности.

(рис. 4.11), представляет так называемую функцию спадания Тротта. Обычно эта функция дается нормированной к единице, так что последовательность чисел на рис. 4.11 будет выглядеть как 0,25; 0,75; 1,0; 1,0; 1,0; 1,0; 0,75; 0.25.

Конструкция плоской решетки создана на базе набора горизонтальных и вертикальных линейных групп излучателей. Применяя функцию спадания Тротта, как показано на рис. 4.14, получаем, что интенсивность каждого элемента в плоской решетке пропорциональна произведению f {х) f (у), где f (х) - значение функции спадания в горизонтальном направлении, f (у) - ее значение в вертикальном направлении. Если бы f (х) и f (у) были функциями Гаусса вида где k - постоянная и г - ра-

диальное расстояние, то в результате мы имели бы решетку с круговой симметрией интенсивностей излучателей. Для функции спадания Тротта круговая симметрия получается только приблизительно.

При рассмотрении конструкции в виде набора линейных групп излучателей предполагается, что ширина пространства однородного давления по крайней мере приблизительно соответ-