именно ограничение диапазона изменений амплитуды сигнала сверху.

Некоторые преобразователи гидролокационных станций возбуждаются сигналами с уровнями, превышающими диапазон, линейности. С возникающими, нелинейными эффектами (искажения и т. д.) мирятся, так как они менее важны, чем другие технические или экономические соображения. Испытания и градуировки можно проводить и с нелинейными преобразователями, но эти измерения имеют узкое применение. Формальные определения чувствительности по току в режиме излучения,, приемной чувствительности в свободном поле, импеданса, к. п. д. и т. д. относятся только к линейным преобразователям, и эти термины не имеют общепринятого значения при использовании-нелинейных преобразователей. Когда измерения проводятся с нелинейными преобразователями, должно быть указано абсолютное значение по меньшей мере одного из параметров (давление, напряжение или сила тока). Поскольку нелинейные искажения присущи всем нелинейным системам, то необходимо указать также, относятся ли данные только к основной частоте или же к суммарному сигналу из основной частоты и гармоник.. В общем случае условия измерений для нелинейных преобразователей Должны быть подробно уточнены, а результаты измерений нельзя экстраполировать на другие условия.

2.16. ИЗМЕРЕНИЯ ШУМА

Имеются два стандартных определения шума. Согласно первому из них, шум -это нежелательный звук. Так, например, если сигнал одного гидролокатора интерферирует с сигналом второго, то сигнал первого является шумом для второго, даже если он представляет собой синусоидальные колебания. Помеха от питания с промышленной частотой тоже является шумом. Согласно второму определению, шум представляет собой неустойчивое, прерывистое или статистически случайное колебание;.

Некоторые шумы могут быть неустойчивыми и прерывистыми, но при этом все же привязанными к некоторым дискретным частотам. Такой шум имеет линейчатый спектр (этот термин заимствован из оптической спектроскопии). Есть шум, имеющий непрерывный спектр, т. е. его частотные составляющие распределены непрерывно в некотором диапазоне частот.

При проведении измерений нас интересуют шумы в основном второго типа, и мы сосредоточим внимание на шумах с непрерывным спектром.

Можно предположить, что такие шумы являются наложением бесконечного числа синусоидальных сигналов с различны-Mir частотами и случайными амплитудами, распределенными

относительно некоторой средней амплитуды. Относительная средняя амплитуда каждой частотной составляющей зависит от типа шума. Если средняя амплитуда не зависит от частоты, то шум называют белым по аналогии с белым светом.

Амплитуда окружающего морского шума уменьшается на 5 дБ на октаву при увеличении частоты. В большинстве практических случаев амплитуда слабо зависит от частоты. Полная звуковая энергия в конечной полосе частот распределена по бесконечному числу частот. Звуковая энергия одной частотной компоненты исчезающе мала, и шум нужно измерять в некоторой полосе частот.

Звуковая энергия в полосе частот зависит от ширины полосы и от того, каким образом изменяются амплитуды частотных составляющих. Если шум является практически белым, то энергия пропорциональна ширине полосы. Среднеквадратичное давление в полосе акустического шума не имеет универсальной •связи со звуковой энергией. Однако в большинстве практических случаев квадрат среднеквадратичного давления (или среднее значение квадрата давления) пропорционален энергии и, следовательно, пропорционален также ширине полосы частот. Таким образом, акустический шум характеризуется среднеквадратичным значением квадрата давления и шириной полосы Af, в которой измеряется р. Спектральный уровень давления, или PSL, определяется формулой

P5Z.=201g(/7 7o)-101gA/. (2.107)

где Ро - опорное давление 0,0002 дин/см, а А/ - ширина полосы в герцах. Таким образом, PSL на частоте /о равно уровню среднеквадратичного давления относительно 0,0002 дин/см в полосе частот шириной 1 Гц со средней частотой fo. Обычно трудно проводить измерения в полосе 1 Гц, и, следовательно, 10 Ig Af больше нуля. Если шум не является практически белым, то измеряется среднее значение PSL. Выбор ширины полосы на практике обычно является компромиссным. Ширина полосы должна быть достаточно узкой, чтобы проследить изменения PSL в зависимости от частоты, но не настолько узкой, чтобы случайная мгновенная амплитуда шума могла стать достаточно большой и не позволяла измерить р точно. На рис. 2.56 показано, как выглядит шум на ленте самописца при записи белого шума через различные фильтры.

При электроакустических измерениях уровни шума измеряются для двух целей. Во-первых, может быть интересен сам акустический шум, например шум корабля. Для измерения шума необходим специальный измерительный прибор; градуировка его рассматривается в разд. 2.16.1. Во-вторых, интересен собственный шум измерителя или измерительной системы, по-

скольку он ограничивает минимальный измеримый уровень сигнала или указывает нижний предел динамического диапа-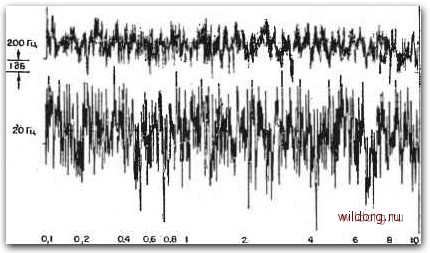

Рис. 2.56. Шумовой сигнал, записадный с помощью фильтра при ширине-полосы пропускания 6000, 200 и 20 Гц.

зона. Это ограничение обусловливается давлением, эквивалентным шуму, и рассматривается в разд. 2.16.2.

2.16.1. Градуировка измерителя шума

Измеритель шума можно отградуировать, помещая гидрофон в известное шумовое поле. Однако для определения характеристик шумового поля необходимо использовать другой образцовый прибор или измерительную установку. Иначе говоря, неизбежно возникает необходимость в одном из описанных в этой главе методов абсолютной градуировки гидрофонов, в непрерывном режиме. Допустим, что у нас имеется отградуированный гидрофон; рассмотрим шумоизмерительную систему, показанную на рис. 2.57. Электроакустический элемент гидрофона представлен генератором Тевенина с напряжением % и импедансом Z; eg=Mp, где М - известная чувствительность по напряжению в свободном поле, а р - неизвестное звуковое давление; ei представляет собой известное напряжение на