e=2/J

" i%inec?e. • (2.87)

Если, как мы предположили, диаграмма преобразователя неидеальна, то функция р (6) неизвестна и интеграл нужно вычислять графически или численными методами. Для выполнения графического интегрирования используется ряд вспомогательных средств, например один из двух бланков (рис. 2.48 и 2.49) [51]. По оси ординат откладывается величина [р {Q)/pof; разметка шкалы позволяет легко переносить значения этой величины (в дБ) с ленты записи диаграммы. По оси абсцисс откладывается значение угла 6 с интервалами, выбранными так, чтобы площадь, соответствующая произведению [р(е)/ро]е, была пропорциональна площади участка сферической поверхности при изменении 6 от О до 6, или интегралу

данный преобразователь хорошим приближением к какому-либо идеальному случаю, нужно измерить его диаграмму направленности и сравнить ее с рис. 2.41-2.43. Около 90% энергии, излучаемой идеальными поршнями и линиями, содержится в основном лепестке и около 95% -в основном и в первом боковом лепестках. Таким образом, если измеренная и теоретическая диаграммы в пределах ошибки измерения совпадают в области основного и первого бокового лепестков, то можно считать, что преобразователь удовлетворяет его математической модели. Это практическое правило справедливо в том случае, если ни один из боковых лепестков не является чрезмерно большим. Большой боковой лепесток в направлении 180°, или назад, особенно характерен для нежелательного и незапланированного излучения поршневых преобразователей.

Случай 2. Диаграмма направленности некоторых преобразователей: круговых поршней, цилиндров или линий - может быть неидеальной, но все же иметь ось симметрии. Это значит, что во всех плоскостях, проходящих через ось симметрии, диаграмма одинакова. Этот факт должен быть подтвержден непосредственным измерением нескольких диаграмм. Для интегрирования по всей поверхности dS выбирается так, как показано на рис. 2.47, и вычисляется интеграл

Jc?5=J2irr2sinec?e, (2.86)

где е - угол между опорным направлением или осью и направлением измерения. Если обозначить через p{Q) давление как функцию е, то из уравнений (2.81) и (2.86) можно получить Re-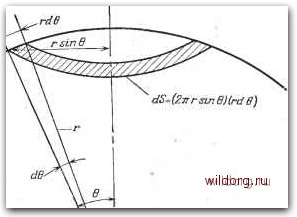

Рис. 2.47. Элементарный участок площади dS, используемый при интегрировании по сферической поверхности.

80 70 ео 50 W 30 20020 30 40 50 ВО 70 80 90°

Угол

Рис. 2.48. Бланк для определения направленности, излучения [51].

sin 9 dQ. После того как диаграмма нанесена на рис. 2.48 или

2.49, площадь под кривой измеряется планиметром. Если имеется излучение и в заднюю полусферу, то эту часть диаграммы нужно вычерчивать отдельно. Тогда определяется соотношением

2 (площадь переднего 4- площадь заднего бланков)

площадь под передней 4- площадь под задней кривой

(2.88)

10 о ю

30"

Рис. 2.49. Бланк для определения направленности излучения [51].

Даже если нет излучения в заднюю полусферу и знаменатель (2.88) равен площади под одной кривой, числитель все равно должен равняться площади двух бланков. Для остронаправленных диаграмм бланк, приведенный на рис. 2.49, более точен, чем на рис. 2.48; числитель (2.88) также должен равняться всей площади в пределах 09180°. Поэтому площадь бланка на рис. 2.49 должна быть увеличена в 7,46 раза, т. е. выражение (2.88) должно содержать дополнительный множитель 7,46.

Другим графическим средством является номограмма рис. 2.50 [50, используемая для получения приближенного