После некоторых алгебраических преобразований соотношение (6.26) можно упростить:

.р + \ 2a/fe

(6.27)

Уравнение (6.27) можно получить, используя вместо жесткости гибкость, или £=(1/рС)% и в уравнениях (6.29) и (6.30) используется обобщенный фактор упругих потерь це.

Тамм сделал свой вывод, используя r\s, а не rjc. Такой же вывод, как и в формуле (6.21), можно сделать при r]p=ns, при условии что r]s мало (если потери составляют малую часть импеданса или адмитанса).

6.4.3. Угол потерь б

Угол потерь б есть дополнительный до 90° угол фазы импеданса Zi, определяемого формулой (6.9):

tg8=/?,/X,. (6.22)

Если импеданс нагрузки Z-oo и толщина пластины мала или акустическай линия коротка (х<Я/10), то импеданс Zi управляется жесткостью и

Если импеданс нагрузки равен нулю и линия коротка, то импеданс управляется массой и

(6.24)

Таким образом, для малых образцов arctgrj и угол потерь - одно и то же.

6.4.4. Зависимость между а, т) и б

Прежде чем говорить об измерении а, г] и б, полезно узнать некоторые соотношения между этими параметрами. Во многих практических случаях, когда один параметр известен, можно вычислить или по меньшей мере найти приближенно два других.

Начнем с обычного выражения для скорости звука:

c=(s/p) или с=(1рУ\ (6.25)

Используя формулы (6.13), (6.14) и (6.16), можно найти

Р (1 - Яр) !/. . • (6.26)

Множитель a/k часто появляется при анализе поглощения. Кремер [2] обозначает его символом г и называет «параметром потерь»:

Можно видеть, что г в форме а%/2п есть затухание на 1 рад длины. После подстановки г в уравнение (6.27) оно принимает вид

Уравнение (6.29) является точным для любых значений затухания. Если затухание достаточно мало, так что можно пренебречь членами второго порядка, то из (6.29) получим

flpi-ri,=2raXj. (6.30)

Следовательно, г есть просто среднее значение величин щ и Tie.

Большинство материалов обладают в основном или упругими, или вязкими потерями, но не обеими одновременно. Если 1Г1р=0 или ifie=0, то (6.29) переходит в следующее соотношение:

•г=т- (6-31)

Если одновременно используется приближение малого затухания (6.30) и учитывается только один фактор потерь (6.31), то

,j=2r=aX/7r. (6.32)

Угол потерь 6 связан с т] соотношешями (6.23) или (6.24). при Г1<0,5 можно использовать приближение tg6?«6 с ошибкой менее 10%, и

tg88=--. -(6.33)

Справедливость предположения «малого затухания» и связи между г, 11 и б графически иллюстрируются рис. 6.6. Приведенные кривые являются графиками уравнений (6.31) и (6.32). Уравнение (6.30) нельзя представить графически, так как оно содержит три переменных. Из кривых видно, что 2r?«ri=«6 приблизительно при г<0,3 или г]<0,6. Значение г=0,3 соответствует затуханию 16,3 дБ на длину волны. Это значительное затухание. При длине волны 30 см г=0,3 соответствует а=0,6. Из этого можно заключить, что малые значения коэффициента затухания (а<0,1) и фактора потерь (ri<0,6) реальны и что приближение 2гУ]~б можно использовать в большинстве практических случаев.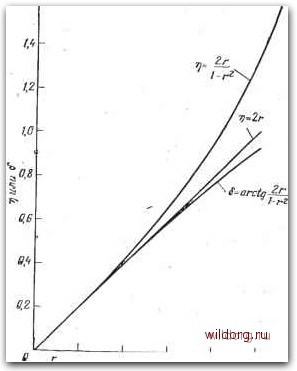

л-Л 5,5 10,9 оБ на длину волны

Рис. 6.6. Зависимость фактора и угла потерь от затухания на длину волны согласно уравнениям (6.31)-(6.33). r=ajk=a%l2n.

6.4.5. Измерение а, г] и б

Если излучатель и звукоприемник поместить в большой образец однородного поглощающего материала, то а можно измерить непосредственно по ослаблению сигнала в условиях свободного поля. Таким образом, потери в бегущей волне при распространении между двумя точками, сверх потерь на сферическое расхождение, можно приписать поглощению. Требования свободного поля ограничивают этот метод очень большими образцами, и по этой причине он используется редко.

Может показаться, что а можно определить просто по измерению звукоизоляции. Например, если звукоизоляция пластины толщиной 5 см равна 1,0 дБ, то можно заключить (ошибочно).