Уравнения электромагнитного поля

« l,257v (мкГн/м) и диэлектрической проницаемоч стью 8 = 8tier » 8,854ег [[пФ/м] волновое сопротивле"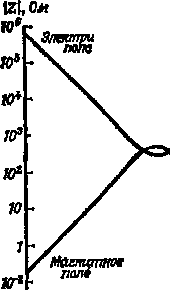

Плоская волна

ЯГЦ-I I , т 1

xf* да-* АГ J

Рис. 3.1. Волновые сопротивления электрического и магнитного полей.

ние можно выразить формулой

П = [;2я/р/(Г+/2фр)]=[Ом],

а постоянную распространения - формулой

<т = {;2я/1(1/р) + /2я/е]}

или в комплексном виде сг = я-}-/Р, где а - коэффициент поглоыения, а р - фазовая постоянная средЫ,,

Лрилчноние 3

Панетры щт а лозвотшют описать icnpocrpajtCHBe в данной среде любого .алек11{)оиагнитного лоля.

Пройдя в среде расстояние х [м], электромагнитное излучение ослабляется в ехр (а х) раз я приобретает сдвиг по фазе fix [радиан]. Кроме того, элекгри-.ческое и магнитное поля обмениваются энергиями,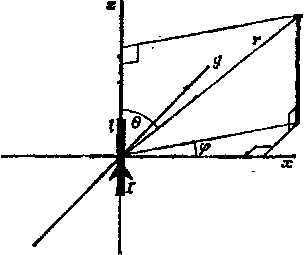

Рис. 3.2, Система координат для расчета излучения короткого диполя.

так что волновое сопротивление волны Z» стремится к т] по мере удаления от источника (рис. 3.1). У хороших диэлектриков р » оо, поэтому t » (р/е) и о «i »Дл/(pe)/*; следовательно, электромагнитное поле распространяется в диэлектриках без потери энергии. У хороших проводников р«0, поэтому 11« (я/цр)/2-}-+ 7ММР)" и юг « (n/ti/p)M2-f./(rtfft/p)/«. т. «. в проводящей среде электромагнитное излучение существенно ослабляется. Под толщиной скин-слоя понимают расстояние, на котором электромагнитное излучение ослабляется в е раз, поэтому 6 == 1/а =. = [р/(я/ц)]/2 [м].

На рис. 3.2 показан электрический диполь длиной /<Л./16, помещенный в диэлектрическую среду с магнитной проницаемостью ц и диэлектрической проницаемостью е, который нзлучает синусоидальные колебания с длиной волны Я, [м]. В точке со сфери-

ypavHMiM »1«ктромвгнитного поля 22)

чеегашш) ксюдинатами (г, ф, папряжеипоети влек* тричесхххго» я магнитного полей определяются* выражен ияш1

ег = f [ik/2arf - / {Я/2ягЛ cos 9 [В/м],

£е = "Г + (V2nr)*-/ (Я/2яг)1 sin 9 [В/м],

Яе=0,

Яф=(яЛД2>[/Л/2яг + (Л,/2яг)?}8аав.[А/14. "

В ближней зоне (г<Я,/2я [mJ электрическое поле максимально на осн z (9 = 0*, :±:180°), а маг< нитное поле -в плоскости ху{В = ±90**). 6 плоскости ху электромагнитная волна имеет волновое сопротив* ление (рис. 3.1)

" - Че А/2яг + (Я/2яг)» •

(1/8) [Ом! при. г :S. A2irc[#ii,

i (Л/е)"*А/2яг [ОмГ при г<л/Ъ1\к].

На ряс. ЗЛ показан небольшой контур площадью А (периметр 1<,%/2 fM]), находящийся в диэлектрической среде с магнитной! проницашоетью i и диэлеко трической проницаемостью е, по которому течет синусоидальный ток / е длиной волны к м], В точке со сферическими координатами (г, q?, в)) напряженности нолей рассчитываются по формулам

£, = 0, ее=щ £ф = g"Oi/;>/ 1 ; (x/2iwryi sin е fBr,

= Г/ (»./2itF)« -h (Л/2ягУ»1 cos e [AMI

tf6 = - ГЛ/2ЯГ - /• {%/2nrY - (Л/2яг)?1 sUi 6 [A/mJ,

Яф = 0.