\\\\\\\\

отдельных каскадов, варьируя R, позволяет добиться поглощения добавочного количества тепла между каскадами, отчасти компенсирующего выделение тепла Джоуля внутри их. Это обстоятельство и является причиной увеличения К и ДГах при применении каскадной системы охлаждения.

Рассмотрим процесс охлаждения с использованием л каскадов. Последовательность температур спаев обозначим через Го, Т„ Т, .... Т,, Т„

а величины протекающих через них теплот - Qq, Qj, Q2, •••

.. ,,Qi.....Q„ соответственно.

Такие обозначения возможны лищь в том случае, если выполнено условие стационарности процесса, согласно которому количество теплоты, выделяющееся на горячих спаях i-ro каскада Q,, должно поглощаться на холодных спаях /-f-l-ro каскада Qot+i-

/=1,2.....я-1. (6.1)

Интерес для изучения представляет главным образом величина К - общего холодильного коэффициента системы,

так как холодопроизводительность Qq целиком определяется режимом работы первого каскада. Вводя обозначения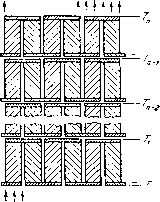

нииинн

Рис. 12.

U-l-l-i---- а-1-l-J-- Q

имеем очевидное тождество:

i=\, 2.

(6.2)

1 = 1

(6.3)

Равенство (6.3) связывает общий холодильный коэффициент системы К с холодильными коэффициентами каскадов Ki и сводит задачу о максимуме К к исследованию на минимум величины р-.

(6.6)

Такое исследование, однако, становится возможным лишь при соответствующей конкретизации температурной зависимости характеристической величины Ж(Г,

Ввиду этого, а также для удобства дальнейшего исследования, допустим, что в пределах температурного интервала (Tq, Т) ж = const. В некоторых случаях это допущение справедливо. Возьмем, например, материалы, для которых, согласно Юсти [30], справедлив обобщенчый закон Виде-мана - Франца,

kp = LT. (6.4)

где L - константа, отличная от идеального значения (для

-8 в*

металлов), равного 2,б-10 рад роме того, в инте-

ресующем нас интервале температур дифференциальная термо-э.д.с. пары а постоянна, то, согласно (5.29) и (6.4), имеем

а = ---=-= const.

Для термопар с непостоянным М приводимые ниже результаты будут справедливы лишь в известном приближении, однако соответствующий расчет показывает, что при небольших ДГ= Г„ - ГоьбО" точность этих результатов будет вполне удовлетворительной.

Строго говоря, наличие условий (6.1) превращает исследование [А на минимум в задачу об условном экстремуме, при решении которой эти условия должны существенно учитываться. Для удобства исследования мы отыщем сначала минимум jx как функции 2п переменных d. и d", на которые, кроме условий (6.1), накладываются еще дополнительные п условий вида

J[d.-i-pidl = Ri = const, / = 1. 2, ..., п. (6.5) Согласно (6.2) \ может быть представлена в виде

(6.7)

Отыскивая методом Лагранжа минимум ]x{d[, dl, dl, dl, ... .... dn, dl) при наличии 2ti- 1 условия (6.5) и (6.7), находим следующие условия экстремума:

d(t + /2-iQo/a)

-Х; = 0, i = 2. 3. ..

<3(F--iQu)

dd[ . ddi

(6.8a) ft -1, (6.86) (6.8b)

(6.9a) ft-1, (6.96) (6.9b)

где X, и v, - множители Лагранжа.

Комбинируя соответствующие формулы (6.8) и (6.9) и исключая из них X,, находим

1 a(N,-iQo-iga) 1 d{i ,Q,i-iQ,i)

/ = 2, 3.....ft - 1.

(6.10a) (6.106)

(6.1 Ob)

а условия (6.1) записаны в форме

Qonidn, dn) - Qin-iidn-b dn-i) = 0. Q{)n-i(dn-u dn-\) - Q\n-i{dn-i< dn-2) =

QQ2idl dl) - Qn{d[, d[)=Q.