поглощается количество тепла

(1.3)

i t Н1111 i

если направление тока / противоположно направлению градиента температуры. Величина т носит название коэффициента Томсона. Она зависит от температуры и может быть как положительна, так и отрицательна. Явление Томсона является столь же общим свойством всех проводников электричества, как и предыдущие два эффекта.

Результаты термодинамических теорий термоэлектричества. При замыкании цепи одновременно имеют место

все три рассмотренных выше эффекта (рис. 4). Кроме этого, через термопару проходит тепловой поток от нагревателя к холодильнику, а также выделяется тепло Джоуля. Эти последние эффекты являются необратимыми, что делает невозможным строгий анализ термоэлектричества с позиций классической термодинамики. Вместе с тем, эти эффекты сопровождают каждый термоэлектрический процесс и принципиально неустранимы.

Несмотря на это, первый теоретический анализ рассматриваемых на основе классической термодина-что собственно термоэлектрический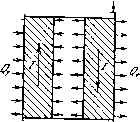

тггтттттш

Рис. 4.

явлений был выполнен мики. Предполагалось, процесс, включающий три обратимых термоэффекта, протекает «независимо» от сопутствующих ему необратимых процессов теплопроводности и джоуль-эффекта.

Первую попытку создать теорию термоэлектричества на этой основе сделал Клаузиус. Однако он пришел к неверным результатам, так как ему не был известен эффект Томсона.

Этот недостаток был ликвидирован Томсоном [1], который сначала теоретически предсказал существование указанного эффекта, а затем и обнаружил его на опыте.

Ход рассуждений Томсона становится очевидным, если рассматривать термопару как обычную тепловую машину,

в которой рабочим агентом является некоторое количество электричества q. Состояние этого агента циклически изменяется по мере прохождения различных участков замкнутой цепи (рис. 5). При этом на контактах между ветвями термопары обратимым образом поглощается теплота Пельтье, а внутри проводников - тепло Томсона. Знак поглощаемого тепла зависит, конечно, от направления тока. Если температуры спаев различны, то алгебраическая сумма теплот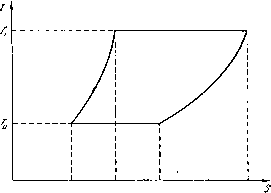

Рис. 5.

отлична от нуля и, в согласии с первым законом термодинамики, равна работе, которую совершает термоэлектродвижущая сила при протекании в цепи данного количества электричества q\

Eq = \l{TOq-~n{T,)q-{-q j (х"- x)dT. (1.4)

Прирост энтропии носителей тока на любом участке процесса легко рассчитывается согласно второму началу термодинамики. В замкнутом цикле этот прирост, очевидно, равен нулю, так что

Из формул (1.6) и (1.1) вытекает первое термоэлектрическое соотношение:

."-.а-Н.. (1.8)

Подставляя его в (1.7), находим также и второе:

11==аТ. (1.9)

Наконец, из этих двух соотношений легко получить еще одно важное равенство:

Z"-Z=:-T-. (1.10)

Как видно из этих формул, все термоэлектрические характеристики: си{Т), П(Г) и х" - - выражаются друг через друга с помощью простых соотношений. Поэтому для экспериментального определения этих величин достаточно измерить хотя бы одну из них. Для этой цели наиболее удобна дифференциальная термо-э.д.с. а (7) благодаря относительной простоте определения ее температурной зависимости.

Соотношения (1.9) и (1.10) подвергались многократной опытной проверке и получили прекрасное экспериментальное подтверждение. Тем не менее, Больцман подверг острой критике теорию Томсона, указав на то, что если джоуле-пым теплом можно пренебречь при малых токах ввиду его

Формулы (1.4) и (1.5) выражают содержание первого и второго начал термодинамики в применении к термоэлектрическому процессу. Они с очевидностью вытекают из диаграммы, изображенной на рис. 5, если учесть, что горизонтальные участки цикла соответствуют протеканию данного количества электричества q через контакты проводников пары, а боковые ветви описывают изменение его состояния по мере продвижения от одного контакта к другому.

Формулы (1.4) и (1.5) тем точнее описывают реальный процесс, чем меньше интервал температур - Tq. В предельном случае {Ту - T - dT) вместо (1.4) и (1.5) находим

dEd-\~{z" - x)dT (1.6)