При р„ <рТ

г т Р°

(4.52)

Формулы (4.51) и (4.52) адекватны формуле (4.49), поэтому выражение (4.50) определяет перепад энтропии при любой температуре воды Гв и окружающей среды Го.с.

Таким образом, эксергия воды определяется по формуле

бв - Тол

\1 о.с

-1-1п

о.сУ

Рп J

(4.53)

При выводе формулы (4.53) было сделано допущение, что изобары в области воды не отклоняются от линии кипения, т. е. не учитывается величина

ев = (кв -кв)- Го.с(sb -sb), (4.54)

связанная с изменением энтальпии и энтропии при уменьшении давления воды до давления насыщенного водяного пара при той же температуре.

Значения начинают заметно отклоняться от значений h

при давлениях, превышающих 230 кПа, а значения - от 5 при

больших давлениях. Таким образом, если вода представляет собой взвешенные в воздухе мелкодисперсные капли с радиусом менее 1 мкм (см. табл. 3.14), то расчёт эксергии воды следует производить по формуле (4.47), прибавляя к ней величину .

Примеры

Пример 4.10. Определить эксергию воды при температуре = 5°С, если температура окружающей среды Го.с = 40°С, а влагосодержание do.c = 0,008 кг вл/кг с.в (р = 100 кПа). Парциальное давление насыщенного водяного пара при температуре воды ts = 5°С определяем по формуле (3.12)

17,504-5

р =0,6112 ехр

= 0,872 кПа.

241,2 + 5;

Парциальное давление водяного пара в воздухе окружающей среды можно определить из выражения (4.13)

р0.с 110-QQQ = 1,397 кПа.

" 0,6221 + 0,008

Удельная теплота парообразования

г = 2500,64 - 2,369 • 5 = 2488,79 кДж/кг . Эксергия воды, согласно (4.63),

ев = 313,15

1,86

278,15 .313,15

+ 2488,79

-1-1п

278,15 313,15 j 1

,278,15 313,15

+ 0,46151п

0,872 1,397

= 249,1 кДж/кг.

4.7.4. Эксергия льда

Эксергия льда определяется по зависимости бл = ААл-Го.сАул»

(4.55)

где ДЛд и - разность энтальпий и энтропии между параметрами льда (Гд, Pjj, /1д и Sj) и параметрами водяного пара в окружающей среде (Г, Ро.с о.с Лй- и 5°<).

На рис. 4.7 в Г-А-диаграмме показана последовательность процессов перехода из одного состояния в другое: фазовый переход - сублимация 1-2, нагрев водяного пара до температуры окружающей среды 2-3 при Гд < Т или охлаждение водяного пара

2-3 при7д>Г„.,. Энтальпия льда

hn~сpTji~fплд • Энтальпия перегретого водяного пара:

- при , > Гд

hn = CpJn-Гпло + суб + Ср(То.с- Тп),

- при Г„., < Гд

Ап = СрТл- rwiQ + г суб ~Ср (Гл - Го.с) •

Поэтому для обоих случаев

А Ал = Ал - Ап = С;,Д7л - Го.с) - Гсуб

(4.56)

Для определения разности энтропии As„ рассмотрим два варианта, когда Гд > Т и при Гд < Т.

««к**************** 4.7. Эксергия влажного воздуха *******************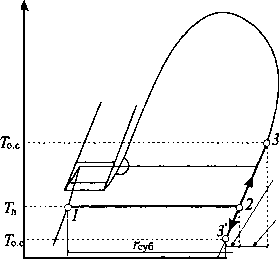

Ср(Тп-То. при Гл>Го.с

Сд(То.с- Tjy) при 7;.с> 7!i

Яп Лп

Рис. 4.7. Соотношение между энтальпиями перегретого водяного пара в окружающей среде и льда

Последовательность процессов при Т„ > Т.с представлена на Г-5-диаграмме на рис. 4.8: фазовый переход - сублимация льда 1-2 (перепад энтропии Гсуб/Гд); изотермическое расширение 2-3 до парциального давления водяных паров в атмосферном воздухе

(перепад энтропии Rln-); изобарное охлаждение 3-4 до тем-

пературы окружающей среды (перепад энтропии минус с п In--).

о.с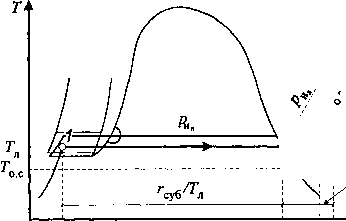

Рис. 4.8. Соотношение между энтропиями перегретого водяного пара

I о с f

в окружающей среде Йц и льда