без штриха и амплитуда индукции обозначена без индекса т), тогда как у нас рмг равно отношению амплитуд (или действующих значений) напряженности магнитного поля и индукции. Это следует иметь в виду при использовании кривых удельных магнитных сопротивлений, приведенных в [3], так как рмл=рмлК2; рмх =

= pmxV 2 и Pmz=pmzK2.

Комплексное сопротивление магнитной цепи с зазорами. Рассмотрим МС рис. 2.7 с зазором, сопротивление которого /?мб значительно меньше сопротивления магиитопровода Zmm- Напомним, что под термином «зазор» в гл. 2 имеется в виду зазор не только немагнитный, но и неэлектропроводящий, например воздушный. Магнитное напряжение (7мб на длине такого зазора находится в фазе с магнитным потоком Ф, поэтому Um6= = /?мвФ и Umr=Um.mr+Umu. Для такой МС на рис. i2.ll, а, в, г к в соответствующих уравнениях следует заменить параметры МЦ,. учитывающие только сопротивление магиитопровода, на их более общие выражения: Rm.m на Rm=Rm.m+Rm6; на Zm=Rm +

+1Хм.м; Um.m на 7м = Ф2м.

Деление комплексного сопротивления на составляющие привело к тому, что при расчете МЦ переменного тока более удобным оказалось оперировать значениями магнитных сопротивлений зазоров, а не проводимостей. Использование последних получило преимущественное распространение при расчете МЦ постоянного тока.

Магнитные системы с соизмеримыми сопротивлениями зазоров и магиитопровода. Потоки рассеяния и выпучивания учитываются.

Имеется в виду МС типа изображенной на рис. 2.4, а. Учитывается сопротивление магиитопровода. Векторная диаграмма показана на рис. 2.12. По действительной оси отложен действующий средний по длине сердечника поток сбор. Большую часть магнитного сопротивления на пути потока рассеяния Фа составляет активное магнитное сопротивление, так как при той длине немагнитного промежутка, которую проходят в пространстве, окружающем магнитопровод, линии индукции потока рассеяния, даже при насыщенном магнитопроводе немагнитный промежуток оказывает сопротивление этому потоку обычно существенно большее, чем магнитопровод. Это означает, что полный поток рассеяния <1),л можно считать совпадающим по фазе с МДС Й и током /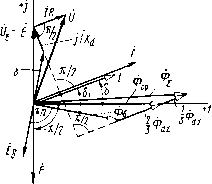

Рис. 2.12. Векторная диаграмма магнитмой системы (с учетом потока рассеяния, сопротивления магиитопровода и зазоров)

обмотки. Поэтому векторы 2Ф1/3 и 6di/3 на рис. 2.12 проведены параллельно вектору тока / обмотки. Для МС с учетом как активного, так и реактивного магнитных сопротивлений МЦ (2.22) и (2.23) могут быть переписаны в векторной форме. Для действующих потоков

Ф,р = Ф,+ 2Ф,/3; Ф, = Ф,р + Ф,/3.

Из векторной диаграммы видно, что рабочий поток Фе отстает от тока обмотки / на угол 6i, а средний поток Фср -на угол 6<6i.

Напряжение О на обмотке МС может быть определено по уравнению U=UE&+jiXd + iR, причем

{yEi + jiXa=UE=-E. (2.44)

Здесь 7Еб=-£б -составляющая напряжения питания, компенсирующая ЭДС £«, индуктированную в обмотке рабочим потоком Фб; d- составляющая напряжения питания, компенсирующая ЭДС, индуктированную в обмотке потоком рассеяния. Разбивка вектора Ое на Ueu ч jtXa принята при изображении векторной диаграммы обмотки со стальным сердечником в курсах теоретических основ электротехники [9]. Индуктивное сопротивление рассеяния Xd=wLd, где приближенно (без учета сопротивления магиитопровода) индуктивность рассеяния Ld = wAdv, причем Adv определяется по (1.20).

В (2.44) и на векторной диаграмме рис. 2.12 [7е -составляющая напряжения питания, компенсирующая ЭДС Ё, наведенную в обмотке средним потоком Фср; ? -напряжение на активном сопротивлении обмотки. Диаграмму электрических напряжений на рис. 2.12 можно дополнить, разложив вектор Ое на составляющие, как это сделано на рис. 2.10, а и 2.11, а.

§ 2.3. Магнитные системы со вторичными обмотками или с электромагнитными экранами

Магнитные системы второго класса (см. табл. 2.2), рассматриваемые в этом параграфе, исследуются упрощенно (предполагается, что вторичные обмотки и электромагнитные экраны не создают потоков, не сцепленных с первичной обмоткой). Ниже рассматриваются представители обеих групп МС второго класса: МС со вторичной короткозамкнутой обмоткой, схватывающей весь поток (группа 1), и МС с КЗВ, сцепленным с частью полного потока (группа II).

Вторичная обмотка охватывает весь поток. Предполагается, что весь поток, созданный первичной обмоткой, сцеплен со вторичной. Учитывается активное сопротивление магиитопровода, зазоров и активное электрическое сопротивление цепи вторичной обмотки.

Для МС второго класса группы I, используемых в ЭМАА, характерны короткозамкнутые вторичные обмотки. Условная электрическая схема такой МС приведена на рис. 2.13, а, на котором активные сопротивления Ri и R2 обмоток и Шг выделены в виде отдельных элементов (вторичная обмотка замкнута на свое собственное активное сопротивление).

Потери в магнитопроводе не учитываются. Нет никаких оснований в начале изучения такой МС утверждать, что МДС первичной и вторичной обмоток направлены встречно (илн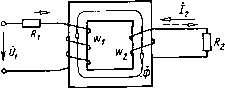

0-CZ1-

(Ь. щк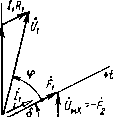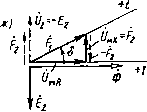

Рис. 2.13. Магнитная система со вторичной обмоткой (сплошные стрелки-согласное, штриховые - встречное направление МДС и Шг)

согласно), поэтому выбор их условно-положительных направлений Делается произвольно. Рассмотрим сначала работу системы при согласных условно-положительных направлениях токов и МДС обмоток W\ и Шг, для которых все величины обозначены на рис. 2.13 сплошными стрелками. Обмотки W\ и связаны между собой общим магнитным потоком Ф. Условно-положительное направление потока Ф тоже можно выбрать произвольно. Для удобства здесь и далее будем связывать его правилом правого винта с током первичной обмотхи.

На рис. 2.13, б, в приведены схемы замещения электрических цепей первичной и вторичной обмоток, а на рис. 2.13, г -схема замещения МЦ. Так как токи в обмотках и поток в магнитопроводе образуют правовинтовую систему, то в первых двух схемах ЭДС Ё\ и £2, индуктированные в ш, и Шг потоком Ф, совпадают по направлению с токами 1] и t2 в этих обмотках; по той же причине в третьей схеме МДС Pi и fj, создаваемые обмотками Wi и Шг, совпадают с потоком Ф МЦ (см. § 2.1).

В отличие от МС рис. 2.7, при изучении которой учитывались потери в магнитопроводе, здесь они ие учитываются, поэтому в схему замещения МЦ (рис. 2.13, г) включено только активное магнитное сопротивление R„ магнитопровода и зазоров (последние на рис. 2.13, а не показаны). Для электрических цепей обмотки Wi (рис. 2.13, б) и Ш2 (рис. 2.13, в) можно написать:

iiRi-Ux=Ei или I\Ri-\-Uei=Ui; и Ei - Ei = ]тОуФ\

Для магнитной цепи (рис. 2.13, г)

(2.45) (2.46) (2.47)

(2.48)

где £, = /,011 и p2=hw2-

По полученным уравнениям на рис. 2.13, д построена векторная диаграмма. По действительной оси отложен поток ф. От потока отстают на 90° обе ЭДС (£i и £2), индуктированные в обмотках. С ЭДС Ё2, наведенной во вторичной обмотке, совпадает по направлению [см. (2.47)] ток /2, а значит, и вторичная МДС £2- Сумма МДС £, и р2 дает магнитное напряжение Омн на активном сопротивлении МЦ [см. (2.48)]. Напряжение Umr совпадает по фазе с потоком Ф [см. (2.48)]. Векторная диаграмма показывает, что между напряжением Uei на индуктивном сопротивлении первичной обмотки и током этой обмотки h угол сдвига фаз меньше 90°. Это означает, что ток первичной цепи имеет не только реактивную, но и активную составляющую. Такую обмотку в эквивалентной схеме замещения нельзя заменить одной ЭДС £i, поэтому на рис. 2.13,6 параллельно £] подключено сопротивление Ri, по которому замыкается активная составляющая первичного тока. Вместо ЭДС Ei на рис. 2.13, 6 можно включить индуктивное сопротивление Хц аналогично тому, как это сделано на рис. 2.9, в (по Хц будет замыкаться реактивная составляющая тока /1). Электрическую цепь первичной обмотки можно заменить и последовательной схемой замещения, аналогичной рис. 2.10, б, в, г. Заменить индуктивностью ЭДС вторичной обмотки, как это следует из (2.46), нельзя.

Разложим вектор МДС первичной обмотки на активную Umr и реактивную Ом х составляющие:

(2.49)

Составляющая Омя находится в фазе с потоком; Окх перпендикулярна потоку. Сравнение (2.48) и (2.49) показывает, что

(2.50)

Замена МДС на магнитное напряжение Ох равносильна замене ее на реактивное магнитное сопротивление вторичной обмотки Лмг, поток в котором отстает от магнитного напряжения на 90°:

(2.51)

Сопротивление Хм2 аналогично индуктивному сопротивлению электрической цепи Х=шЬ, ток в котором отстает от напряжения на 90°. Можно сказать, что комплексное сопротивление Хм2 имеет «индуктивный» характер. Таким образом исследуемая МЦ формально приводится к МЦ с одной обмоткой.

Выразим реактивное магнитное сопротивление вторичной короткозамкнутой обмотки через ее электрическое сопротивление /?2-Учитывая (2.47), получим

/2=и)и;2Ф ?2. (2.52)

Реактивное магнитное сопротивление вторичной обмотки найдем нз (2.51), если подставим в него Ux - Fi [см. (2.50)], которое определим, умножив (2.52) на W2:

м2 = 2«2Ф = »И2/-?2-

(2.53)

На рис. 2.13, а, в, г штриховыми стрелками /2, О2 и F2 показаны условно-положительные направления вторичных тока, напряжения и МДС, если принять положительное направление тока в противоположным рассмотренному выше. При этом в уравнениях (2.47), (2.48) н (2.50) у этих величин изменится знак. Получим: (72 = /2/?2= -£2; Ё1-р2-0„ к; t/w A = f 2-Векторная диаграмма для встречно направленных МДС и W2 изображена на рис. 2.13, ж. Нетрудно видеть, что она отличается от диаграммы рис. 2.13, д только знаками (направлениями) векторов О2 и Р2, что и следовало ожидать.

Покажем, что векторные диаграммы рис. 2.13, д, ж дают физически один и тот же результат, если рассматривать их в совокупности с условно-положительными направлениями величин, показанными на рис. 2.13, а. Для этого рассмотрим момент времени, соответствующий совпадению положительной оси +t (рис. 2.13, д, ж) вращающейся плоскости времени с вектором одной из МДС, например fi. Если бы векторные диаграммы (рис. 2.13, д,ж) были построены для амплитуд, то мгновенные значения всех ве-

личии можно было бы найти в виде проекций амплитуд на эту плоскость времени. Из рис. 2.13, д видно, что при выбранном положении плоскости времени мгновенная МДС первичной обмотки Рц положительна и равна амплитуде МДС первичной обмотки Рщ, а МДС вторичной обмотки Fit отрицательна и равна F2t= = -F2msm6 (f2m -амплитуда МДС вторичной обмотки). Отрицательное значение Fit следует понимать так: предварительно принятое направление /2 (сплошная стрелка /2 на рис. 2.13, а) в этот момент времени противоположно действительному направлению. Таким образом, в действительности ток вторичной обмотки в рассматриваемый момент времени направлен по штриховой стрелке на том же рисунке.

Из рис. 2.13, ж видно, что при выбранном положении плоскости времени (мгновенная МДС Рц положительна и равна Рш) мгновенная МДС вторичной обмотки F2t=F2m sin в и тоже положительна. Последнее следует понимать так: предварительно принятое при построении диаграммы рис. 2.13, ж условно-положительное направление /2 (штриховая стрелка /2 на рис. 2.13, а) совпадает с действительным направлением тока вторичной обмотки. Таким образом, обе векторные диаграммы, несмотря на разные предварительно принятые (условно-положительные) направления МДС в обмотках

и W2, приводят к одинаковым действительным направлениям и одинаковым мгновенным значениям величин Ри и p2t.

Так как при принятых допущениях угол между векторами f i и р2 на рис. 2.13, д всегда больше 90° и меньше 180°, а на рис. 2.13, акт всегда меньше 90° и больше О, то можно сказать, что большую часть времени действительные направления МДС первичной и вторичной обмоток встречны, меньшую часть времени - согласны.

Потери в магнитопроводе учитываются. Идентичность векторных диаграмм МС без потерь в магнитопроводе, но со вторичной обмоткой, замкнутой на активное сопротивление и охватывающей все поперечное сечение магиитопровода (рис. 2.13, д, ж), н векторной диаграммы МС с потерями в магнитопроводе, но без вторичной обмотки (рис. 2.11, а) позволяет сделать следующие выводы:

1) составляющие МДС, магнитного напряжения и тока обмотки, обусловленные потерями в магнитопроводе и вторичной обмотке, имеют одну и ту же фазу (перпендикулярны потоку Ф);

2) суммарное реактивное магнитное сопротивление Хм МЦ в общем случае равно сумме реактивного сопротивления Хм.м, соответствующего потерям в магнитопроводе, и реактивного магнитного сопротивления Хм2 вторичной обмотки;

3) любая из приведенных на рис. 2.11, а или 2.13, д, ж векторных диаграмм может считаться векторной диаграммой МС переменного тока с учетом вторичной обмотки, замкнутой на активное сопротивление и охватывающей все поперечное сечение магиитопровода, потерь в магнитопроводе, активного сопротивления магнито-