разделе будет показано, что на переменном токе при наличии потерь в магнитопроводе поток и МДС не совпадают по фазе).

Магнитные системы с сопротивлением зазоров, значительно большим сопротивления магиитопровода, будем рассматривать с учетом активного сопротивления обмотки. Электрическая цепь МС этой группы эквивалентна цепи с последовательным включением индуктивности (или ЭДС самоиндукции) и активного сопротивления, равного сопротивлению обмотки.

Векторная диаграмма. Магнитная система с зазорами, сопротивление которых значительно больше сопротивления магиитопровода, показана на рис. 2.4, а, на котором активное сопротивление обмотки R в схеме электрической цепи выделено в виде от-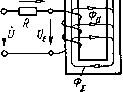

6) 1 О-CZ

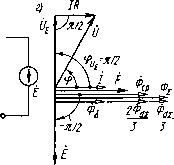Рис. 2.4. Потокораспределение (а), схемы замещения электрической цепн (б н в), векторная диаграмма (г) магнитной системы с большими зазорами

дельного элемента. Схемы замещения ее электрической цепи (рис. 2.4, б, в) отличаются от схем рис. 2.3, б, в только наличием активного сопротивления обмотки. Для рис. 2.4, б, в, по второму закону Кирхгофа, €е = -Ё=]1Х и

(2.15)

При построении векторной диаграммы (рис. 2.4, г) рассматриваемой МС по действительной оси комплексной плоскости отложены совпадающие по фазе действующие комплексные ток /, МДС f = /(0, рабочий поток Фе, потоки рассеяния 2fDdj:/3 и Фй/З, суммарный поток в магнитопроводе Фх. Составляющие напряжения tJ на обмотке МС - это напряжения tls и IR на последовательно соединенных индуктивном X и активном R сопротивлениях. Из прямоугольного треугольника электрических напряжений следует

UE=E=VU-URf. (2.16)

Средний поток в магнитопроводе. На рис. 2.5, а изображена клапанная МС переменного тока, а иа рис. 2.5, б -кривая изменения действующих потоков в сечениях ее сердечника. Кривая

на рис. 2.5, б построена с учетом тех же допущений, какие были приняты при построении кривой рис. 1.3, г. Так как различные витки обмотки МС рис. 2.5, а пронизываются различными по значению потоками, то формулой (2.9), которая была выведена исходя из предположения о том, что все витки обмотки пронизываются одним потоком, мы воспользоваться непосредственно не можем. Однако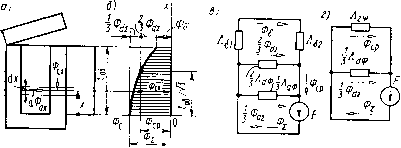

Рис. 2.5. Магнитная система с большими зазорами (а), кривая изменения потоков вдоль ее сердечника (б); схемы замещения магнитной цепи (в н г)

можно считать, что витки обмотки UW, расположенные в слое бесконечно малой толщины йх, пронизываются все одним и тем же потоком Фсж (рис. 2.5, а). Для этих uw витков можно по (2.9) написать: йЕх = (аФо,хйхю, где 6.Ех - ЭДС, наводимая потоком Фсж в витках Aw слоя обмотки толщиной йх; uw = wAxllof,- Полная ЭДС самоиндукции Е может быть определена как сумма ЭДС d£x слоев толщиной йх, на которые разбита вся длина обмотки /об. Так как все витки обмотки соединены согласно и последовательно, то

об об

Величина

(2.17)

(2.18)

называется средним потоком магнитной системы. Ее не следует путать со средним значением синусоидально изменяющегося во времени потока, понятие которого в учебнике не используется. Инте-

грал *cjdjc численно равен заштрихованной горизонтально на

рис. 2.5, б площади, заключенной между кривой изменения потока

вдоль сердечника и осью х. Геометрически Фср - горизонтальная сторона прямоугольника, равновеликого этой площади. Учитывая (2.17) и (2.18), получим

=и)тоФер. (2.19)

При синусоидальном изменении суммарного потокосцепления 4i( = ¥imSin со/, по (2.1) получим е=-d4i(/d/=-w¥imCos со/, откуда

Я„=а)5Г„„ И Е=Ч. (2.20)

Поэтому, учитывая (2.19), можно написать

W = Ф,w. (2.21)

Сравнение (2.21) с (1.29) показывает, что суммарный поток, приведенный по потокосцеплению к числу витков ш, есть не что иное, как средний по длине сердечника поток (Ф1т=Фср).

Рассчитаем значение среднего потока. Подставим (1.11) в (2.18) и проинтегрируем:

= Ф, + 2Ф,,/3.

(2.22)

Суммарный поток в магнитопроводе (у основания сердечника) Ф1=Фв+ Фаг. т. е.

Ф,=Ф,р-ЬФ,/3.

(2.23)

По (1.11) и (2.22) легко показать, что поток в сердечнике Фсх численно становится равным среднему потоку Фср при х=1оъ1У (рис. 2.5,6).

На рис. 2.5, в, г приведены схемы замещения МЦ рис. 2.5, а, составленные с выделением среднего потока. Здесь Aei, Лег, Айф и Ait имеют тот же смысл, что в § 1.2 и на рис. 1.4.

Коэффициенты рассеяния. Коэффициенты рассеяния по потоку и потокосцеплению МЦ переменного тока рассчитываются по тем же формулам, что и на постоянном токе [(см. (1.31) - (1.35)]. Однако поскольку на переменном токе известен обычно средний поток Фср (связанный с напряжением питания), определим отнощение среднего потока Фср к рабочему Фе.

Поток рабочего зазора сцеплен со всеми витками обмотки, поэтому Фб=Чв/ш, где Чв - потокосцепление потока Фе. С учетом (1.34) и (1.29) Фср/ Фб=(Чх/ш)(¥б/ш)=¥1/¥б = а<.г. Таким образом, рабочий поток по среднему можно найти с использованием ко-эффициента рассеяния Ov по потокосцеплению.

Зависимость тока в обмотке от длины зазора. Ток в обмотке МС переменного тока с одним большим рабочим зазором с учетом (1.37) -(1.39)

(2.24)

Уравнением (2.24) не следует пользоваться для практических расчетов, так как оно получено с использованием (1.38), при выводе которого не учитывались потоки выпучивания и рассеяния. Достоинство (2.24) состоит в том, что оно дает связь между током и зазором в явном виде. Эта связь проявляется и в динамике: при включении электромагнита в начальный момент ( рабочий зазор максимален) через его обмотку протекает ток, во много раз больший, чем при притянутом якоре. Электромагнит переменного тока обладает автоматической форсировкой (подробнее об этом см. § 4.1).

Зависимость потока от длины зазора. Из (2.19) и (2.16)

Фер = У2-( ?)2/(и)да).

При больших зазорах это равенство соблюдается достаточно точно; при малых зазорах - приближенно, так как из-за потерь в магнитопроводе и вторичных обмотках векторы IR и Ое не перпендикулярны друг другу (см. ниже в этом параграфе и § 2.3). Уравнение (2.24) показывает, что при уменьшении длины зазора ток / обмотки уменьшается. Это приводит к увеличению среднего потока.

У реальных электромагнитов переменного тока Фср увеличивается при уменьшении зазора от максимального до минимального обычно не более чем на несколько десятков процентов. По сравнению с изменением Фе электромагнита постоянного тока [см. (1.40)] поток Фср электромагнита переменного тока при таком же перемещении якоря изменяется в значительно меньшей степени.

Выше было показано, что

«Фср/Ч-

(2.25)

Так как длина зазора б изменяется в значительно большей степени, чем коэффициент рассеяния и поток Фср (при том же перемещении якоря), то сравнение (2.25) и (1.40) позволяет сделать следующий вывод: рабочий поток МС постоянного тока при уменьшении длины зазора увеличивается в гораздо большей степени, чем у МС переменного тока.

На рис. 2.6 зависимость потока от длины зазора проиллюстрирована кривыми изменения потока вдоль сердечника одной и той же системы при двух крайних положениях якоря (масштабы осей ко-

ординат рис. 2.6, а, б одинаковы). Для этого рисунка можно написать: Ф1б<Ф1ср<Ф2ср=Ф26 = Ф21.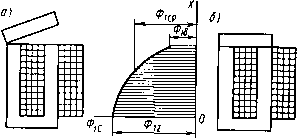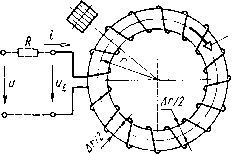

Рис. 2.7. Тороид с равномерной намоткой

Рис. 2.6. Влияние длины зазоров на потокораспределение

Магнитные системы с сопротивлением зазоров, соизмеримым или значительно меньшим сопротивления магиитопровода. Потоки рассеяния и выпучивания не учитываются. Магнитные системы этой

группы рассмотрим на примере тороида с равномерной намоткой (рис. 2.7) сначала без зазоров. Считаем, что весь поток тороида сцеплен со всеми его w витками. Активное сопротивление обмотки R на схеме рис. 2.7 вынесено в виде отдельного элемента. Примем сначала/? = = 0 и u=Ue. в такой МС активные потери в виде теплоты выделяются только в магнитопроводе тороида, на непрерывное перемагничивание которого из сети потребляется активная энергия.

Эквивалентные синусоиды. Как известно [9], при переменном токе мгновенная индукция Bt в ферромагнетике связана с мгновенной напряженностью магнитного поля Я/ в нем динамической петлей гистериса, площадь которой пропорциональна удельным (на единицу массы) потерям в ферромагнетике за один период. Для тороида рис. 2.7 при Аг<г в любом перпендикулярном магнитному потоку сечении тороида

Ф,=В,8, (2.26)

где S - площадь этого сечения. По закону полного тока,

Htl = iw, (2.27)

где Ht - напряженность магнитного поля вдоль средней линии индукции тороида; / - длина последней (/ = 2пг).

Если Аг<г, то приближенно можно считать напряженность магнитного поля Ht и индукцию Bt одинаковыми во всех точках манитопровода тороида. в этом случае динамическая петля гистерезиса для материала магиитопровода при изменении масштабов по осям координат в соответствии с (2.26) и (2.27) будет показывать зависимость потока от тока обмотки тороида (рис. 2.8, а).

Если намагничивание осуществить так, чтобы поток Ф/ в магнитопроводе изменялся синусоидально (по 2.6), что будет иметь место при отсутствии активного сопротивления у обмотки и напря-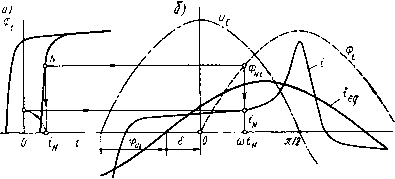

Рис. 2.8. Динамическая петля гистерезиса (а); кривые изменения во времени (б) напряжения ue. потока Ф(, тока i и эквивалентной синусоиды тока ie, при намагничивании ферромагнетика в режиме синусоидального потока

жении источника питания, изменяющемся по (2.8), то ток в обмотке будет несинусоидален (рис. 2.8,6). На рис. 2.8 стрелками показано построение точки in кривой изменения тока по точке Флг/ кривой изменения потока. Масштабы по осям ординат рис. 2.8, а и б для потока, а также по оси абсцисс у рис. 2.8, а и по оси ординат у рис. 2.8, б для тока одинаковы.

Несинусоидальность кривой тока осложняет расчет МЦ, так как применение комплексного метода и построение векторных диаграмм возможно только для величин, гармонически изменяющихся с одинаковой частотой. Для того чтобы сделать все же возможным изучение и расчет МЦ переменного тока комплексным методом, поступают так: заменяют несинусоидальную кривую изменения тока синусоидальной кривой, действие которой до какой-то степени можно считать эквивалентным действию реальной кривой. Основным критерием эквивалентности является равенство активной мощности в цепи с эквивалентной синусоидой тока г