находится под переменным магнитным напряжением, изменяющимся от О до МДС обмотки F, а в схеме замещения рис. 1.4,6 резистор, соответствующий этой проводимости, включен под полное напряжение, равное F, то проводимость этого резистора должна быть равна магнитной проводимости рассеяния ЛdФ, приведенной к МДС обмотки по потоку.

На рис. 1.4, в, г показаны последовательные этапы преобразования исходной схемы замещения рис. 1.4,6 до простейшей цепи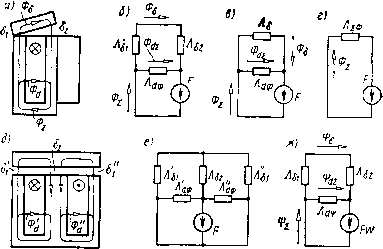

Рис. 1.4. Клапанная магнитная система (а), ее схемы замещения {б, в, г, ж); Ш-образная магнитная система (д) и ее схемы замещения (е, б, в, г, ж)

рис. 1.4, г с источником МДС и суммарной магнитной проводимостью Л1Ф на его зажимах (буква Ф в индексе Лф означает, что в ЛхФ входит проводимость рассеяния, приведенная по потоку).

Легко показать, что суммарная магнитная проводимость всех учитываемых немагнитных промежутков клапанной МС, приведенная по потоку к МДС обмотки,

(1.23)

8 = 5182/(51+82)-

(1.24)

Эту проводимость можно использовать, например, для расчета суммарного потока системы по формуле

Ф5 = Л1Ф, (1.25)

которая соответствует схеме замещения рис. 1.4, г. 26

Поток рабочих зазоров такой системы

Ф, = А,Е. (1.26)

На рис. 1.4, е изображена схема замещения разветвленной Ш-об-разной магнитной системы рис. 1.4,(3 с тремя рабочими зазорами на пути двух рабочих магнитных потоков. На этой схеме Aei, Аб2. Л"б1 - магнитные проводимости зазоров б/, 62 и б/; Ad ф и A"d9 - магнитные проводимости путей потоков рассеяния Фd и ф/, приведенные к МДС обмотки F по потоку. Схему замещения на рис. 1.4, е можно привести к схеме рис. 1.4,6, если считать в ней Лб1 = Аб1+Л"б, и AdФ =Ad9 +A"dt .

Если в схему замещения рис. 1.4, 6, е вместо ЛdФ , ЛdФ и Л"dФ включить Adv, Adw и AW (магнитные проводимости рассеяния, приведенные по потокосцеплению к МДС и числу витков обмотки), а в качестве источника МДС вместо F поставить произведение F на число витков обмотки ш, то по полученным схемам замещения можно будет определить суммарное потокосцепление МС, необходимое, например, для расчета индуктивности обмотки. Такая схема замещения приведена на рис. 1А,ж. Из нее, учитывая (1.24) и (1.22), получим суммарную магнитную проводимость системы, приведенную по потокосцеплению к МДС и числу витков обмотки:

Л5ф=Л5--Л<г=Лг + 2А<,ф/3. (1.27)

Суммарное потокосцепление тогда может быть найдено по формуле

W = AiFw. (1.28)

Уравнение (1.28) можно переписать также в виде

Чг = фу., (1.29)

где суммарный поток, приведенный по потокосцеплению к числу витков обмотки W,

Ф=АР. (1.30)

Подробнее о нем будет сказано в гл. 2.

Коэффициенты рассеяния. Коэффициенты рассеяния по потоку нужны для расчета МЦ с учетом сопротивления магнитопровода методом коэффициентов рассеяния [4]. Максимальный коэ()фици-ент рассеяния по потокосцеплению позволяет определить суммарное потокосцепление МС, а значит - индуктивность обмотки, электромагнитную энергию системы и электромагнитную силу.

Коэффициент рассеяния по потоку офх равен отношению потока Фсх в каком-либо сечении к рабочему потоку Фе:

аф, = Ф,,/Ф5. (1.31)

Так как каждый из потоков можно выразить через произведение магнитной проводимости на МДС обмотки (по упрощенной схеме замещения, не учитывающей сопротивление магнитопрово-

да), то легко получить выражения коэффициентов рассеяния через магнитные проводимости.

Максимальный коэффициент рассеяния по потоку для МС рис. 1.4 с учетом (1.23), (1.25) и (1.26):

аф=Ф,/Ф5 = Л,*/(Л5Л= 1 +AWA5. (1.32)

Коэффициент рассеяния по потоку для любого сечения вертикальных частей магиитопровода той же МС можно получить с помощью (1.31), (1.11), (1.32), (1.12) и (1.26):

Ф.. = (Фе - ФахУ11б)/Ф1 = аФ5 - (AAj) 2 =

Зависимость рабочегопотока от длины зазора. Для МС с одним рабочим зазором справедливо (1.26). С учетом (1.38) получим

= 1 +(Лф/Л5) (1 - = фг - (аф!! - 1) а:2 .

(1.33)

Коэффициент рассеяния по потокосцеплению максимальный:

a = WJW,. (1.34)

По аналогии с (1.32) для рассмотренных МС

очги= l-fAdnr/Aj. (1.35)

Зависимость индуктивности обмотки магнитной системы и рабочего потока от длины зазора. Зависимость индуктивности. По определению [9],

L = JL (1.36)

С индексом t здесь и далее будут обозначаться мгновенные потокосцепление Wt, поток Ф(, индукция Bt, напряженность магнитного поля Hi, МДС Ft. Если обмотки выразить по (1.28), которая справедлива и для Wu и для Ft = iw, и подставить в (1.36), то для индуктивности обмотки МС с зазорами, сопротивление которых значительно больше сопротивления магиитопровода, получим

L=wAj,v. (1.37)

По (1.27) Aiw = Аб-Ь Adw. Для МС с одним рабочим зазором магнитную проводимость Аб зазора можно представить в виде: Аб = = Ат-ьАв, где Ат - магнитная проводимость путей торцового потока; Лв - магнитная проводимость путей потока выпучивания. В явном виде связь индуктивности с длиной рабочего зазора мы получим, если упрощенно будем считать, что А1Ч = Аб и

A,A,=iioS/b, (1.38)

где S - площадь торцов полюсов, образующих рабочий зазор; б-• длина зазора. Тогда

L]iaSw/b. (1.39)

Полученное выражение показывает, что при увеличении зазора 6 индуктивность обмотки МС падает.

(1.40)

Практически рабочий поток зависит от б в меньшей степени, чем по (1.40), из-за влияния потоков выпучивания, сопротивления магиитопровода и других факторов.

Потокораспределение, эпюры магнитного напряжения и потока броневой магнитной системы. Броневая МС (рис. 1.5) состоит из верхнего / и нижнего 6 фланцев, полого цилиндра 3, стопа 4 и якоря 2, обмотки 5. Немагнитная гильза 7 - направляющая якоря 2. Детали 1, 3, 4, 6 жестко скреплены между собой. Вместе с якорем 2 они образуют магнитопровод с пятью зазорами между ними; детали 1,3 и 6- ярмо МС; якорь 2 и стоп 4- сердечники МС. Магнитная цепь броневой МС отличается от ранее рассмотренных тем, , , „

, „ й " Рис. 1.5. Броневая магнитная система

ЧТО ее рабочий зазор

расположен внутри обмотки. Из нерабочих будем учитывать только зазор бг между якорем и верхним фланцем 1. Далее МС будет изображаться в сечении той же плоскостью, в которой показан разрез на рис. 1.5, но без излишней детализации конструкции. Для упрощения примем следующие допущения:

а) поле рассеяния учитывается только на толщине 1„ и /ст, в-пределах которых оно считается плоскопараллельным (картины поля одинаковы в плоскостях, перпендикулярных оси полюсов);

б) потоки выпучивания зазоров 6i и бг в окне магиитопровода отсутствуют (боковая поверхность стопа и якоря занята только полем рассеяния);

в) обмотка имеет равномерную намотку, длина которой /о& равна высоте окна магиитопровода.

В соответствии с допущениями а) и б) потоки в окне магиитопровода на длине 6i не учитываются.

На рис. 1.5 стрелками показаны предварительно принимаемые условно-положительные направления магнитных напряжений: f/„6i - на рабочем зазоре 6i; f/M62 -на зазоре бг; f/Mdin -между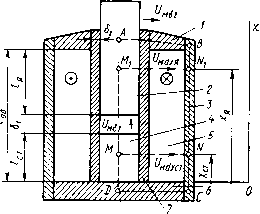

якорем 2 и полым цилиндром 5; (/мйст - между стоном 4 и полым цилиндром 3. За действительное (базовое) направление принимаем направление тока в обмотке МС (крестик и точка). Ось х параллельна оси обмотки и начинается от основания стопа, совпадающего с нижним краем обмотки.

По второму закону Кирхгофа для контура ABCDA: (/мб1 + (Умв2 = =F. Для контура MNCDM получим (1.4): V-ndxcTFxcillob- Уравнение справедливо на всей длине стопа /ст. ПриХст = /ст имеем 11махс1 = об, при ДСст = 0 имеем UudxcrO. Таким образом, на длине стопа магнитное напряжение между стоном и полым цилиндром 3 ярма изменяется линейно от нуля у основания стопа (в начале катушки) до Flctjlou у торца стопа, обращенного к рабочему зазору. На длине стопа потоки рассеяния направлены в сторону предварительно выбранного направления магнитного напряжения.

По второму закону Кирхгофа для контура AMNxBA (обходим контур против часовой стрелки)

м..я=м82-(/о6-я)/о6- (1.41)

Уравнение справедливо на всей длине /я, т. е. при всех Хя, лежащих в диапазоне /ст + б1;дГя/об. Рассмотрим сначала упрощенный случай, когда магнитным сопротивлением зазора 62 можно пренебречь, т. е. (/„62 = 0. Тогда из (1.41)

(»ахя=-(1об-хЖб. (1.42)

Уравнение показывает, что во всем диапазоне изменения Хя, в котором оно справедливо, UMdxH<0, т. е. что потоки рассеяния на

длине якоря направле-(fj X в сторону, противо-

Г1 . п) положную предвари-

тельно выбранному направлению магнитного напряжения.

При Xh=/ct + 6i имеем (/м</хя=-Яя об; при Хч = /об имеем UyidxR = =0.

На рис. 1.6, а показано потокораспределение броневой МС, построенное в соответствии с эпюрой изменения магнитных напряжений, изображенной на рис. 1.6, б по (1.4) на длине стопа и по (1.42) на длине якоря. Напомним, что магнитное напряжение на сопротивлении принимается совпадающим с потоком в этом сопротивлени. Отличие в направлении иахя между точками Ml и Л1 на рис. 1.5 и потока Фй„ на рис. 1.6 не противо-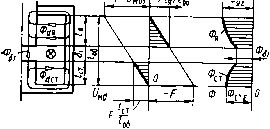

Рис. 1.6. Броневая магнитная система с одним зазором:

а - схема потокораспределения; б - эпюра изменения магнитного напряжения на проводимости рассеяния- в - кривая изменения потоков в сечениях сердечников

речит этому правилу потому, что стрелка (/мйхя иа рис. 1.5 обозначает условно-положительное направление напряжения (и потока), а стрелка Odn на рис. 1.6, а - действительное направление потока (и напряжения), которое на этом участке оказалось противоположным условно-положительному.

На рис. 1.6,0 приведена эпюра изменения потока в сечениях якоря и стопа. Рис. 1.6, а, в показывает, что броневая МС имеет два максимума потока: Фях -в том сечении якоря, которое совпадает с верхним краем обмотки (при зазоре 62 = 0), и Фстх - в сечения стопа, совпадающем с нижним краем обмотки. Фя1 = Фб1----Ф<гя1; Фстх = Фб14-Ф<гст1.

При 62=0 и (/мв20 потокораспределение броневой МС сложнее. Формула (1.41) показывает, что при Хя = /об имеем /Умй1я = = (/мб2, а при л:я = /ст + б1 = /об-/я имеем

Uux. = U,,~FlJl. (1.43)

Для (/мб2< я об потокораспределение и эпюры изменения магнитных напряжений и потоков показаны на рис. 1.7, а, б, в, а для Ь.мв2>/я об - на рис. 1.7, г, д, е. Последний случай представляет меньший интерес, так как характерен для малых длин рабочего-зазора 6], при которых магнитные проводимости зазоров 6] и 62 значительно больше проводимости рассеяния и последней можно пренебречь.

При большой и средней длине рабочего зазора 61 при Хя = /об-/я обычно имеет место неравенство (/мб2< я об. Так как в этом случае при Хя = 1об получается t/MdxH=/Умб2>0. а при Xh = /o6-/я напряжение (/м(;хя<0, то можно показать, что при некотором Хя = /об.р = = lo6-Ui62loc</F магнитное напряжение (Умйхя = 0 (/об.р-расчетная длина обмотки). Через эту координату дГя = /об.р на рис. 1.7,а,б,в проведена горизонтальная штриховая линия. Ниже этой линии потоки рассеяния Фйя (рис. 1.7, а) направлены в сторону, противоположную предварительно выбранному направлению Uudxa (рис. 1.5), выше-потоки рассеяния Ф"с(я (рис. 1.7, а) направлены в сторону, совпадающую с предварительно выбранным направлением ихя.

Проследим по рис. 1.7, а, в изменение потоков в сечениях сердечников. У основания стопа поток равен Фоп; по мере приближения к рабочему зазору в сечениях стопа поток уменьшается, так как от него ответвляются потоки рассеяния OdcT на длине стопа /сг (на рис. 1.7,0 условно показана одна линия индукции замкнутого контура этого потока). Поток в верхнем торце стопа при принятых Допуще1шях равен потоку в нижнем торце якоря (Фб1 на-рис. 1.7,0, 0).

На длине якоря от нижнего торца до нейтрального сечения (расчетная длина якоря /я.р на рис. 1.7, о) поток в сечениях якоря >величивается от Фб1 в торце до Фях (рис. 1.7,0) в нейтральном течении за счет добавляющихся к рабочему потоку Фб1 потоков рассеяния Фя (рис. 1.7, о). В нейтральном сечении суммарный по-