в остальных случаях левитацию можно осуществить только в динамических системах, например в индукционных опорах, в которых переменное магнитное поле воздействует на токи, индуктируемые в объекте левитации. Чаще всего, однако, не требуется обеспечивать левитацию объекта, поэтому во многих случаях магнитные опоры используются для восприятия нагрузки только в одном направлении или в одной плоскости.

§ 15.1. Опоры на постоянных магнитах

Поясним смысл исследований Ирищоу и Браунбека на примере взаимодействия двух постоянных магнитов (ПМ) 1 и 2 (рис. 15.1,а,б). Пусть ПМ расположены относительно друг друга разноименными полюсами и один из них (ПМ /) закреплен (рис. 15.1,а). При у=0 и z=0 на ПМ 2 в противоположных направлениях будут действовать гравитационная сила Рг и электромагнитная сила Рэм* притяжения к ПМ /. Предположим,

Рзнх.Рг

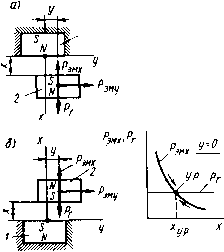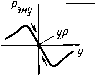xconst

MP у

Рис. 15.1. Иллюстрация иевозможиости осуществить левитацию иа основе взаимодействия постоянных магнитов

что При некотором расстоянии jCh.p эти силы компенсируют друг друга. Однако малейщее смещение ПМ 2 вверх приводит к его дальнейшему движению в этом направлении без приложения внещ-ней силы, а смещение вниз - к его падению. Таким образом, равновесие рассмотренной системы в вертикальном направлении неустойчиво. При горизонтальном смещении ПМ2, например по оси у при 2=0 и A;=const, как показано на рис. 15.1, а, возникает электромагнитная сила (в данном случае сила Рэму), возвращающая

N S ШШ

N S

Рис. 15.2. Комбинированная опора с использованием постоянных магнитов и механических подшипников

ПМ2 в центральное положение. Следовательно, в горизонтальной плоскости равновесие системы устойчиво. Так как в одном из направлений устойчивое равновесие не реализуется, то левитацию ПМ 2 обеспечить невозможно.

К последнему выводу мы также придем, если рассмотрим два ПМ при расположении их друг к другу одноименными полюсами и закрепленном нижнем ПМ (рис. 15.1, б). Отличие заключается только в том, что в этом случае в вертикальном направлении можно обеспечить устойчивое равновесие, а в горизонтальном нельзя.

Несмотря на то что левитацию на ПМ обеспечить нельзя, опоры с ПМ широко используются совместно с другими видами опор (механическими, диамагнитными и др.) Примером может служить комбинированная опора (рис. 15.2), в которой роль упорного подшипника выполняет один укрепленный на валу 4

кольцевой ПМ 2 совместно с двумя фиксированными кольцевыми ПМ ] и 3. Постоянные магниты обеспечивают стабилизацию вала в горизонтальной плоскости. Стабилизацию в радиальной плоскости осуществляют механические подшипники 5 и 6.

§ 15.2. Индукционные и диамагнитные опоры

Индукционные опоры. Принцип их действия основан на стремлении неферромагнитного электропроводящего тела, помещенного в неоднородное переменное магнитное поле, перемещаться в направлении уменьшения напряженности поля, что приводит к снижению вихревых токов в теле и соответственно- к снижению потерь в системе. Чем больше напряженность {или индукция) поля и их градиент, тем больше «выталкивающая» электродинамическая сила Кд. При нулевых значениях напряженности (индукции) или их градиента сила отсутствует.

Рассмотрим систему (рис. 15.3, а) из двух (/ и 2) коаксиальных, но не копланарных витков, по которым протекают равные по амплитуде, но противоположные по фазе синусоидальные токи. На рис. 15.3, а показаны линии магнитной индукции поля, в том числе (более толстыми линиями) сепаратрисы. На рис. 15.3,6, в приведены графики распределения составляющих магнитной индукции и электродинамической силы соответственно по осям у и системы (рис. 15.3,а).

Представим себе сначала, что мы имеем невесомое неферромагнитное электропроводящее тело 3, которое поместим в нашу сис-

тему между точками Б и Б по оси х или между точками Г и Г по оси у (рис. 15.3,а). Тогда на это тело будет действовать соответственно либо сила Рэдх, либо сила Рэжу, стремящиеся переместить его в особую точку А, в которой магнитная индукция равна нулю. Таким образом для невесомого тела точка А является точкой устой-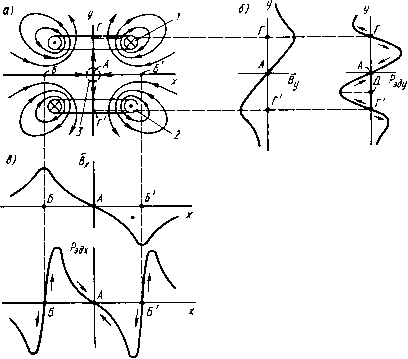

Рис. 15.3. Иллюстрация возможности реализовать левитацию в индукционной системе

чивого равновесия. Из рис. 15.3 следует, что в точках Б, Б, Г, F электродинамическая сила равна нулю, но эти точки являются точками неустойчивого равновесия.

Теперь рассмотрим реальный случай - на тело 3 действует сила веса. Поместим это тело в точку А (рис. 15.3, а). Так как в этой точке сила Рэд равна нулю, то тело опустится. При этом могут быть два варианта: либо на участке А-Д (рис. 15.3,6) возрастающая сила Рэду уравновесит силу веса (тогда наступит левитация тела), либо тело «проскочит» точку Г и будет падать дальше.

На рис. 15.4 показана еще одна индукционная опора. Она состоит из замкнутого трехстержневого магнитопровода /, обмотки переменного тока 3 и электропроводящего неферромагнитного диска 2. При протекании тока по обмотке 3 на диск 2 действует электродинамическая сила, направленная в сторону снижения потокосцепления обмотки с диском, т. е. вверх. Такая система более экономична, так как в ней улучшена электромагнитная связь источ-

ника поля и электропроводящего тела благодаря применению магнитопровода. Однако левитация в такой системе не реализуется, так как устойчивое равновесие диска возможно только на вертикальной оси. Смещение диска по горизонтальной оси ограничивается центральным стержнем магнитопровода.

Диамагнитные опоры. Так как у диамагнетиков Цг<1, го они выталкиваются из магнитного поля. Сила, действующая на единицу объема «пробного тела» (см. § 9.2) из диа-магнетика, равна

/K = N(l*r-l)grad 2]/2, (15.1)

где Я -напряженность магнитного поля.

При полной компенсации веса тела силой выталкивания из поля имеем равенство

1*0(!х,- indHmJ2=pg, (15.2)

Рис. 15.4. Индукционная опора с замкнутым магнитопроводом

где рд - плотность материала диамагнетика; - ускорение свободного падения; г/ -вертикальная ось системы координат.

Отсюда определяется градиент квадрата напряженности магнитного поля, необходимый для подвешивания диамагнитного тела.

У тел, которые ведут себя как диамагнетики при нормальных температурах, р., мало отличается от единицы, поэтому значения {дН/ду)т1п для них велики: для висмута - (-9,5-10 А/м»), для пиролитического графита - (-0,62-10» А/м). Создать такую неоднородность поля непросто, особенно для первого материала, поэтому такого вида опоры используют в технике в основном совместно с другими опорами (чаще всего на постоянных магнитах).

Предпочтительны в этом отношении идеальные диамагнетики (1г = 0)-сверхпроводники, находящиеся в состоянии сверхпроводимости.

Рассмотрим систему из двух разных по диаметру коаксиальных, но не копланарных обмоток с разнонаправленными постоянными токами рис. 15.5, а, причем МДС верхней обмотки меньше, чем МДС нижней обмотки. Картина магнитного поля такой системы отличается от картины поля системы, изображенной на рис. 15.3, а: особая точка А смещена по оси у вверх от оси х; под, осью х на оси у имеется вторая особая точка - точка Б. Если поместить сверхпроводящую сферу 3 с ц = 0, как показано на рис. 15.5,6, то линии магнитной индукции будут ее огибать. На сферу по оси будет действовать сила в направлении точки А. Проведя анализ, аналогичный анализу системы, изображенной на рис. 15.3, а, можно показать, что и в данном случае обеспечивается левитация.

Удельная сила, действующая со стороны магнитного поля на единицу плоской поверхности идеального диамагнетика,

A=fi2/2ix„, (15.3)

где В - магнитная индукция у поверхности диамагнетика.

при В = 0,1 Тл имеем /s«4-103 Н/м (или -40 гс/см), т. е. сила мала. Для ее увеличения необходимо повышать индукцию, а соответствеийо и напряженность магнитного поля. Однако, как известно, сверхпроводники теряют свои сверхпроводяшие свойства при критической напряженности магнитного поля -Якр, значение которой зависит от материала и температуры. При абсолютном ну-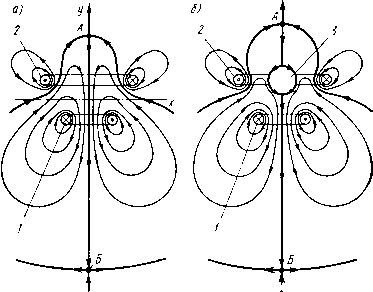

Рис. 15.5. Иллюстрация возможности осуществления левитации диамагнитного тела

ле Якр, например для массивного свинцового образца (сверхпроводник первого рода), составляет 6,4-10 А/м, что для воздуха соответствует магнитной индукции всего 0,08 Тл.

При Якр сверхпроводники первого рода теряют и свойства идеального диэлектрика.

Ограничением использования сверхпроводников первого рода для опор являются также очень низкие температуры, при которых эти материалы приобретают сверхпроводимость (обычно несколько Кельвинов при нулевой напряженности магнитного поля; если же материал находится в магнитном поле, то критическая температура снижается). Это требует громоздких и дорогих криогенных установок на основе жидкого гелия.

В последнее время достигнуты большие успехи в получении ряда новых металлокерамических сверхпроводников с относительно «теплой» сверхпроводимостью (при температуре выше температуры сжижения азота). Критическая напряженность магнитного поля, при которой эти материалы переходят в нормальное состояние,

достигает 7,97-10 кА/м (соответствующая магнитная индукция в воздухе 100 Тл). Следует, однако, отметить, что эти материалы относятся к сверхпроводникам второго рода (иногда из последних выделяют сверхпроводники третьего рода, обладающие магнитным гистерезисом), которые в отличие от сверхпроводников первого рода имеют не два, а три состояния - нормальное, смешанное и сверхпроводящее. В смешанном состоянии их электрическое сопротивление несоизмеримо меньше, чем в нормальном состоянии, но в отличие от сверхпроводящего состояния магнитный поток проникает в материал. Эффект Мейсснера в этих материалах проявляется в ограниченном интервале напряженности поля, далеко не достигающем напряженности Якр.

§ 15.3. Кондукционные,

магнитогидродинамические

и магнитоферрожидкостные опоры

Кондукционные опоры. Функционирование этих опор основано на магнитоэлектрическом принципе действия: используется сила, действующая на проводник с током, расположенный в магнитном поле. Эти опоры позволяют развить высокую подъемную силу. Проводник с током может быть твердым или жидким. В последнем случае опоры называются магнитогидроди-намическими (МГД) кондукционного типа. Существуют также МГД-опоры индукционного типа, в которых ток к жидкости не подводится извне, а наводится от магнитной системы. Магнитогидродинамические опоры индукционного типа по сравнению с МГД-опорами кондукционного типа не требуют токоподводов к жидкости. Это имеет большое значение, так как во многих случаях в МГД-опорах кондукционного типа необходимо создавать скользящие контакты, что представляет серьезную трудность, особенно при подводе к проводнику больших токов. Однако МГД-опоры индукционного типа менее эффективны по затрате энергии на единицу развиваемой ими силы.

Рис. 15.6 иллюстрирует принцип действия МГД-опоры кондукционного типа. Между перемещающейся со скоростью V пластиной 5 и неподвижной опорой 2, выполненных из неэлектропроводящего материала, находится электропроводящая жидкость 4, через которую пропускается ток i, подводимый к ней через электроды 1 и 3. Поперечно к направлению тока создается магнитное поле с индукцией В. В результате возникает электродинамическая сила Рэд, стремящаяся совместно с силой гидродинамического подпора, обусловленного относительным движением поверхностей, поднять пластину 5. В отличие от гидродинамических опор в МГД-опоре обеспечивается возможность подъема тела при отсутствии относительного перемещения.