При промежуточных положениях якоря, при которых магнитные сопротивления зазоров и магиитопровода соизмеримы друг с другом, необходимо учитывать все факторы: сопротивление магиитопровода, зазоров (с учетом выпучивания) и поток рассеяния.

В соответствии с вышесказанным МЦ ЭМАА можно разбить на три группы (табл. 1.1). В § 1.2 учебника описаны расчеты МЦ I группы; МЦ II и III групп рассмотрены в [1-8].

§ 1.2. Магнитные цепи с сопротивлением звзоров, знвчительно большим сопротивления мвгнитопроводв

При рассмотрении МЦ этой группы сопротивление магиитопровода не учитываем.

Расчет магнитного напряження на проводимости рассеяния. Определим с помощью второго закона Кирхгофа значение и направление магнитного напряжения иш (рис. 1.2, а) между любой точкой М на левой вертикальной части магиитопровода и точкой N на его правой части. Считаем заданными размеры МС, а также значение и направление (действительное) тока в обмотке (крестик и точка в кружках). Предварительно выбранное условно-положительное направление Umcix показано на рис. 1.2, а стрелкой (от М к N). Для контура MNCDM по (1.3) можно написать Uudx=SxF/ /5об, где Sx-площадь части поперечного сечения обмотки, охваченной контуром обхода MNCDM; /" - МДС обмотки; 5об -площадь поперечного сечения обмотки, расположенного внутри контура ABCDA; /"/5об - плотность МДС (принимается одинаковой во всех точках поперечного сечения обмотки).

Будем считать, что оба поперечных сечения обмотки имеют форму прямоугольника со сторонами с и /об, перпендикулярными и параллельными вертикальным и горизонтальным частям магиитопровода, и что точки Af и Л находятся на одинаковом расстоянии x от нижней горизонтальной границы поперечного сечения обмотки. Тогда при ширине поперечного сечения обмотки с получим Sx = xc;

5об = /обС и

Предположим, как это обычно делается при расчетах МЦ, что поле рассеяния рассматриваемой системы плоскопараллельно в пределах толщины слоя, равного на рис. 1.2 длине /об обмотки.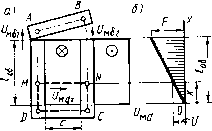

Рис. 1.2. Магнитная система с распреде-ленно"? МДС

Тогда можно утверждать, что линии индукции поля рассеяния, лежащие в плоскости, проходящей через точки М и /V и показанные л сечении А-А рис. 1.1,6, все находятся под магнитным напряжением, определяемым (1.4).

На рис. 1.2,6 построена эпюра изменения этого напряжения. При всех названных выше допущениях ее можно считать эпюрой изменения магнитного напряжения на воздушном промежутке, в котором замыкаются линии индукции потоков рассеяния (кратко «магнитное напряжение на проводимости рассеяния»).

Покажем, что полученный результат не зависит от выбранного контура обхода. По второму закону Кирхгофа для контура ABNMA (рис. 1.2, а) UM6i + UM62-UMdx = F(lo6-x)/lo6. Внутри контура оказалась часть поперечного сечения обмотки, пропорциональная длине /об-X. Магнитное напряжение Умах для этого контура в уравнение вошло с минусом, так как оказалось направленным навстречу обходу его по часовой стрелке. Так как f/M6i + мб2 = -/ (по второму закону Кирхгофа для контура обхода ABCDA), то уравнение для контура ABNMA принимает вид: F-Udx = Flo6/lo6-xF/lo6-Окончательно получаем (1.4).

Магнитные цепи, в которых магнитное напряжение на проводимости рассеяния изменяется линейно от нуля до МДС обмотки, как МЦ на рис. 1.2, называются магнитными цепями с распределенной магнитодвижущей силой; МЦ, в которых магнитное напряжение на проводимости рассеяния не изменяется и равно МДС обмотки, называются магнитными цепями с сосредоточенной магнитодвижущей силой. Большинство ЭМАА относятся к цепям с распределенной МДС. В гл. 1 и 2 при изучении МЦ, сопротивление зазоров которых значительно больше сопротивления магиитопровода, будем иметь в виду только такие МЦ.

Изменение потока вдоль сердечника магнитной системы с распределенной МДС. Ниже приводится вывод формул, сделанный для МС рис. 1.3, а при следующих допущениях:

а) поле рассеяния в пространстве, окружающем магнитопровод, принимается плоскопараллельным (в плоскостях, перпендикулярных оси обмотки, картины поля одинаковы и имеют вид поля, близкого к изображенному в сечении А-А на рис. 1.1,6); толщина плоскопараллельного поля рассеяния U равна длине обмотки /об (рис. 1.3, а), вне этой толщины поле рассеяния отсутствует;

б) потоки выпучивания зазоров замыкаются между якорем и участками длиной /с-/об вертикальных частей магиитопровода;

в) обмотка имеет равномерную намотку.

При расчетах МС правильнее магнитные проводимости рабочих зазоров б] и бг рассчитывать с учетом действительной области, занимаемой потоками выпучивания. Тогда для толщины плоскопарал--ельного поля рассеяния U остается не занятая потоком выпучивания длина сердечника, в общем случае не равная длине обмотки Об. Полученные ниже формулы, как правило, приближенно при-

годны и для иф1о5- о делении магнитного поля на области выпучивания и рассеяния см. [3].

На рис. 1.3, а показана схема потокораспределения рассматриваемой МС, соответствующая принятым допущениям. Поток рассеяния Odx слоя плоскопараллельного поля рассеяния толщиной /об-X условно обозначен одной линией индукции и фигурной скобкой, высота которой равна толщине этого слоя. На рис. 1.3, а видно, что этот поток пронизывает поперечные сечения pq и тп маг-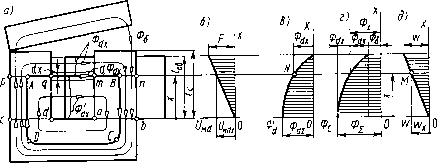

Рис. 1.3. Схема потокораспределения (а) и эпюры изменения:

б - магнитного напряжения на проводимости рассеяния; в-потока рассеяния Ф, добавляющегося к потоку на длине об * -потока Ф, проходящего через сечения сердечника; д - числа витков, охваченных контуром ABCDA

нитопровода. Поток рассеяния Фdx. слоя плоскопараллельного поля рассеяния толщиной х условно показан также одной линией индукции и фигурной скобкой, высота которой равна толщине этого слоя. На рис. 1.3, а видно, что Фdx не пронизывает поперечные сечения pq и тп магнитопровода. Сказанное можно записать в виде следующих уравнений:

Фсх=Ф8 + Фл=Ф£-Ф; Ф!:=Ф5-ЬФ45; %=ах + ах, (1.5) где Фс;с -поток в сечении сердечника с абсциссой х; Фе -рабочий поток МС; Фг - суммарный поток МС, проходящий через сечения cd и аЬ магнитопровода; Фх - суммарный поток рассеяния.

Мысленно представим себе плоскопараллельное поле рассеяния МС на рис, 1.3, а толщиной 1оь-х состоящим, как слоеный пирог, из большого количества слоев толщиной йх. Каждый такой слой несет в себе бесконечно малый поток рассеяния йФdx. Если сложить потоки этих бесконечно узких слоев на толщине /об-х, то получим поток рассеяния, который проходит через сечения pq и тп магнитопровода:

(1.6)

Ф,= I (1Ф

По закону Ома для участка МЦ

dФ.-м</xdЛ4. (1-7)

где (/мйдг - магнитное напряжение, под которым находятся линии лндукции слоя плоскопараллельного поля рассеяния толщиной dx в немагнитном промежутке между вертикальными частями магнитопровода (рис. 1.3,6); dAd - магнитная проводимость этого слоя (d перед Ad - знак дифференциала, индекс d показывает, что речь идет о потоках рассеяния).

Как для любого плоскопараллельного поля,

йАа=йКАх, (1.8)

где/id- удельная проводимость, соответствующая картине поля в сечении А-А рис. 1.1,6. Расчет Ad описан в [3, 4].

Для МС с распределенной МДС справедливо (1.4). Подставим <1.7), (1.8) и (1.4) в (1.6) и проведем интегрирование:

l,I-xux=±-,\,UF (l-) . (1-9)

При х=0 поток Фdx превращается в суммарный поток рассеяния:

Ф.==!оУоб/2.

(1.10)

С учетом (1.5), (1.9) и (1.10) окончательно поток в любом сечении сердечника и ярма с координатой х равен:

Фс= Фг + Фаъ - %jixyili = Ф - ФахУ11б.

(1.11)

Кривые изменения потоков Фd и Фс построены на рис. 1.3, в, г.

Приведение магнитной проводимости рассеяния по потоку и по-токосцепленню. «Приведение» делается для удобства расчета потока и потокосцепления рассеяния МС с распределенной МДС. Под магнитной проводимостью рассеяния Лйф, приведенной по потоку к МДС обмотки, подразумевается такая проводимость, которая, будучи умноженной на МДС обмотки, даст поток рассеяния. Аналогично, под проводимостью рассеяния Adv, приведенной по пото-косцеплению к МДС и числу витков обмотки, подразумевается такая проводимость, которая, будучи умноженной на МДС и число витков обмотки, даст потокосцепление рассеяния. Приведенная по потокосцеплению проводимость рассеяния необходима также для определения индуктивности рассеяния и электромагнитной энер-1ии, запасенной в поле рассеяния. При расчете составляющей силы, обусловленной изменением поля рассеяния, в энергетическую формулу необходимо подставлять проводимость рассеяния, приведен-"УЮ по потокосцеплению. В гл. 2 будет показано, что при расчете

мс переменного тока используется главным образом тоже приведение по потокосцеплению.

Приведение по потоку. Суммарный поток рассеяния можно представить в виде произведения МДС F на некоторую магнитную проводимость, которая учитывает не только размеры системы, но и изменение магнитного напряжения:

Ф,, = Л,ф/-. (1.12)

Эта проводимость (Лф) называется магнитной проводимостью рассеяния, приведенной по потоку к МДС обмотки.

Суммарная магнитная проводимость плоскопараллельного поля рассеяния рассматриваемой системы, определяемая только ее геометрией, не учитывающая распределение МДС вдоль сердечника и соответствующая суммарному потоку рассеяния Фг, равна

(1.13)

Принимая во внимание (1.10), (1.12) и (1.13), можно написать Лйф=АфЛ„ (1-14)

гле кф =\/2 -коэффициент приведения по потоку проводимости рассеяния МС с распределенной МДС к МДС обмотки. Приведением по потоку следует пользоваться при расчете потоков.

Приведениепо потокосцеплению. По аналогии с (1.6) суммарное потокосцепление рассеяния

(1.15)

где d4dx -потокосцепление потока рассеяния йФс1х слоя плоскопараллельного поля рассеяния толщиной dx. Поток с1Ф<л сцеплен только с той частью витков Шх обмотки, которая охватывается контуром ABCDA этого потока. Если полное число витков обмотки w, то

(1.16)

Эпюра изменения числа витков обмотки, сцепленных с потоками рассеяния, приведена на рис. 1.3,(3. Эту эпюру следует понимать так. Ордината Шх точки М эпюры, имеющей абсциссу х, означает то число витков, с которым сцеплен поток йФах бесконечно тонкого слоя плоскопараллельного поля рассеяния магнитной системы, отстоящего от нижнего края обмотки на расстоянии х.

Потокосцепление йах потока йФах равно произведению этого потока на число витков Wx, с которым он сцеплен:

(1.17)

Подставим (1.7), (1.8), (1.4) и (1.16) в (1.17); подставим также {\.\7) в (1.15) и проведем интегрирование

J об «об

(1.18)

Для расчета суммарное потокосцепление рассеяния удобно представить в виде произведения некоторой магнитной проводимости рассеяния Ла> на МДС F и число витков w обмотки. Проводимость Ad-v учитывает как изменение магнитного напряжения на проводимости потоков рассеяния, так и изменение числа витков, с которым сцеплены потоки рассеяния. Суммарное потокосцепление рассеяния

Wa = A.Fw, (1.19)

где под Adv имеется в виду

Ad4r=A4-Ajij- (1-20)

Проводимость Adv называется магнитной проводимостью рассеяния, приведенной по потокосцеплению к МДС F и числу витков w обмотки; к - коэффициент приведения проводимости рассеяния по потокосцеплению к МДС F и числу витков w; Adi - по (1.13).

Сравнение (1.18) с (1.19), (1.20) и учет (1.13) показывают, что магнитная проводимость рассеяния, приведенная по потокосцеплению,

ЛФ = А,/3 (1.21)

и что коэффициент приведения по потокосцеплению =1/3. Заметим здесь, что по (1.21) и (1.14)

Ач==2Айф/3. (1.22)

Схемы замещения магнитных цепей. Суммарная магнитная проводимость. По аналогии со схемами замещения электрических цепей можно составлять схемы замещения МЦ. Это облегчает их расчет и систематизирует наши представления о принимаемых при этом расчете допущениях.

На рис. 1.4,0 показана клапанная МС, а на рис. 1.4, б-схема замещения ее МЦ, составленная без учета сопротивления магиитопровода. Каждому немагнитному промежутку МЦ соответствует резистор электрической цепи (буквами Аеь Аег и AdФ обозначены проводимости этих резисторов). В схеме замещения МДС выпол-5*ет функцию, аналогичную функции ЭДС электрической схемы. 0 схеме замещения рис. 1.4, б можно рассчитать поток Фе в рабо-их зазорах 6i и бг, суммарный поток рассеяния Фdз: и суммарный оток ф,. при заданной МДС обмотки F и заданных размерах сис-емы, позволяющих рассчитать магнитные проводимости Аеь Лб.> \\Я1 ("Роводимость Ad» - по (1.14) и (1.13); Aei и Авг -по * oj). Так как магнитная проводимость рассеяния исходной МЦ