При этом

4„ = JjB(x, y)w(x, y)(iS.

где S - площадь обмотки; В{х, «/)-переменное значение индукции; w(x, i/) - переменное значение числа витков обмотки, пронизываемых элементарным потоком.

Определим для наиболее простого случая (рис. П.25) при следующих допущениях: магнитное поле между полюсами принимаем однородным, а вторичные катушки считаем бесконечно тонкими. Тогда

„ = i + n=iB,S,-B,Sn). Здесь и Yii - потокосцепление левой и правой катушек; Ша - число витков катушки; Sj и Su - площади левой и правой катушек, находящихся в магнитном поле (рис. П.26).

На рис. 11.26, а изображено расположение сигнальных катушек относительно полюсов магнитной системы при смещении их

а/2+х а/2-х

В) Ut,„ jj

Рис. 11.26. Расположение обмотки трансформаторного преобразователя в зазоре магнитопровода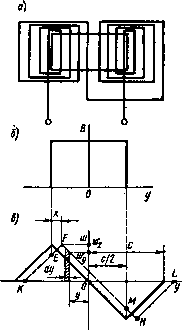

Рис. 11.27. Распределение вторичных витков в зазоре магнитопровода

иа расстояние х. Последовательное и встречное включение сигнальных катушек отражено иа рис. 11.26,6. Учитывая, что Si = &(a/2-f--{х) и Si,= {al2-x)b, где л: - перемещение вторичной обмотки, а и b - размеры полюса, получаем

(11.6)

Подставляя (11.6) в (11.5), находим и =fЪ>Bwфx.

Выходной сигнал при принятых допущениях линейно зависит от перемещения вторичной обмотки.

Рассмотрим теперь процесс образования выходного сигнала преобразователя при распределенных вторичных катушках (рис. 11.27,а). Будем учитывать только магнитное поле между полюсами, а распределение витков считать равномерным. Число витков вторичной обмотки, пронизываемых элементарным потоком с учетом встречного включения катушек, изображено ломаной сплошной линией на рис. 11.27, в для симметричного положения обмотки. При смещении обмотки распределение витков происходит по линии KFMHL.

Элемеитариое потокосцепление на расстоянии у от начала координат (рис. 11.27, в).

d№y=WyйФy. (11.7)

При этом Wy - число витков вторичной катушки, соответствующее координате у, dQj, -элемеитариое значение потока, пронизывающего элементарную площадку dS вторичной катушки;

йФуВйЗ; dS=buy. (11.8)

Здесь Be -магнитная индукция в воздушном зазоре; 6 -размер полюса. Из уравнений (11.7), (11.8) получаем

dy=B,Wybdy. (11.9)

Зависимость w{y) имеет изломы (рис. 11.27,в), поэтому разобьем ось у на ряд участков, где эта зависимость выражается прямой линией без изломов. Участки КЕ и MHL ие рассматриваются, так как они ие создают потокосцепления. Выразим зависимость w{y) для каждого из участков.

Для первого участка зависимость w[y) можно определить из уравнения прямой, проходящей через две заданные точки К с координатами (-а-\-х и 0) и F{-al2-{-x, w):

д - { - а + х)

или •да„ = 2а)о

у + а - х а

(11.10)

- al2 + x - { - a + x)

В соответствии с уравнениями (11.9) и (11.10) потокосцепление на первом участке EF представим

J --(У.-\-а-х)йу.

-а/2

Аналогично для второго участка

а J а

а/2+х

Окончательно определяем потокосцепление вторичной обмотки

,-а/2+дг а/г

L -aft

(x-y)dy

Выходной сигнал преобразователя

Полученное выражение выходного сигнала для распределенной вторичной обмотки совпадает с выражением выходного сигнала для сосредоточенной обмотки. Это объясняется тем, что и в том и в другом случае при смещении обмотки в каждом витке создается одинаковое приращение потокосцепления, в результате чего суммарные потокосцепления распределенной и сосредоточенной обмоток имеют одинаковые выражения. Однако в распределенной обмотке можно уложить большее число витков.

Нагрузочный режим трансформаторного преобразователя. Вторичная обмотка преобразователя, работающего в системе автоматического управления или регулирования, включается обычно на вход усилительного устройства, поэтому нагрузочным сопротивлением преобразователя является входное сопротивление усилителя, имеющее конечное значение. В результате этого напряжение в режиме нагрузки может значительно отличаться от напряжения холостого хода.

Трансформаторные измерительные преобразователи в отличие от силовых трансформаторов, предназначенных для передачи энергии, работают в ненасыщенном режиме. Следовательно, индуктивные сопротивления первичной и вторичной обмоток, а также сопротивление взаимоиндуктивности можно считать независимыми от режима нагрузки. Электрическая цепь двухобмоточ-ного трансформатора представлена на рис. 11.28.

Запишем уравнения по второму закону Кирхгофа для первичного и вторичного контуров: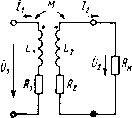

Рис. 11.28. Электрическая цепь двухобмоточиого трансформатора

(11.11)

где R\ и /?2-активные сопротивления первичной и вторичной обмоток; JioL, и А2 = (о/.2-индуктивные сопротивления обмоток; М - взаимная индуктивность обмоток.

Решая уравнения (11.11) относительно тока /2, получаем

(«j-Ь -Ь Ma) (1-Ь Ml)-Ь (<-f )2 Выходное напряжение преобразователя при этом

(11.13)

ГЛАВА 12. ПЕРВИЧНЫЕ ГЕНЕРАТОРНЫЕ ПРЕОБРАЗОВАТЕЛИ

В устройствах автоматики применяются различные первичные генераторные преобразователи (ПГП). Широко используются следующие ПГП: индукционные, пьезоэлектрические, термоэлектрические и преобразователи иа основе эффекта Холла. ПГП осуществляют, как правило, непосредственное преобразование входной величины в выходную в отличие от ППП, у которых измеиение входной величины приводит к измерению какого-либо параметра, что соответственно отражается на значении выходной величины. При наличии дополнительного источника энергии выходная мощность ПГП может быть больше входной, так как в этом случае происходит преобразование иеэлектрической энергии в электрическую.

Термоэлектрические и некоторые преобразователи иа основе эффекта Холла не имеют подвижных частей и к ЭМАА могут быть отнесены условно, однако они непосредственно преобразуют неэлектрическую величину в электрическую и поэтому включены в группу ПГП.

§ 12.1. Индукционные преобразоввтели

Индукционные преобразователи предназначены для измерения линейных и угловых скоростей или перемещений. По принципу действия индукционные преобразователи можно разделить иа две группы; преобразователи со взаимным перемещением катушки и магнита и преобразователи с изменяющейся величиной ноля постоянного магнита.

В преобразователях первой группы сопротивление иа пути постоянного магнитного потока остается неизменным, а индуктированная ЭДС наводится в катушке благодаря линейным или угловым перемещениям катушки в зазоре магнитной системы. При этом в некоторых конструкциях катушка выполняется неподвижной, а перемещается магнитная система. В преобразователях второй группы индуктированная ЭДС наводится в результате изменения магнитного сопротивления цепи при перемещениях подвижной части.

Индукционные преобразователи скорости в качестве входной величины имеют механическую скорость, а в качестве выходной ве-

личины - электрическое напряжение или ЭДС. Преобразователь с взаимным перемещением катущки и магнита изображен на рис. 12.1.

Магнит 4 цилиндрической формы является источником потока, замыкающегося через магнитопровод / и воздушный зазор. Магнитопровод имеет форму полого цилиндра. В воздушном зазоре вдоль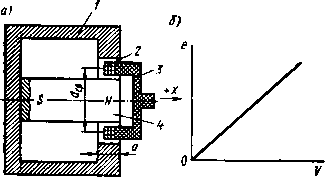

Рис. 12.1. Преобразователь с взаимным перемещением катушки и магнита:

а - прннцнпнльяая схема;

б - характеристика управления

ОСН перемещается сигнальная обмотка 2 в виде кольца. Обмотка залита эпоксидным компаундом 3, что обеспечивает ей прочность и крепление с другими подвижными деталями.

При перемещениях сигнальной обмотки в ней наводится ЭДС

e=-wdФйt, (12.1)

где КУ -число витков обмотки; Ф -магнитный поток, пронизывающий обмотку.

Поток Ф разветвляется на два потока:

Ф=Ф«.г+Фг. (12.2)

Здесь Фвж-поток воздушного зазора, сцеплеииый с витками обмотки и изменяющийся при ее перемещении; Фг - торцовой поток, не зависящий от перемещения обмотки.

Подставляя выражение (12.2) в уравнение (12.1), находим

где V=dx:/d -линейная скорость перемещения обмотки. Учитывая, что dФг/dл: = 0, получаем

е-чюУйФЛх. (12.3)

Поток

Ф«;г=8,ЛйГ,р(а/2-х), (12.4)

где В» -индукция в точках зазора на поверхности цилиндра с ди-234

аметром dcp; dcp -диаметр среднего витка обмотки; а-размер полюса; х - перемещение обмотки. Из уравнений (12.3) и (12.4)

e=nBf,wclV.

Таким образом, наводимая ЭДС прямо пропорциональна линейной скорости.

При синусоидальных колебаниях подвижной части x=Xm.m(at выходной сигнал равен

е = nwBfadpXn cos (12.5)

Из уравнения (12.5) следует, что в этом случае наводимая ЭДС изменяется по косинусоидальному закону и пропорциональна амплитуде и частоте колебаний обмотки.

Преобразователь с изменяющейся величиной поля постоянного магнита изображен на рис. 12.2, а. Магнитная система преобразователя состоит из постоянного магнита 3, магнитопровода 4 и по-

0) 6

Л Фа

1

Рис. 12.2. Преобразователь с измеряющейся величиной поля постоянного магнита:

а - пряяцяпяальная схема; 6 - характеряетяка преобразователя

люсов / И 5. Выходной сигнал снимается с обмотки 2. При прохождении ферромагнитной детали 6 в направлении х (рис. 12.2, а) поток постоянного магнита вначале растет, так как увеличивается проводимость между магнитной системой и деталью 6, а затем поток магнита уменьшается. Далее следует опять нарастание потока и вновь его уменьшение. В сигнальной обмотке наводится ЭДС, пропорциональная скорости изменения потока (рис. 12.2,6):

e=-wйФйt=-wVйФйx. (12.6)

Из уравнения (12.6) следует, что наводимая ЭДС прямо пропорциональна линейной скорости и производной потока, пронизывающего обмотку, по перемещению. Потоки рассеяния при этом не учитываем. Форма кривой ЭДС близка к синусоидальной. Выходной сигнал преобразователя может быть включен через выпрямительный мост на измерительный прибор постоянного тока. Если на выход обмотки подключить счетчик импульсов, то по его показаниям можно определить также количество прошедших деталей.