в поле; N, цг -размагничивающий фактор и относительная магнитная проницаемость материала тела. Учитывая

(9.4>

{9.5>

при цг> 1 получим

Используя (9.2) -(9.5), из (9.1) имеем

P,,= VB(dB/dz)l(o). (9.6)

В случае использования ферромагнитного тела в виде шара с радиусом г (размагничивающий фактор для шара равен 1/3) имеем

Р,„,=АлгВ(дВ/дг)/о- (9.7)

Как следует из выражения (9.7), в точках пространства, где модуль или градиент модуля вектора индукции равны нулю, электромагнитная сила тоже равна нулю, причем в точках с максимальным значением модуля вектора индукции имеет место устойчивое, а в точках с минимальным (в том числе с нулевым) значением модуля вектора индукции- неустойчивое равновесие. Тело смещается в сторону увеличения индукции. Из этого следует, что для реализации скачкообразного перемещения подвижного КС в виде плунжера или шарика (т. е. для обеспечения релейного процесса коммутации) с помощью подвижных постоянных магнитов необходимо синтезировать на основе этих магнитов в пространстве распределение магнитной индукции, подобное показанным на рис. 9.4, а или б, и перемещать это распределение относительно подвижного КС. Распределение поля,

-с ,, как на рис. 9.4,а, имеет, на-

Рис, 9.5. Магнитное поле аксиально-намаг- „„,... „„ „ ..

ниченмого кольцевого постоянного мапшга пример, аксиально-намагни-

(а) и управление им Н1ариковым МК {б, в) чемныи кОЛЬЦевОЙ ПОСТОЯН-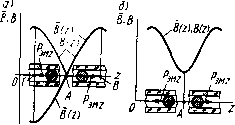

Рис. 9.4. Кривые распределения магнитной индукции, при которых возможна реализация скачкообразного перемещения магнито-мягкого подвижного КС в шариковом МК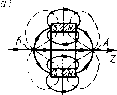

ный магнит вдоль его продольной оси z (рис. 9.5). Такое распределение обеспечивается наличием двух особых точек поля (Л и 5), в которых происходит ветвление сепаратрис и магнитная индукция равна Нулю. При переходе через эти точки вектор магиитной индукции по оси Z меняет направление. Управление, на- а) пример, шариковым МК с ,

помощью такого постоянно-го магнита осуществляется

следующим образом. Если шарик на оси z расположен между точками Л и S, то на него действует электромагнитная сила вправо (см. рнс. 9.5,0 и на рис. 9.4, а тот же участок), прижимая его к правой паре неподвижных КС (рис. 9.5,6). Перемещение постоянного магнита вправо с переходом точки Л через шарик вызывает скачкообразное перемещение шарика влево до замыкания другой пары неподвижных КС (рис. 9.5,в).

Управление плунжерными и шариковыми МК может осуществляться и системой постоянных магнитов, причем последние часто выполняют функцию «магнитной пружины», основанной на реализации магнитной опоры. Примером такой системы служат два аксиально и встречно намагниченных кольцевых постоянных магнита (рис. 9.6). При значительном удалении А постоянных магнитов друг от друга (примерно более наружного диаметра) их магнитное поле в плоскости про--вдльной проекции характе-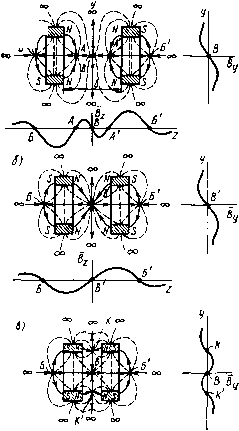

Рис. 9.6, Картины поля и кривые распределения индукции вдоль осей г к у двух кольцевых постоянных магнитов, намагниченных встречно-аксиально: а - при A=Ai; б - при A2<Ai; в - при Дз<д2

ризуется шестью особыми точками: пятью точками А, А, Б, Б, В, расположенными на продольной оси z, и одной точкой - в бесконечности (рнс. 9.6, а), В каждой из этих точек наблюдается ветвление четырех сепаратрис, изображенных сплошными линиями.

Градиентные кривые, сходящиеся в этих точках, показаны штриховыми линиями. По мере сокращения расстояния между магнитами точки А к А сближаются с точкой В и, наконец, сливаются с ней, образуя по характеру более сложную особую точку В, в которой происходит ветвление уже восьми сепаратрис (рис. 9.6,6). При дальнейшем сближении магнитов на поперечной оси у между ними появляются две особые точки: К н К (рис. 9.6,в). В этом случае, так же как и при положении магнитов, соответствующем рис. 9.6, а, имеется особая точка В, однако направление разветвляющихся в ней сепаратрис меняется на противоположное. Особые точки /С и /С являются следами кольцевой особой кривой, представляющей собой геометрическое место множества подобных особых точек. По мере перемещения магнитов относительно друг друга по оси 2 диаметр этой особой кривой (а соответственно и координаты особых точек К и К) меняются. Анализ кривых распределения индукции вдоль осей z i\ у, приведенных на рис. 9.6, а-в, показывает, что перемещением таких магнитов по оси z можно осуществлять переключение от одного до пяти плунжерных или шариковых МК, расположенных на оси z, или множества таких МК, расположенных радиально в вертикальной плоскости посередине между магнитами.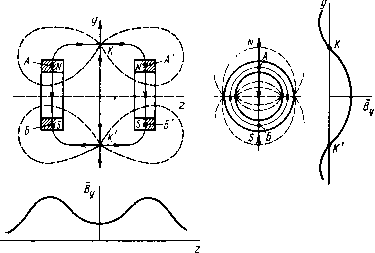

Рис. Р.7. Картина поля н кривые распределения индукции вдоль осей г и у двух кольцевых постоянны.х магнитов, имеющих «бочоночное» намагничивание в одном направлении

Кольцевые постоянные магниты намагничиваются не только аксиально. Существуют радиальный, диаметральный и «бочоноч-иый» (встречно-азимутальный) способы их намагничивания. Поля таких постоянных магнитов, естественно, отличаются от полей,

изображенных на рис. 9.6. Так, поле системы из двух магнитов с «бочоночным» намагничиванием (рис. 9.7) характеризуется шестью особыми точками, две из которых (К и К) находятся вне магнитов в вертикальной плоскости между ними, а четыре других (Л, А, Б, Б) - в теле магнитов в плоскости сечения, где образованы полюса. Такая система по оси у образует распределение магнитной индукции, соответствующее рис. 9.4, а, а по оси z - соответствующее рис. 9.4, б.

Магнитные поля с перемещающимися в пространстве особыми точками для управления МК могут создаваться не только кольцевыми, но и другими видами постоянных магнитов, например двумя встречно намагниченными стержневыми магнитами, а также электромагнитами.

§ 9.3. Ферриды

Как было показано в § 8.3, при определенном расположении постоянных магнитов относительно МК последние будут находиться в замкнутом состоянии после снятия сигнала с обмотки управления, т. е. будет реализовываться функция «память». Однако длительность управляющего поля в таких аппаратах с МК не должна быть меньше десятых долей - единиц миллисекунды. Необходимость уменьшения длительности управляющего поля до микросекундного диапазона, а также ряд схемных и других требований, предъявляемых к координатным соединителям автоматических телефонных станций (АТС) и к устройствам систем контроля, привели к созданию новых быстродействующих электромеханических коммутационных аппаратов - запоминающих магиитоуправляемых контактных устройств (ЗМКУ). или ферридов [43], сочетающих в себе свойства МК и элемента магнитной памяти (ЭМП). Второе название -ферриды более распространено. Оно появилось от слияния двух терминов: феррит и рид свич (транскрипция английского термина reed switch - язычковый выключатель), так как первоначально ЭМП выполнялись из магнитотвердых ферритов. В современных ферридах ЭМП изготавливают из среднекоэрцитив-ных (Яс==2+6 кА/м) металлических ферромагнетиков с более высокими, чем у ферритов, значениями остаточной индукции (Sr= = 1,6-1,8 Тл) и коэффициента прямоугольности петли гистерезиса, равного 0,85-0,9. Если ЭМП располагается вне баллона МК, то такое исполнение классифицируется как феррид с внешним ЭМП. Роль ЭМП могут играть контактные сердечники МК или их части. Такие конструкции классифицируются как ферриды с внутренним ЭМП. В отечественной литературе МК, контактные сердечники которых выполняют роль ЭМП, называются гезаконами (см. § 7.1).

Простейшие ферриды. Схемы простейших ферридов с внешним и внутренним ЭМП приведены соответственно на рис. 9.8, а, б. В первом случае (рис. 9.8, а) рядом с МК 1 расположен ЭМП 4

с полюсами 2 и 5. В схеме феррида с внутренним ЭМП (рис. 9.8, б) КС помимо обычных функций выполняют также функцию магнитной памяти. В обеих схемах магнитная память феррида создается и разрушается с помощью соответствующих импульсов тока, подаваемых в обмотку 3. Для срабатывания МК в обмотку подается импульс намагничивающего тока ia (рис. 9.8, в). Контактные сер-

а) 2-

-Г"

Рис. 9.8. Принципиальные схемы (а, б) и управляющие импульсы (в) простейших ферридов

дечники замыкаются и после снятия импульса тока остаются в замкнутом состоянии за счет остаточного магнитного потока ЭМП. Для возврата МК в обмотку подается импульс размагничивающего тока 1р. Амплитуда и длительность размагничивающего импульса должны быть строго определенными, чтобы не произошло перемагничивание ЭМП в противоположном направлении и повторное (ложное) замыкание КС.

Параллельные и последовательные ферриды. Недостаток, присущий однообмоточным ферридам и заключающийся в требовании калибровки импульсов при возврате, может быть ликвидирован следующими способами [43]: 1) размагничиванием ЭМП переменным затухающим магнитным полем; 2) ортогональным перемагни-чиванием ЭМП; 3) взаимным шунтированием участков ЭМП; 4) встречным намагничиванием участков ЭМП.

Первый способ общеизвестен. Второй способ к настоящему времени не получил широкого распространения, поэтому мы проанализируем только два последних решения. Третий способ конструктивно реализуется в виде параллельного феррида, четвертый - в виде последовательного феррида.

Принцип действия простейшего параллельного феррида с внешним ЭМП иллюстрируется рис. 9.9, а. Элемент магнитной памяти в данном случае состоит из двух полуколец с размещенными на них

обмотками, в которые подаются импульсы тока. Принцип действия последовательного феррида с внешним ЭМП может быть легко понят на рис. 9.9, б. Примером последовательной конструкции является также феррид с внутренним ЭМП, имеющий две обмотки управления (рис. 9.10). Сплошные стрелки показывают направление МДС обмоток при срабатывании феррида, штриховые - при возврате. Магиитомягкий шутШ (рис. 9.9,6 и 9.10) улучшает условия возврата последовательных ферридов [43].

Все рассмотренные ферриды имеют общую черту - при их управлении требуется перемагничивание в противоположных направлениях преимущественно по полному циклу петли гистерезиса хотя бы одной из частей ЭМП. Более подробное

описание различных па- р„с. 9.9. Принципиальные схемы параллель-

раллельных и последова- ного (а) и последовательного (б) ферридов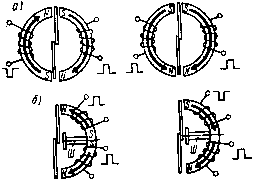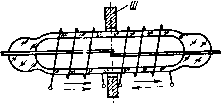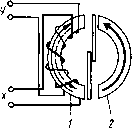

Рис. 9.10. Двухобмоточный феррид с внутренним ЭМП

Рис. 9.11. Параллельный феррид с аддитивным управлением. На ЭМП / стрелками показано:

---срабатывание:

...... - возврат

тельных ферридов, а также анализ ортогонального способа управления приведены в специальной литературе [43].

Способы управления ферридами в матричных системах АТС.

Распространение получили три способа: аддитивный (суммирующий), дифференциальный и безгистерезисный.

Прн аддитивном управлении число витков, амплитуда и длительность импульса тока в каждой из обмоток (соответствующей колонке или ряду коммутационной матрицы) выбираются таким