Часто в одном реле используются как внешний, так и внутренний дополнительные магнитопроводы.

На основе МК можно создать не только одноконтактное (см. рис. 8.1), но и многоконтактное реле, расположив, например, в обмотке несколько коммутационных элементов (рис. 8.8). В многоконтактном герконовом реле коммутация отдельных выходных цепей в общем случае происходит при различных значениях МДС обмотки, что определяется тремя причинами. Во-первых, МК даже одного типа отличаются друг от друга по МДС срабатывания и МДС возврата, измеренными в обмотке одноконтактного реле (см. рис. 8.1). Во-вторых, магнитное поле в местах расположения различных МК многих исполнений многоконтактных реле неодинаково, поэтому раньше замыкаются МК, которые (при прочих равных условиях) находятся в областях с большей напряженностью поля. В-третьих, замыкание одного МК приводит к магнитному шунтированию других и поэтому требует дополнительного увеличения МДС обмотки для замыкания всех МК реле. Следует иметь в виду, что магнитное шунтирование здесь имеет более сложную природу, чем шунтирование в параллельных активных электрических цепях. При замыкании одного из МК не только увеличивается внутренняя магнитная проводимость этого МК, но и возрастает его внешняя магнитная проводимость, при этом внешняя магнитная проводимость остальных МК уменьшается.

§ 8.3. Поляризация герконовых реле

Поляризация осуществляется с целью изменения чувствительности и коэффициента возврата реле, создания на основе замыкающего МК реле с размыкаемым контактом. Кроме того, как было указано в § 7.2, существуют МК, которые без поляризации вообще не могут работать (см. рис. 7.10).

Поляризующий магнитный поток в МК создается специальной обмоткой или постоянным магнитом. Влияние поляризации постоянным магнитом на функциональные статические характеристики сухого симметричного язычкового замыкающего МК (рис. 8.9, а) иллюстрируется диаграммой рис. 8.9, б. При отсутствии поляризации (на диаграмме обозначено вертикалью А) значения fcp и Рв не зависят от полярности питания обмотки управления (магнитным гистерезисом пренебрегаем). Небольшая поляризация (вертикаль Лп1 на диаграмме) приводит к уменьшению значений +Рср и +Рв, соответствующих одинаковому направлению в рабочем зазоре МК магнитных потоков от поляризующего магнита и обмотки (назовем поляризацию при таком направлении потоков «положительной»), и увеличению значений «-Рср\» и «-Рв\у>, соответствующих встречному направлению этих потоков («отрицательная» поляризация). «Положительная» поляризация уменьшает коэффициент возврата, а «отрицательная» увеличивает. Увеличение поляризации до определенной величины приводит к состоянию (обозна-

чено вертикалью Л „г на диаграмме), характеризуемому удержанием МК в замкнутом положении при снижении тока в обмотке до нуля после замыкания МК при некотором значении «-+-F» (точка / на вертикали Лпг). Для размыкания МК необходимо увеличивать ток в обмотке от нуля в противоположном направлении (точка 2 на вертикали Лпг).

Дальнейший рост поляризации приводит к замыканию МК полем постоянного магнита при отсутствии тока в обмотке. Это дает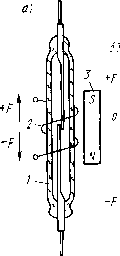

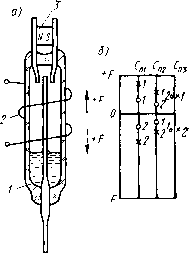Рнс 8 9 Поляризованное реле с сухнм Рнс. 8.10. Поляризованное реле с симметричным язычковым замыкающим переключающим жндкометалличе-МК (а) н диаграмма его функцнональ- ским МК (а) и диаграмма ных характеристик (б): его функциональных характерис-

; МК- 2 -обмотка; 3 - поляризующий маг- ТНК (б):

нит; X-замыкание МК; О-размыкание МК ; -МК; г -обмотка; J - поляризук>-

щий магнит; X - замыкание КС; О - размыкание КС

возможность реализовать на основе замыкающего нейтрального МК реле с размыкающим контактом (вертикаль В на диаграмме). Размыкание МК происходит при увеличении МДС от нуля в «отрицательном» направлении (точка 2 на вертикали В). При последующем снижении \-Р\ МК замыкается (точка J на вертикали В).

При реализации состояний А„2 и В следует иметь в виду, что рост МДС -F после размыкания МК (точки 2 на вертикалях Лп2 и В) приводит при ее некотором значении к изменению направления суммарного магнитного потока в рабочем зазоре, а дальнейшее увеличение -F вызывает замыкание МК (точки 3 на вертикалях Лп2 и В). При последующем снижении \-Р\ МК размыкается (точки 4 на вертикалях Лп2 и В).

На рис. 8.10, а изображен поляризованный переключающий ЖМК. Поляризация осуществляется постоянным магнитом, расположенным между выводами неподвижных КС. При отсутствии постоянного магнита подвижный переключающий КС находится симметрично между неподвижными КС. Возможные функциональные характеристики реле (в зависимости от исполнения) с МК такого вида иллюстрируются диаграммой рис. 8.10, б, на которой точки / соответствуют замыканию и размыканию одного из неподвижных КС, а точки 2 - другого ,КС. Реле может быть одностабильным (вертикаль Сщ на диаграмме рис. 8.10, б), когда после снятия управляющего сигнала {«+F» или «-Fi>) переключающий КС занимает нейтральное положение между неподвижными КС, или двустабильным, когда в двух крайних положениях переключающего МК осуществляется его магнитная блокировка. Двустабильное реле может быть в свою очередь трехпозиционным или двухпози-ционным. В трехпозиционном реле (вертикаль Сп2 на диаграмме) при достижении током в обмотке значений возврата (в области «-4-/"» или «-F») переключающий КС размыкается с одним из неподвижных КС и после затухающих колебаний остается между неподвижными КС. В двухпозиционном реле (вертикаль Съ на диаграмме) переключающий КС при токах возврата «перелетает» от одного неподвижного КС ко второму и остается в замкнутом состоянии с последним после снятия сигнала в обмотке.

§ 8.4. Расчет магнитной системы и функциональных параметров геркоиовых реле

Рассмотрим в качестве примера методологию расчета герконового реле, картина магнитного поля которого в продольной проекции изображена на рис. 8.3. Простейшая рас-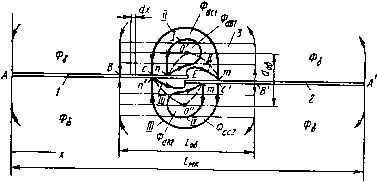

Рис. в.П. Топографическая модель магнитного поля реле с одним симметричным язычковым замыкающим МК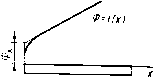

Рис. 8.12. Определение концевого магнитного потока

четная топографическая модель поля такого реле, полученная иа основе анализа результатов аналогового и физического моделирования [37], приведена на рис. 8.11. В этой модели принято, в частности, что МДС обмотки сосредоточена в бесконечно тонком слое, расположенном по окружности, образованной средним диаметром обмотки doe.

При математическом описании топографической модели (т. е. при математическом моделировании) на основе анализа результатов исследований [37] удельная (на единицу длины КС) внешняя магнитная проводимость Явш принята постоянной вдоль КС. Сделано также допущение о бесконечно большом значении магнитной проницаемости материала КС, что при условии работы на «линейном» участке кривой намагничивания пермаллоев, используемых для изготовления КС и обладающих высокой максимальной магнитной проницаемостью, не вносит значительной погрешности в расчет.

Рабочий магнитный поток системы на основе рис. 8.11 и 8.12 определяется как

Ф« = Фк + Флй + Фас. (8.18)

где Фк - концевой поток (рис. 8.12), учитывающий часть потока Фб, входящую в торец внешнего конца КС, и отличие от линейного характера распределения магнитного потока в КС [Ф=1(х)\ у этого конца [37]; Флв и Фвс - магнитные потоки, «входящие» в КС соответственно иа участках АВ м ВС (рис. 8.11).

Для потока Фк имеем

(8.19)

где Лк - концевая магнитная проводимость, а для потока Флв имеем

<-U(/=-t/«.„)/2. (8.20)

При нахождении выражения для потока Фвс необ.ходимо сначала составить дифференциальное уравнение, так как линии магнитной индукции этого потока ие охватывают все витки обмотки (рис. 8.11). Это дифференциальное уравнение имеет вид

йФвс=Чш [/(mk-2x) „6-t/„.„] dx. После его интегрирования получаем

"С

Фвс=(

=Ки {р [к.хс -х1- /„к (/„к - +(/«к-ит/и -

-/м.„1С-(мк-/об)/2]}.

(8.21) 179

(8.22)

(8.23)

Учитывая (8.18) -(8.21) и (см. рис. 8.5) формулу

А„,= 1 ?м.вт=Фе/«.вт. после преобразования получаем

ф р. Ак + Хат [мк-<с - -С ~ (мк - /об)/4];/об

Из (8.22) и (8.23) имеем

п* -ii i + [мкс - 4 - (мк-/об)/4]/Ак/об

f-jf*.Bx-u „/j ----- • (o-i;

Как показано в § 8.1, при анализе рассматриваемой магнитной системы, для наиболее часто встречающихся случаев можно пренебречь потоками рассеяния Фвь Фггвг, Фас, и Фйсг (см. рис. 8.3 и 8.11). При этом Ф1=Фв (см. рис. 8.5 и 8.11). Тогда из (8.4) и (8.23) получаем выражение для суммарной магнитной проводимости, приведенной к полной МДС обмотки по потоку:

Ак + Km [Uk-c ~ 4 ~ (мк - /об)/4] о6 1 + (Кш-с + Ак)/Авт

Из (8.23) и (8.24) с учетом (см. рис. 8.5) формулы

Кш = 1 ?«.вш = ФЛ - «.вт) (8.26)

Л2;ф=-

(8.25)

(8.27)

находим выражение для внешней магнитной проводимости

{С-[мкС-4-(«к-обт] об/Авт

При 6=0 (соответственно Лвт=оо и Хс=/мк/2-а/2«/мк/2) (см. рис. 8.11) имеем

Авш=Лк+}вш(„к/2-и4).

Как следует из (8.9), для определения магнитной проводимости Лгчг надо найти значения W, Wm или L. Найдем выражение для Лгчг рассматриваемой магнитной системы через магнитную энергию. Последняя в случае пренебрежения потоками рассеяния, согласно рис. 8.11, определяется суммой

W„ = W,+Was + Wsc, (8.28)

где Wk, Wab и Wbc - составляющие магнитной энергии системы, соответствующие потокам Фк, Фаз и Фес-

Эти составляющие находятся следующим образом:

Гк=Фк/="/2=Лк (F - F/2; (8.29)

Wab=abF/2=X, (/„к - U) (F - f/„.BT) Ff4; (8.30) Швc=<iФвcF (/„. - 2x)/(2Uy,

WBc\<iWBc= j uWbc=FKA4FxIi01o6)--

- (2FUU - xl + /„K (FIJU - «.bt) Xc --F{K,-K,YiQUMlu.-U)4FUU-U..J2)l2 -

- («k - 06) (Fljl - f/„.,,)/2]/(2/„6). (8.31)

Магнитная проводимость Лгчг определяется из (8.9) с учетом (8.24) и (8.28) -(8.31):

Л=Лк(1 -A)-f Х, [/„к/2-W3-(4/6-44/3 + -f 21% - llc)lll(> - А («к/2 - об/4 - /мк/(4/„б) --4 „6 + mkVU]. (8.32)

где безразмерная величина

Л={Лк + Х, [мк-«с-4 - («K-U/4I/U/(AK + A„-f Х„„д:с)-

(8.33)

При (/мк-/об)/2 имеем Л1чг=Л1ф, так как линии индукции потока Фе охватывают в этом случае все витки обмотки.

Значения проводимостей Явш и Лк, входящих в основные уравнения (8.23) -(8.25), (8.27) и (8.32), находятся из формул

X,,=(0,724-f 4,92/;:-f 0,314/:б)10-«, Гн/м, (8.34)

Лк=Х«Л. Гн, , (8.35)

XK=(0,378-fO,37/;c*-f 1.820*6 - 17,04ло*б) 10-«, Гн/м. (8.36)

Здесь рс - периметр поперечного сечения КС, м; /*об=/об мк, *об=об мк, р*с = Рс мк -безразмерные величины.

В эмпирических выражениях (8.34) и (8.36) допустимое варьирование факторов находится в следующих пределах: Рс* = 0,075± ±0,042; /*об=0,4±0,1; d*o6=0,125±0,033.

При заданных размерах магнитной системы (/мк, рс, /ов, об) и рассчитанных А,вш и Лк в уравнениях (8.23) -(8.25), (8.27) и (8.32) неизвестными являются координата Хс и проводимость Лвт, представляющая собой функцию от Хс. Для нахождения Хс и Лвт используется известное положение о том, что линии магнитной индукции при заданных параметрах магнитной системы (размеры, материал магиитопровода и значение МДС обмотки) принимают в пространстве единственно возможную конфигурацию. Эта конфигурация соответствует максимуму магнитной энергии поля [максимуму потокосцепления, индуктивности или проводимости Aiv- см. (8.9)] этой системы.