Суммарный магнитный поток всей системы Ф1 = Фб + 2(Фйв +

+ Odc).

Если известно распределение магнитной индукции вдоль граней А н Б контактного сердечника (рнс. 8.4), то с помощью формулы Максвелла можно найти значения электромагнитных сил Рэм.а и Рзм.б (рнс. 8.4), действующих на каждый КС в противоположных направлениях. Из рис. 8.4 следует, что на участках граней А н Б от наружных концов КС примерно до точки п распределение индукции практически одинаково, в области же перекрытия а КС значения индукции на грани Б существенно больше, чем на грани А. Из этого следует, что Рмэ. >Рэм.а, а результирующая электромагнитная сила Рэм=Рэм. б-эм.А направлена в сторону сближения КС. Прн насыщении последних картина распределения индукции вдоль нх поверхностей меняется не только количественно, но и качественно. Прн этом может существенно измениться и соотношение сил Рэм.А и Рэм. б •

При достаточно полном анализе рассматриваемой системы с применением методов теории цепей необходимо использовать дифференциальные уравнения с учетом того, что удельные параметры такой системы (МДС обмотки и магнитная проводимость потока Фив на единицу длины обмотки, магнитная проводимость потоков Фе и Фс на единицу длины КС и магнитное сопротивление единицы длины КС), строго говоря, переменны. Кроме того, прн составлении дифференциальных уравнений в пределах обмотки необходимо иметь математическую связь текущего (по длине системы) значения МДС обмотки с точками вхождения в КС линии магнитной индукции, охватывающей эту часть обмотки. Решение задачи в таком виде чрезвычайно сложно, поэтому делают ряд допущений, обоснованных данными аналогового и физического моделирований

(см. § 8.4). В результате удается провести расчет с высокой точностью.

В данном параграфе мы ограничимся рассмотрением простейших выражений, которые позволят нам, однако, судить о взаимосвязи некоторых параметров реле с его геометрическими факторами.

На рис. 8.5 изображена упрощенная схема замещения магнитной цепн анализируемой системы, составленная прн пренебрежении магнитным сопротивлением КС. На схеме Рм.вт - магнитное сопротивление внутреннего участка цепн на пути прохождения потока Фе между внутренними концами КС; /м.вт=фм1-<рм2 - магнитное напряжение на этом сопротивлении; Ям.вш - магнитное сопротивление внешнего участка цепи на пути прохождения потока Фе между внешними участками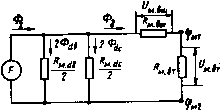

Рис. 8.5. Упрощенная схема замещения магнитной цепи симметричного реле с язычковым замыкающим МК

КС, приведенное по потоку к магнитному напряжению им.вш=Р- -Um.bt; Rm.cIb и Pw.dc -приведенные по потоку к полной МДС обмотки магнитные сопротивления на путях прохождения соответственно потоков Фdв и Фdc.

Суммарная магнитная проводимость, приведенная к полной МДС обмотки по потоку, определяется выражением

Л,ф= [А,гКшККг+Кш)\ +2 (Л, + ЛД (8.3)

где Лет, Леш, Ada н Ade - магнитныс проводимости, соответствующие указанным выше магнитным сопротивлениям. Суммарный магнитный поток в системе

Ф,=/=-Л,ф. (8.4)

Исследования показывают, что для наиболее часто встречающихся на практике соотношений размеров реле (обмотка имеет малую толщину по сравнению с длиной, а ее внутренний диаметр несущественно превышает наружный диаметр баллона) величина 2(ФdE+Фdc) составляет не более 15-20% от Ф, если КС не насыщены. Прн этом, как следует нз (8.2), можно приближенно принять Фз: = Фтах = Фв. В ЭТОМ случае НЗ схсмы рис. 8.5 получаем

Ф.= Фтах = Фб = А,,Лз,/(Леш + Л„). (8.5)

Основные расчетные соотношения. Значения максимального магнитного потока в КС дает возможность определить результирующую электромагнитную силу Рэм по эмпирическим формулам, например, вида [39]

Яэм=Фтах/21ьоа*{1 + [*u + *2s (Л/й) 4-39 (8.6)

Здесь b и /г -ширина и толщина КС в области нх перекрытия а; ki3, и /гзэ - безразмерные эмпирические коэффициенты, зависящие от соотношения размеров б/а и h/b, а также от максимальной индукции в КС [39].

Результирующую электромагнитную силу можно также найти по энергетической формуле, которая для неизменного тока имеет вид [40]:

P, = -dWJdb, (8.7)

где Wko-коэнергня магнитной системы.

Для некоторого заданного значения тока / коэнергня равна

где W - потокосцепление системы.

Для линейной зависимости потокосцепления от тока (индуктивность L системы не является функцией от тока) имеем

P3„=-/=2dAW(2d8). (8.8)

в этом выражении Azv (см. § 1.2) -суммарная магнитная проводимость системы, определяемая через потокосцепление W, запасенную магнитную энергию Wm системы нли индуктивность обмотки в этой системе:

(8.9)

где W - число витков обмотки.

Для линейной системы WM=lFbo.

Таким образом, для определения электромагнитной силы по энергетическим формулам (8.7) и (8.8) необходимо рассчитывать потокосцепление системы.

В общем случае Лз:ч<;АгФ (см. гл. 1). С сокращением площади поперечного сечения обмоткн отличие этих проводимостей уменьшается. Прн идеализированной замене обмоткн одним витком провода с бесконечно малым диаметром имеем А1ч = А1ф.

Механическая сила упругости КС (рнс. 8.2) может быть выражена как

мх=с„р(8„-8).

(8.10)

Здесь Спр -приведенная жесткость двух КС, характеризуемая на рнс. 8.2 углом

a = arctg(c„p«j/«p),

где Лб и Лр -масштабы по осям абсцисс и ординат на рнс. 8.2 (размерность соответственно м/мм и Н/мм).

Можно легко показать, что прн равенстве результирующих электромагнитных снл, действующих на каждый нз двух КС, приведенная жесткость этих КС определяется как

пр = 12/(1 "Гг)-

В формуле с, н С2 - жесткости отдельных КС.

Для точки касания характеристик f, (б) н Рэм=/2(б)

(рнс. 8.2), т. е. 6=бср и F=Fcp, определимы следующие равенства:

Р.. = Р..\ dP3„/d8 = dP„,/d8.

Прн учете (8.8) и (8.10) для 6=бср эти равенства преобразуются к следующему виду:

-Flp (dAs/d8)8p/2 = с„р (8„ - 8,р);

-/="cp(d2AiT/d82)j 2=-с„р.

(8.11) (8.12)

Из (8.11) находим выражение для МДС срабатывания реле: ср = V -2Спр (8„ - Sep) {йА.фЬ\\ (8.13)

Как следует из (8.13), для определения МДС срабатывания необходимо найти величины бср и (dAi4/d6)ej. Разделив (8.11) на (8.12), получим выражение для бср:

(dA,,r/d8)5

ср=8и+ • (8.14)

Если определить зависимости Ai,-, dAi/de и dAi/de от б, то нз (8.14), используя итерационный метод расчета, можно для заданного б„ найти величину бср. Зная бср и соответствующее ему значение (dAi4/d6)e<.p, по (8.13) находится МДС срабатывания.

При возврате реле (б=бк) справедливо равенство Рзч = = Рмх.к; отсюда, учитывая (8.8) и (8.10), имеем

/=-B(dAsWd8)8/2=c„p(8„-8,). (8.15)

Из (8.15) находится выражение для МДС возврата реле

-2c„p(8„-8,)(dAsWd8)r;, (8.16)

а нз (8.13) и (8.16)-выражение для коэффициента возврата

K-fJfcp= ViK - К) (8„ - срГ (dA,Wd8)5p(dA,WdS)r;. (8.17)

Используя (8.1), (8.8) и (8.10), можно получить также формулу для контактного нажатня прн произвольной МДС, а с добавлением (8.13) - для контактного нажатия прн fcp.

§ 8.2. Применение дополнительных магиитопроводов в герконовых реле. Многоконтактные герконовые реле

Для изменения параметров герконовых реле (МДС срабатывания, коэффициента возврата и др.), а также для экранирования этих реле от воздействия посторонних магнитных полей широко используются внешние (по отношению к обмоткам) дополнительные магнитопроводы. На рнс. 8.6, а изображена одна нз возможных картин магнитного поля реле с таким магнитопроводом, выполненным в виде скоб 3 н 4, находящихся под одним и тем же магнитным потенциалом (фмз = фм4). Внутри сепаратрис / и VIII расположены линии нндукцни потоков рассеяния, проходящих только по воздуху. Между сепаратрисами /- {VII-VHI) проходят потоки рассеяния, замыкающиеся также и через КС / (КС 2). Область, ограниченная сепаратрисами - /, характеризует поток рассеяния, замыкающийся через КС 1, пространство между КС 7 и скобой 3, скобу 3 и пространство между скобой 3 и КС 1. Область, ограниченная сепаратрисами VI-VII, характеризует поток рассеяния, замыкающийся через КС 2, пространство между КС 2 и скобой 4, скобу 4 н пространство между скобой 4 и

КС 2. Между сепаратрисами III-IV расположена область потока, проходящего через КС 2, воздух, скобу 3, воздух и КС 7, а между сепаратрисами V-VI расположена область потока, проходящего через КС 2, воздух, скобу 4, воздух и КС I. Область между сепаратрисами IV-V во внешнем пространстве и в рабочем зазоре соответствует потоку, проходящему через оба КС, но не связанному со

Рис. 8.6. Картины магнитного поля герконового реле с внешним магнитопроводе м

скобами 3 и 4. Наличие двух дополнительных ферромагнитных деталей приводит, естественно, к четырем новым особым точкам {р, р на скобе 3 м q, q на скобе 4).

Рассмотренная картина поля не является единственно возможной для такой конструкции реле, даже если скобы 3 vi 4 находятся под одним и тем же магнитным потенциалом. На рис. 8.6, б, в приведены верхние части еще двух возможных картин поля при фмз - = фм4. Первая из них (рис. 8.6, б) характеризуется слиянием сепаратрис / и , чго свидетельствует об отсутствии потока рассеяния, проходящего, исключая воздух, только по КС 1.

На второй картине (рис. 8.6, в) этот поток также отсутствует, но имеется новый вид потока рассеяния (между сепаратрисами / и ), замыкающийся только на скобу 3. Таким образом, картина поля, представленная на рис. 8.6, б, является граничной между картинами, изображенными на рис. 8.6, а, в. Внешний дополнительный магнитопровод при достаточно близком расположении концов скоб 3 V. 4 с КС и отсутствии насыщения последних уменьшает МДС срабатывания и коэффициент возврата реле за счет роста внешней магнитной проводимости. Однако при больших начальных зазорах, когда срабатывание происходит в условиях насыщения КС, применение внешних дополнительных магнитопроводов с целью повышения чувствительности реле не дает положительного

результата и может даже снизить чувствительность из-за роста потоков рассеяния, замыкающихся на магнитопровод.

Для изменения параметров реле используются также внутренние (по отношению к обмотке) дополнительные магнитопроводы. Одна из схем построения реле с таким магнитопроводом в виде двух ферромагнитных трубок приведена на рис. 8.7, а. На рис. 8.7, б дана эксперимен-

тальная зависимость МДС срабатывания увеличенной физической модели такого реле от расстояния \ между ферромагнитными трубками. При малых % трубки шунтируют рабочий зазор МК, что

10 20 30 0 50 60 70 ,мм

Рис. 8.7. Геркоиовое реле с внутренним магнитопроводом

Рис. 8.8. Многоконтактное герконовое реле серии РПГ:

/ - пластмассовый кожух; 2 -обмотка: J - ферромагнитный экран; •* - .МК; 5 - каркас обмотки; 5 -скоба; 7 - пластмассовые колодкн; 8 - резиновые трубки; « - основание

Приводит к увеличению Fcp по сравнению с вариантом, когда такого рода дополнительный магнитопровод отсутствует (с,= оо). При больших же g трубки увеличивают внешнюю магнитную проводимость на пути прохождения рабочего магнитного потока, и чувствительность реле повышается.