Зная ucp, *мэ, kyz, J, с и ЭДС источника питания бвш обмотки, используя (6.10) и принимая ism=esm/ (R+Ram), можно найти время срабатывания ср реле. Это время снижается с ростом коэффициента запаса по току срабатывания iWcp (рис. 6.2, г).

Расчет динамических характеристик реле существенно услож- няется при учете собственной индуктивности обмотки, взаимной индуктивности обмотки с металлической рамкой и провала контактов.

Магнитоэлектрические реле с подвижной рамкой высокочувствительны (минимальная мощность срабатывания достигает Ю-" Вт), однако время их срабатывания сравнительно велико (порядка 0,1 с). К магнитоэлектрическим можно отнести магнитогидродинамические реле, в которых подвижным токопроводом является жидкий металл, например ртуть.

Электродинамкческое реле отличается от магнитоэлектрического реле только тем, что в нем вместо постоянного магнита применяется обмотка с током.

Ферродинамическое реле - это электродинамическое реле, в котором взаимодействие двух систем проводников с током усиливается наличием ферромагнитных деталей.

Принцип действия ферродинамического реле иллюстрируется на рис. 6.3. На полюсы магиитопровода / намотана обмотка 2, по которой проходит постоянный ток /. Симметрично между полюсами находится ферромагнитный сердечник 3. В рабочих зазорах размещается рамка с обмоткой 4. При протекании по обмотке 4 постоянного тока h его взаимодействие с магнитным полем, создаваемым в рабочих зазорах обмоткой 2, вызывает поворот рамки, направление которого определяется правилом левой руки. При допущении линейности магнитной системы и равномерности поля в рабочих зазорах вращающий момент, действующий на обмотку 4,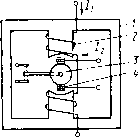

Рис. 6.3. Принципиальная схема ферродинамического реле

(6.11)

где йфд - коэффициент пропорциональности.

Если обмотки питаются синусоидальным переменным током lii=/mi sin (0 и J2=/m2 sin(cu/-ф) ], ТО при вышеуказанных допущениях мгновенное значение вращающего момента

.р / = фдт1т2 Sin О)/• sin (О)/ - (f>) =

= *ФдЛ2[(1 -cos2a)0cos? -sin 2шsiп (6.12)

где /, и /г-действующие значения токов в обмотках; ф - угол сдвига фаз между токами.

Анализ формулы (6.12) показывает, что вращающий момент ферродинамического реле при питании обмоток переменным током имеет как переменную, так и постоянную составляющие. Среднее значение вращающего момента за период Т т

Лвр = fl.p,d/=Vl2C0S?. (6.13)

Таким образом, ферродинамические реле могут работать как на постоянном, так и на переменном токе.

Из (6.13) следует, что ферродинамическая система может использоваться для создания реле сдвига фаз. На ее основе может быть создано также реле мощности, если через одну из обмоток пропускать ток нагрузки, а через другую - ток, пропорциональный приложенному к нагрузке напряжению.

§ 6.2. Индукционные реле

Работа индукционных реле основана на использовании сил взаимодействия переменных магнитных полей неподвижных обмоток с токами, индуктированными этими полями в подвижном электропроводящем элементе. Поэтому такие реле могут работать только на переменном токе. Электропроводящий элемент выполняется в виде диска, цилиндрического ротора, сектора или рамки, имеющих возможность вращения.

Индукционные реле с диском. Упрощенная схема одного из таких реле изображена на рис. 6.4. Реле состоит из шихтованного магиитопровода / с обмоткой 2. Полюсы магиитопровода охватывают алюминиевый диск 5. Ось 4, жестко связанная с диском, может вращаться в подшипнике 3, опираясь нижним концом на подпятник . При отсутствии тока в обмотке подвижный КЭ 6 поджат к упору 8 действием пружины 10 на ось 4. При подаче переменного тока в обмотку диск поворачивается к подвижный КЭ 6 замыкается с неподвижным КЭ 7 - реле срабатывает. Возврат реле осуществляется усилием пружины 10.

Для создания вращающего момента, достаточного для срабатывания индукционного реле, его подвижный электропроводящий элемент должен пронизываться не меиее чем двумя знакомеремеи-ными магнитными потоками, сдвинутыми относительно друг друга в пространстве и во времени (по фазе), что и выполнено в рассматриваемой конструкции с помощью расщепления полюсов на две части К установки на одной из них короткозамкнутых колец 12. В результате в рабочем зазоре магнитной системы образуются магнитные потоки Ф] и Ф2, причем поток Ф\ отстает по фазе от потока Ф2 на угол -ф (рис. 6.5). Эти потоки создают в диске соответствующие трансформаторные ЭДС Ёл и £т2, отстающие от них по фазе На 90° (рис. 6.5). Электродвижущие силы вызывают в диске токи

трансформации In и /т2, которые из-за существования индуктивных составляющих в электрическом сопротивлении диска отстают от ЭДС соответственно на углы уп и (рис. 6.5) *.

С этого места в тексте мы могли бы приступить к объяснению природы появления момента, вращающего диск в рассматриваемой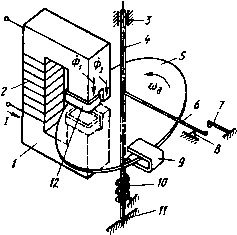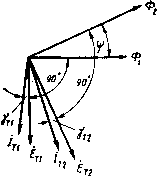

Рис. 6.4. Иидукциоииое реле с диском

Рис. 6.5. Векторная диаграмма индукционного реле

конструкции. Но не будем спешить. Давайте сначала ответим на вопрос: а не создаст ли вращающий момент один магнитный поток?

Согласно закону Ампера, на элементарный участок dl диска с проходящим в нем мгновенным значением тока трансформации при перпендикулярном направлении мгновенного значения Bt вектора магнитной индукции к плоскости диска и синусоидальном характере изменения U и Bt действует переменная во времени элементарная сила

dPt=dlBJ sin О)/• sin (ш/ - 90 - у) = = -d/5„/„ [sin V, -f-cos 90 - у,)]/2.

(6.14)

где Вт и Im - амплитудные значения индукции и тока; <о - угловая частота изменения h и Bt.

* Принимаем, что указанные потоки, ЭДС и токи представляют собой синусоидальные функции времени.

Таким образом, сила,меняется во времени с двойной частотой (рис. 6.6, а-в). Среднее значение этой элементарной силы за период:

(6.15)

dP= J dP,dt=-dlBJ„(sm Vr)/2,

т. е. при ухФО это значение не равно нулю (рис. 6.6, а, б).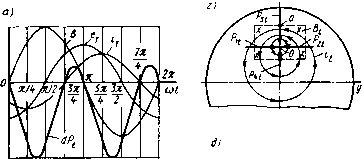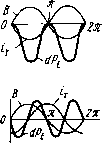

Рис. 6.6. Определение возможности вращения диска индукционной системы под действием одного магнитного потока: а, 6, в -характер нзмеиенин во времени элементарной силы dP соответственно прн T.J -я/4, Я/2 н 0; г - направлення величин B, и P прн нзменении со/ от О до Зя/4 (см. рнс. 6.6, а): а - направлення величин В, н P прн измененнн Ы от ЗЯ/4 до Я; е - четыре варианта расположения полюса электромагнита относительно диска

При уг=п/2 элементарная сила dPt не меняет своего направления в пространстве с течением времени (рис. 6.6,6), а ее среднее значение максимально [см. (6.15)]. При ут=0 сила dPt имеет только переменную составляющую - см. (6.14) и рис. 6.6, в.

Обратимся теперь к рис. 6.6, г, д, на которых изображены часть контура диска и след от одного прямоугольного полюса электромагнита переменного тока, причем центр полюса смещен по оси х относительно центра диска. На этих рисунках за положительное направление Bt принято от нас к диску, а положительное направление it -по правилу правоходового винта (по часовой стрелке). Рис. 6.6, г соответствует изменению ti>t на рис. 6.6, а от О до Зл/4, а рис. 6.6, д - от Зл/4 до л.

На рис. 6.6, г, д также показаны определяемые по правилу левой руки четыре вектора интегральных [по / - см. (6.14)] сил, приведенных по осям у (силы P\t и Pit) и х (силы Рз< и Рц) к точке О схода градиентных линий электрического поля в диске (не показаны на рисунках), перпендикулярных линиям тока 1т. Точка схода О из-за асимметрии полюса относительно оси у смещена от его центра по оси х в сторону центра диска. Из-за симметрии относительно оси X имеем P\t=Pit.

Число линий тока /т в пределах части следа полюса, расположенной на рис. 6.6, г выше плоскости, проходящей параллельно оси у через точку О, больше числа линий тока в пределах остальной части следа полюса, поэтому Рц>Ра1.

На рис. 6.6, д качественное соотношение сил остается прежним (Р„ = Р2,; Рз1>Р4(), но каждая из сил имеет противоположное направление. Как следует из рис. 6.6, а, средние за период от 0*=0 до ш = Зл/4 значения сил больше средних значений сил за период от (1)=Зл/4 до (о=л. Следовательно, среднее значение силы Pst больше среднего значения силы Pt (Рз>4).

Таким образом, мы пришли к выводу, что на диск по оси х действует результирующая сила (Рз<-Pit) с частотой 2о), причем ее среднее значение не равно нулю при ут¥=0 и направлено на выталкивание диска из-под полюса. Последнее определяет физический смысл знака минус в формуле (6.15): сила направлена в сторону снижения токов трансформации при постоянном значении магнитной индукции. Выталкивание диска из-под полюса имеет и энергетическую трактовку: при удаленном диске меньше потребление энергии из сети, так как влияние диска на электромагнитную систему эквивалентно влиянию КЗ витка (см. § 2.3).

К знаку минус в формуле для среднего значения результирующей силы мы придем также, если сравним результаты нашего анализа по направлению силы с рис. 6.6, д, соответствующему принятым положительным направлениям Bt и it. На этом рисунке результирующая сила (Рз<-Р4/) направлена в сторону втягивания диска под полюс.

Мы доказали, что при ут¥=0 иа диск будет действовать среднее значение силы. Однако в случаях, изображенных на рис. 6.6, г, д, диск вращаться не будет, так как направление результирующей силы проходит через его ось (нет плеча). Вращения не будет при любом симметричном расположении полюса относительно радиуса диска (см. позиции /- / на рис. 6.6, е). Но если расположить пря-

моугольный полюс, как показано иа позиции IV рис. 6.6, е, то мгновенное значение вращающего момента Л1вр<#0, а при утФО имеем и среднее значение МврфО.

При промышленной частоте питания обмотки индуктивное электрическое сопротивление диска существенно меньше его активного сопротивления, угол ут мал, мал и вращающий момент, поэтому однополюсные системы ие используются в индукционных реле.

Вернемся теперь к конструкции, изображенной на рис. 6.4. Для упрощения анализа действующих в ней моментов примем сначала на диаграмме рис. 6.5 yti=0 и ут2 = 0. С учетом этого на рис. 6.7 дано изменение во времени мгновенных значений пото- fzi

ков и трансформируемых ими токов при отставании

потока Oi от потока Фг на угол ij)=30°. На рис. 6.8 показаны направления мгновенных значений магнитных потоков Фи и Ф2< двух полюсов (изображены пунктиром), имеющих одинаковые размеры и расположенных симметрично относительно оси у диска, а также токов 1"т1 и 1т2 в диске за один полупериод через промежутки, равные 30°.

При анализе используем метод суперпозиции: изображая линии тока ir\, считаем, что имеется только поток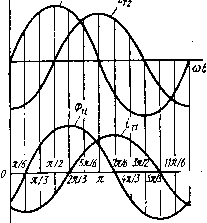

2Л o)t

Рис. 6.7. Измеиение во времени потоков и токов трансформации индукционного реле

Ф,, а изображение линий тока 1т2 связываем с существованием только потока Фг. Положительное направление магнитных потоков считаем от нас к диску, а положительное направление токов - по часовой стрелке.

При (1)=0 (рис. 6.8, а) значение Фг<=0, а ток /тг достиг своего максимального отрицательного значения (см. рис. 6.7), так как перед этим моментом поток Фг< был направлен на нас и уменьшался по модулю. Поток Фи к этому моменту прошел уже свой максимум в отрицательном направлении, но не достиг нулевого значения (рис. 6.7), поэтому ток Iti имеет отрицательное направление, но еще не достиг своего максимального значения. Поток Фи, как мы выяснили ранее, не может создать вращающий момент при Vti = 0, взаимодействуя с током /ть Но взаимодействуя с током /тг, этот поток создает момент вращения MBpi2< = Pi2/ai, направление которого (определяется правилом левой руки) - против часовой стрел-