жении якоря здесь, как ранее было принято в § 5.2, Рц - внешняя сила, равная по значению и противоположная по направлению механической силе Pxi, т. е. Рц=Рца.г. На рис. 5.7,6 штриховой стрелкой для примера показана Ркх\ п. В состоянии I положения / сила Рс\ 1=Рмх11=0.

Кроме сил Pel и Poi, на подвижную часть реле в положении / (рнс. 5.7, а, 6) действует еще сила Pri давления неподвижной контакт-детали на подвижную и сила Р i растянутой противодействующей пружины ПП. Все эти силы показаны иа рис. 5.7, а, б сплошными стрелками. На подвижную часть реле действует также сила реакции центра Ц поворота якоря, не показанная на рис. 5.7, а, б.

Если в положении / убрать неподвижную контакт-деталь, то по направлению К подвижная контакт-деталь пройдет путь /i, равный перемещению конца пружины под действием силы Рки При этом контактная пружина займет положение, показанное на рис. 5.7, а штрихпунктирной линией.

Для работы механизма реле рис. 5.7 кроме положения / характерными являются еще два положения: положение 2 при зазоре 6=62 (рис. 5.7,0), при котором контактное нажатие Рк2 = 0, н положение 3 при притянутом якоре. В положении 2 происходит размыкание контакта при срабатывании реле и замыкание при возврате, контактная пружина находится в свободном состоянии. В положении 3 при 6=63 контакт-детали КД находятся друг от друга на максимальном расстоянии, равном раствору контакта. На рис. 5.7, г для этого конечного положения показаны силы, действующие на якорь в состоянии I, при котором Рез 1/б=Рпзп-

При дальнейшем увеличении внешней силы, действующей на якорь на плече If, по направлению к сердечнику, возникнет сила Рези давления сердечника на якорь, при которой Рбз11в=Рпзп ~Ь -ЬРсзп/б. Силы в состоянии И положения 3 на рис. 5.7 не показаны.

Для упрощения будем полагать, что в каждом из трех положений системы контактная пружина в свободном состоянии параллельна нижней поверхности якоря и что все силы действуют по направлениям К, П, О, перпендикулярным этой поверхности. Вместе с якорем все силы поворачиваются на угол, равный углу поворота якоря.

Механическая характеристика рассматриваемого реле показана на рис. 5.7, d (жирная ломаная li-/ц-2-3i-3u). На участке hi-2 характеристики на подвижную часть реле действуют обе пружины. При этом конктактная пружина создает момент, встречный моменту, создаваемому противодействующей пружиной. На участке 2-3 на подвижную часть реле со стороны механизма действует только сила противодействующей пружины. На рис. 5.7, д характеристика противодействующей пружины - прямая /п-2-5и контактной - прямая /к-2к. Основная часть [In-2-3\) механической характеристики реле получается путем алгебраического

суммирования характеристик противодействующей и контактной пружин.

Формулы для расчета сил и перемещений. В любом из положений, показанных на рис. 5.7, а-г, подвижная часть реле находится в равновесии, поэтому алгебраическая сумма моментов всех сил, действующих на нее относительно любой точки, равна нулю. Относительно точки Ц для состояния I положения 1

Pki/кц - Ят/п + Роп/о = 0.

(5.8)

Здесь и далее положительными приняты моменты, поворачивающие подвижную часть реле относительно точки Ц против часовой стрелки. В этом положении и состоянии Pmxi i = 0. В состоянии II положения 1 (рис. 5.7, 6)

PKUKn+PiiiA-Pmh=0.

(5.9)

Из этого уравнения Pei ii = Pninkiku/e=ni -Якь где m и к1 - силы противодействующей и контактной пружин в положении /, приведенные к /j. Далее все приведенные к U силы будем обозначать со штрихом.

Из (5.8) и (5.9) Pel 11=Ро11/о/б=Ро11. Таким образом, Рмх. 11=Рв. .. = Ро. i = Pm -Рки

В положении 2 (рис. 5.7,0) Рв2/б-Рпгп =0. откуда Рмх2 = =Рв2 = Рп2п/«=п2« Аналогично для состояния I положения 3 (рис. 5.7,2) Рмхз . = Рвз 1=Рпзп /и=Рт-

Для состояния II положения 3: Р. ii = Р 11 = Pl /Ц- -Рсз11 = Рпз-сзп.

Значения сил Poi ь Pki и Рщ показаны на рис. 5.7, д.

При перемещении от положения 1 до положения 2 рабочий зазор изменяется на 612=61-б2=/1/в кц. где f,=Pi/cn; Ск - жесткость контактной пружины, определяется по (5.3) при /=/к (рис. 5.7, а).

При перемещении от положения 2 до положения 3 рабочий зазор изменится на 623 = 62-бз=/п2з/вЛп. где перемещение верхнего конца противодействующей пружины /п2з = АРп зз/сп ; изменение силы противодействующей пружины ДРп2з=пз -Рп2." Сп - жесткость противодействующей пружины.

Устойчивость реле к линейным ускорениям. Устойчивость электротехнического изделия к воздействию механических факторов - его способность нормально функционировать во время их воздействия (ГОСТ 16962-71). Реле можно считать устойчивым к линейным ускорениям, если при этих ускорениях не происходит уменьшения контактного нажатия или раствора контакта, самопроизвольного замыкания и размыкания контакта.

Если реле рис. 5.7, а будет перемещаться с ускорением а вверх в направлении, параллельном векторам сил, то на центр М массы т подвижных частей реле будет действовать сила инерции Рм = -та, направленная вниз (штриховая стрелка Рм на рис. 5.7, о).

в этом случае уравнение равновесия моментов сил в состоянии I положения / (при Pmxi i = 0):

Pki/ku - Pni/п + PouJo + Ямм=О, (5.10)

где Poi la - сила давления якоря на ограничитель ОЯ при наличии ускорения (Poi i в (5.8) - аналогичная сила при отсутствии ускорения).

Наличие или отсутствие ускорения а не может изменить значения сил Рк1 и Рп\, если якорь неподвижен. Из (5.8) и (5.10)

Яо11 в=Poi i - Рмм о=Яо11 - та1к/1о. (5.11)

Таким образом, сила Ро\ ю давления якоря на упор зависит от значения ускорения а. При а-О сила Poi i a=Poi г, при некотором критическом ускорении акр1=Рмкр1/т сила давления якоря на упор Poi 1а = 0. Тогда из (5.11) ускорение Окр! = Poi io/("/m). Так как Poi [lo - Puxt tik, то

aKpI = uiUlV("m).

(5.12)

На рис. 5.7, д штриховой линией / 1-2кр 5кр показана механическая характеристика реле при а„р,. Так как при всех aapi не произошло уменьшения контактного нажатия, реле рис. 5.7, а можно считать устойчивым к линейным ускорениям вплоть до Окр!.

При некотором акр2 подвижная часть реле будет находиться в положении 2, при котором контактное нажатие Рк2=0. Для этого ускорения акр2т/м-Рп2п = 0. откуда акр2 = Рп2п/("м)-

Наконец, при аакрз==Рпзп/("м) якорь силой инерции будет прижат к сердечнику, между контакт-деталями реле установится расстояние, равное раствору контакта.

Таким образом, для повышения устойчивости реле к линейным ускорениям, а значит, и устойчивости к вибрациям и ударам, необходимо увеличивать силу давления якоря на упор в начальном положении системы. Иными словами, необходимо поднимать механическую характеристику, особенно ее точку /ц. Из (5.12) ускорение Дкр! не будет достигнуто при любом Рми п, если сделать /м==0, поэтому самый простой путь повышения рассматриваемой устойчивости - совмещение центра массы подвижных частей реле с центром их поворота, что и сделано в конструкциях реле с уравновешенным якорем (см. рис. 4.2).

ГЛАВА 6. МАГНИТОЭЛЕКТРИЧЕСКИЕ, ЭЛЕКТРОДИНАМИЧЕСКИЕ, ФЕРРОДИНАМИЧЕСКИЕ И ИНДУКЦИОННЫЕ РЕЛЕ

Принцип действия всех этих реле основан на взаимодействии магнитных полей с токами, подведенными к реле извне, или с токами, индуктированными в нем.

§ 6.1. Магнитоэлектрические,

электродинамические

и ферродинамические реле

Магиитоэлектрическое реле - это электромеханическое реле, работа которого основана на взаимодействии магнитного поля постоянного магнита с током в обмотке, подведенным извне.

На рис. 6.1, а схематично изображена одна из конструкций такого реле. Его магнитная система состоит из постоянных магнитов 1 п 3, сердечника 2 и ярма 4. В рабочих зазорах б вращается рамка 5 с намотанной на ней обмоткой. Ток к обмотке от внешнего ис-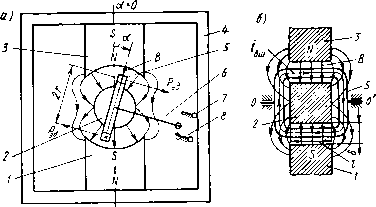

Рис. 6.1. Принципиальная схема магнитоэлектрического реле

точника подводится по спиральным проводам (не показаны на рис. 6.1), которые служат также возвратными пружинами. При отсутствии тока в обмотке они создают момент, удерживающий подвижный контактный элемент (КЭ) 6 замкнутым с неподвижным КЭ 7.

При допущении равномерности магнитного поля в рабочих зазорах с учетом закона Ампера следует, что вращающий момент, действующий на обмотку, определяется выражением

M,,=2rP,=2rlwBi,, (6.1)

где г, I, W - средний радиус, активная длина и число витков обмотки в рабочем зазоре соответственно; В - составляющая магнитной индукции, направленная по радиусу г; iam - ток в обмотке от внешнего источника; Рэд - электродинамическая сила, действующая на активную длину обмотки (рис. 6.1).

Магнитная индукция В, строго говоря, зависит от угла перемещения рамки а (рис. 6.2, а), что следует из анализа распределения Линий магнитной индукции, показанных на рис. 6.1. Соответственно от угла а зависит н вращающий момент. Однако при малых от-

клонениях рамки от вертикального положения (от -Ор до -f-Cp на рис. 6.2, с) можно принять B=const и считать, что

.Р=*и9вш. (6.2)

где k„g=2rlwB.

Из (6.2) следует, что магнитоэлектрические реле могут работать только на постоянном токе.

Предположим, что при токе 1вш, равном значению трогания (вш.тр), движение рамки начинается с а=0 (рис. 6.1). Тогда выражение для механического противодействующего момента спиральных токо-проводящих пружин имеет вид

(6.3)

где с - жесткость пружин; ао - угол, соответствующий их предварительному растяжению от а =-ао до угла трогания атр=0, что необходимо для создания силы контактного нажатия между КЭ 6 и 7 при отсутствии тока 1вш (рис. 6.1).

Пренебрегая трением в подшипниках осей вращения О и О рамки (рис. 6.1, б) и провалом контактов, для статического режима перемещения рамки получим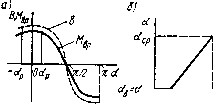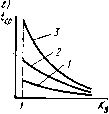

Рис. 6.2. Некоторые характеристики магнитоэлектрического реле:

а - зависимости магнитной индукции В и вращающего момента Л1 от угла а при i-const; б - зависимость угла статического поворота рамки от изменения тока в обмотке; в - кривые динамического изменения угла поворота рамки при трех режимах работы реле: / - колебательном, 2 - критическом, 3 - апериодическом: г - зависимости времени срабатывания реле от коэффициента запаса по току срабатывания (нумерация кривых соответствует рис. 6.2, в)

.Р=-/«х-

(6.4)

Знак минус в (6.3) и (6.4) показывает, что направление Л1вр противоположно положительному направлению Л1вр. Из (6.2) -(6.4) в пределах перемещения рамки:

« = *мэ<-ао. (6.5)

что иллюстрируется рис. 6.2, б, на котором значения аср и 1вш.ср соответствуют срабатыванию реле (замыкание КЭ 6 и 5 при увеличении тока в рамке), а значения ав и Гвш.в - возврату реле (замыкание КЭ 6 и 7 при уменьшении тока).

В динамическом режиме помимо Мвр и Л1„х на рамку действуют успокаивающие тормозные моменты, обусловленные токами,

индуктируемыми в витках обмотки и в рамке (если последняя выполнена из металла), вихревыми токами в толще проводника обмотки, а также трением о воздух.

Электродвижущая сила, индуктируемая в витках обмотки при ее движении в магнитном поле постоянных магнитов, определяется выражением

e„=-d¥/d (6.6)

Если пренебречь размерами поперечного сечения рамки с обмоткой и длиной рабочего зазора б по сравнению со средним радиусом г обмотки (рис. 6.1), принять, что линии индукции в рабочих зазорах перпендикулярны поверхности сердечника и что Вф ф1(а), то потокосцепление W можно рассчитать по формуле

W=2rlwBa. (6.7)

Из (6.6) и (6.7) при В=const получаем

h=-*-,(da/d/).

Ток в обмотке, обусловленный этой ЭДС при допущении чисто активного характера цепи,

i.=eJ(R+R,J=-k„,(Ri-R,J-H(ialdi), (6.8)

где /? -сопротивление обмотки; /?вш - сопротивление внешней цепи с учетом сопротивления источника.

Успокаивающий момент, обусловленный током in, можно найти, используя формулу (6.2):

у.об= -*«а (+-?вш)- (da/dO= -*у.„б (da/dO. (6.9)

где ку.об=к\э/ {R+Явш) - коэффициент успокоения рамки от действия тока, индуктированного в обмотке.

Поскольку моменты от токов, индуктированных в металлической рамке, от вихревых токов, индуктированных в толще проводника обмотки, и момент, обусловленный трением о воздух, также пропорциональны da/d/, то действие всех успокаивающих моментов можно характеризовать величиной [-feyi(da/d/)], где kyz - суммарный коэффициент успокоения рамки.

Таким образом, для динамического режима работы можно записать

*«эвш - J (d Vd2) (da/dO -с (a -fao)=0, (6.10)

где У - момент инерции рамки с обмоткой.

Анализ этого выражения [6] показывает, что в зависимости от значения коэффициента kyz реле может работать в трех режимах, нлмюстрируемых кривыми a=f{t) на рис. 6.2,0: колебательном (кривая /), критическом (кривая 2) и апериодическом (кривая 3). На рис. 6.2,0 ауст обозначает установившееся значение угла а после успокоения рамки в случае удаленного КЭ 8 (см. рис. 6.1), а

- время трогания.