пружины необходимо приложить внешнюю силу, которая возрастает не от нуля, как в случае свободной пружины, а от Р\ (если начало координат - точку 0\ на рис. 5.1, б - расположить у левого конца предварительно сжатой пружины). При дальнейшем сжатии предварительно сжатая пружина ведет себя, как свободная,-сила, создаваемая пружиной, линейно увеличивается до Рмхг при перемещении /2.

Если на рис. 5.1,6 начало координат расположить в точке О пересечения продолжения механической характеристики с осью перемещений, то из сравнения рис. 5.1, а, б видно, что характеристи-

Рнхг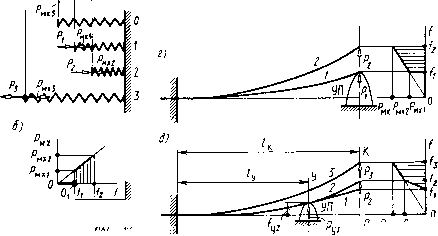

mx miml

Рис. 5.1. Пружины и их механические характеристики

ка предварительно сжатой пружины - это часть характеристики свободной пружины. На участке от точки О до О, (рис. 5.1,6) внешняя сила, необходимая для сжатия предварительно сжатой пружины, равна нулю (механическая характеристика совпадает с осью абсцисс).

Плоская консольная п р у ж и и а (рис. 5.1, в, г, С)-упругая балка с заделанным концом. Работает на изгиб. Поперечное сечение этой пружины показано на рис. 5.1, в в масштабе, увеличенном по сравнению с масштабом, в котором изображена длина пружины I. «Плоской» такая пружина называется потому, что для устойчивости при изгибе ширина b поперечного сечения пружины делается в несколько раз больше высоты h.

Плоские консольные пружины широко распространены в электромагнитных реле в основном в качестве контактных пружин. Такие контактные пружины не только обеспечивают необходимое контактное нажатие, но и несут на себе контакт-детали. Кроме этого, они являются элементами токоведущего контура. Далее будут рассматриваться только плоские консольные контактные пружины. Они используются в реле в двух конструктивных вариантах: в первом контактные пружины консольно закреплены на корпусе (закрепленный конец пружины неподвижен относительно неподвижной части реле - рис. 3.1, 4.1, 6 и § 5.2), во втором контактные пружины консольно закреплены на якоре реле -место их консольного закрепления перемещается вместе с якорем, рис. 4.1, а и § 5.3.

На рис. 5.1, в-d и всех последующих рисунках плоских консольных пружин будут показаны только внешние силы, приложенные к пружинам (эти силы обозначаются без индекса «мх»); механические характеристики будут изображаться для сил, создаваемых пружинами (такие силы обозначаются с индексом «мх»). Консольные пружины в свободном состоянии на этих и на последующих рисунках гл. 5 показаны штрихпунктирной линией.

На рис. 5.1, в-д изображены механические характеристики пружин, на которых f-перемещение правого конца пружины. На рис. 5.1, в пружина изгибается от свободного состояния, на рис. 5.1,г, d -от предварительно изогнутого состояния (7), которое обеспечивается упором пружины УП, расположенным в конце пружины (рис. 5.1, г) и в средней части пружины (рис. 5.1, d). В последнем случае в положении /, когда внешняя сила в конце пружины Pi = 0, со стороны упора пружины УП на нее действует внешняя сила Ру1=фО. Для снятия такой пружины с упора на конце пружины необходимо приложить внешнюю силу, которая от положения / до положения 2 возрастает от нуля до Р2 на некотором перемещении /2-fl. В положении 2 сила давления пружины на упор Ру2 = 0. При изгибе от положения 2 до положения 3 внешняя сила возрастает от Р2 до Рз.

В механизмах электромагнитных реле, использующих консольно закрепленные пружины, перемещения обычно значительно меньше длины пружин (на порядок и более). Для удобства обозначения сил и перемещений на рис. 5.1, в-д и всех последующих рисунках гл. 5 масштаб по оси перемещений сделан существенно больше масштаба, в котором изображена длина пружины. При этом пружина в разных положениях на рисунке условно показана так, что каждая ее точка перемещается при изгибе по направлению действия силы (по вертикали на рис. 5.1,0-d). Направление действия силы принимается всегда перпендикулярным положению пружины в свободном состоянии и не зависящим от того, в каком положении мы рассматриваем изогнутую пружину. Так как длина пружины при изгибе не меняется, в действительности траектория перемещения точек пружины отличается от принятой на рисунках гл. 5. Из-за незначительности перемещений по сравнению с длиной пружин

этим отличием можно пренебречь и пользоваться для расчета прямых консольных пружин формулами теории изгиба упругой балки, полученными при тех же допущениях и известными из курса сопротивления материалов.

Здесь и далее в гл. 5 прописными буквами русского алфавита У (рис. 5.1,(9), К (рис. 5.1,д) и Т, О. П, не использованными на рис. 5.1, обозначены направления, перпендикулярные положению консольной пружины в свободном состоянии. Направление У проходит через точку, в которой пружины опираются иа упор УП, а направление К - через точку приложения внешних сил в конце пружины.

Основным параметром, характеризующим любую пружину, можно считать ее жесткость c=P/f=PMx/f. Здесь Р -внешняя сила; / - перемещение, вызванное этой силой; P„i -сила, развиваемая пружиной (P=P„j). Для пружин на рис. 5.1, а, в жесткость

- мх1 /l - Pux2lf2 - {Р Ui2 - P Mxl)/(/2 -/l)-

(5.1)

Для пружин на рис. 5.1,6, г, д при перемещениях от О до fi жесткость Ci = 0; для пружин на рис. 5.1,6, г при перемещениях от /i до 2 жесткость определяется по (5.1). Для пружины рис. 5.1, d при изгибе в диапазоне перемещений от fi до /г жесткость С2 - = Рмх2/{f2-fi); при изгибе в диапазоне перемещений от /г до /з

жесткость Сз= (/мхз-Рмх2)/(/з-/2).

Жесткость пружины пропорциональна тангенсу угла наклона механической характеристики, которая представляет собой прямую или ломаную линию. Рис. 5.1, (Э показывает, что для изображенной на нем пружины с2>сз>с, = 0. Для предварительно сжатой пружины рис. 5.1,6 и предварительно изогнутой пружины рис. 5.1,г при /, жесткость теоретически равна бесконечности, так как сила возрастает у этих пружин на конечную величину при нулевом перемещении.

Формулы для расчета плоских консольных пружин известны из теории изгиба упругой консольно закрепленной балки. Перемещение любой точки такой балки, измеренное от ее свободного положения до любого г-го,

(5.2)

Если определяется перемещение балки по тому направлению, в котором приложена сила, то в формулу подставляется жесткость пружины, рассчитанная для этого направления:

c = 3EJ/l\

(5.3)

Здесь £~ модуль упругости материала пружины, / - расстояние точки приложения силы (и направления, по которому определяется перемещение) от места заделки балки.

Момент инерции прямоугольного поперечного сечения У=Ш/12, (5.4)

где b и h - ширина и высота поперечного сечения балки.

Если ищется перемещение балки по другому перпендикулярному балке направлению, то в формулу подставляется взаимная жесткость, рассчитанная между направлением приложения силы и направлением, в котором определяется перемещение:

сук=ску =2£У/[/у (/к-/у/3)1, (5.5)

где /у и /к - расстояния направлений У и К до места заделки пружины (рис. 5.1,(3). Всегда берется /к>у независимо от того, в каком из направлений приложена сила и для какого ищется перемещение.

С помощью взаимной жесткости можно определить перемещение правого конца пружины рис. 5.1, д под действием силы Ру1 давления упора на нее f = = Pyi/cy к и перемещение пружины по направлению У под действием приложенной по направлению К силы Р2, которая снимает пружину с упора: f У2 = Р2/сук- Это перемещение равно расстоянию от свободного положения пружины до точки, в которой она опирается на упор УП на рис. 5.1, (3.

В механизмах контактных систем из плоских консольно закрепленных пружин часто на одну пружину действуют две силы в разных точках. На рис. 5.2 вертикальные направления, по которым действуют внешние силы Рк и Рт, обозначены соответственно буквами К н Т. На рис. 5.2, с показана пружина, на которую действует только Рк; на рис. 5.2, 6- только Рт. Обе пружины повторены тонкими линиями (соответственно / и ) на рис. 5.2, в. На последнем жирной линией (кривая Я/) показана пружина, которая находится под воздействием сил Рк и Рт одновременно. Перемещение любой точки этой пружины в диапазоне упругих деформаций может быть найдено алгебраическим суммированием перемещения /рк, созданного силой Рк, и перемещения /рт, созданного силой Рт. Положительными примем перемещения вверх от свободно-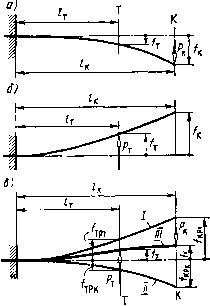

Рис. 5.2. Изгиб плоской консольной пружины при приложении внешней силы в конце пружины (а), в средней части пружины (б), одновременно в конце и средней части (в)

го состояния пружины, отрицательными - вниз. Для иаправлеиия К перемещение fK=fKPT-крк", для направления Т перемещение

§ 5.2. Механизмы реле с плоскими

контактными пружинами,

консольно закрепленными на корпусе

Механизм замыкающего контакта. Электромагнитное реле с замыкающим контактом при максимальном рабочем зазоре - положение /, или начальное,- показано на рис. 5.3, а. Обе плоские контактные пружины, верхняя В и нижняя Я, в этом положении имеют предварительный изгиб: верхняя опирается на упор УП, нижняя - иа толкатель якоря ТЯ. Якорь электромагнита упирается в ограничитель хода якоря ОЯ. Если убрать упор УП и толкатель ТЯ, то пружины Я и В в свободном состоянии займут горизонтальное положение, обозначенное штрихпунктирными линиями. Предварительный изгиб нижней пружины делается для улучшения вибро- и удароустойчнвостн реле, а также устойчивости его к линейным ускорениям (см. § 5.3). Предварительный изгиб пружины В уменьшает дребезг контакта при срабатывании.

На рис. 5.3, а буквами Pyi и Рп показаны силы давления соответственно упора пружины УП и толкателя якоря ТЯ на пружины в положении /. Буквой У показано направление, проходящее через точку, в которой пружина В опирается на упор УП, буквой К - направление, проходящее через точку, в которой контакт-детали КД соприкасаются друг с другом при замкнутом состоянии контакта; буквой Т - направление, проходящее через точку, в которой толкатель якоря ТЯ соприкасается с пружиной Я. Считаем, что силы Pyi всегда направлены по вертикали У, силы Рте - по вертикали Т, силы Pki -по вертикали К независимо от того, какое i-e положение изогнутых пружин рассматривается.

Под механической характеристикой электромагнитных реле в тл. 5 будем иметь в виду зависимость создаваемой механизмом реле суммарной силы Рмх<, приведенной к рабочему зазору, от длины этого зазора б{. Иными словами, механическая сила Рмх< - это та сила, которую можно уравновесить относительно центра Ц поворота якоря внешней силой Рщ (рис. 5.3, а), приложенной к якорю на том же плече te,. Для любого положения якоря Рв1=Рмц. Таким образом, расчет механической характеристики реле рис. 5.3, а заключается в определении зависимости Рщ от bi. Рассмотрим расчет Рд, для наиболее характерных положений якоря. В формулах далее будут использоваться моменты сил только относительно центра Ц поворота якоря.

В положении 1 якорь электромагнита может находиться в двух крайних состояниях: I и II (рис. 5.3,6 и в соответственно). В состоянии I момент силы Pti давления пружины Я на якорь уравно-

вешнвается моментом силы Рои давления ограничителя якоря

(РТ1ТЦ=Р011?0). При этом Рб11 = Рм1Ч=0.

Показатель состояния (I или II) добавляется к индексам сил, в которых обозначаются направление действия силы и положение механизма, только в том случае, если эти силы зависят не только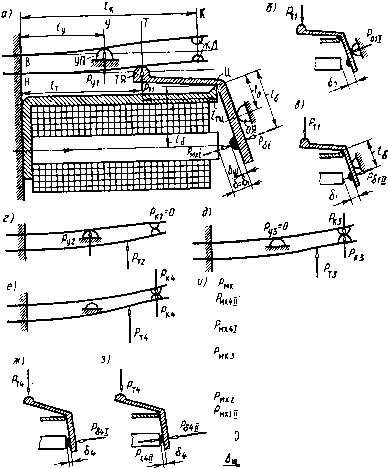

Рис. 5.3. Замыкающий контакт

от положения, но и от состояния. Так как сила, с которой толкатель якоря ТЯ действует на пружину Я, равна силе, с которой пружина Я давит на толкатель, то обе эти силы обозначены одинаково. Так как эти силы зависят только от изгиба пружин, то в состояниях I н II положения / они одинаковы по значению, поэтому в индексе обозначения этой силы отсутствует обозначение состояния.