провода и зазоров, если под векторами Ом.мх на рис. 2.11, а или Омх на рис. 2.13, д, ж иметь в виду магнитное напряжение на суммарном реактивном, а под векторами Um.mr или Ukr - на суммарном активном сопротивлении МЦ;

4) магнитные цепи II и III групп табл. 2.1 отнесены к первому классу условно, так как действие магнитопровода МС этих групп эквивалентно действию вторичной обмотки, замкнутой на активное сопротивление. С другой стороны, заменой МДС вторичной обмотки 2 на реактивное магнитное сопротивление Хма мы можем формально МЦ с двумя МДС (рис. 2.13, г), которые имеются у МС второго класса, привести к МЦ с одной МДС (рис. 2.13, е), которые имеются у МС первого класса (см. классификацию в § 2.1);

5) потери в магнитопроводе эквивалентны по своему действию потерям в короткозамкнутой витке, охватывающем все поперечное сечение магнитопровода, если активная мощность, выделяемая в этом витке, равна потерям в магнитопроводе. На этом основан вывод формулы для расчета удельного реактивного магнитного сопротивления pmjc по удельным потерям в магнитопроводе.

Из (2.43) и (2.53) при Х„.м=Хм2 и 2=1 получим

p„x=Jr„25 =(u) ?2)5 .

Сопротивление эквивалентного КЗВ связано с напряжением (/г на нем и мощностью потерь в нем формулой /?2=f2V2- Потери в эквивалентном КЗВ равны потерям в рассматриваемом магнитопроводе Р2=рга yiS, где ргд -удельные потери на единицу массы магнитопровода; у - плотность материала магнитопровода. С учетом

Ф=адК2

по (2.47) при W2= 1 имеем

Из приведенных уравнений легко получить рмх=2ргд у/(соВт) =

= РГД уЫВт).

Короткозамкнутый виток охватывает часть поперечного сечения полюса (с КЗВ сцеплена только часть потока, сцепленного с обмоткой). На рис. 2.14, а изображена клапанная МС с таким КЗВ (2= = 1). Она рассматривается при притянутом якоре, так как влияние КЗВ сказывается только при малых зазорах. На рис. 2.14, б она повторена с указанием принятых положительных направлений величин (пропорции искажены для удобства обозначений). Сначала рассмотрим эту МС при согласном направлении МДС обмотки и КЗВ.

Основные соотношения. Магнитный поток системы

ф, = Фо+Ф„ (2.54)

где поток Фо проходит через зазор бо и часть полюса шириной Оо и длиной h (рис. 2.14, б), не охваченную КЗВ, а поток Фг -через за-

зор б2 и часть полюса шириной Оа и длиной Л, охваченную КЗВ. На рис. 2.14, б принято 60=62. Поток Ф1 проходит через зазор 61 и все остальные части магнитопровода, кроме участков полюса шириной Оо, 02 и длиной h. На рис. 2.14, б он условно показан двумя линиями индукции.

Схема замещения МЦ приведена на рис. 2.14, в. МДС f2-l2W2= = /2 включена в схему замещения согласно потоку Фг, который сцеплен с КЗВ, потому что они образуют (рис. 2.14, б) правовинто-

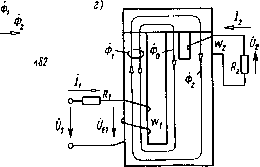Рис. 2.14. Магнитная система с короткозамкнутым витком, охватывающим часть поперечного сечения полюса

вую систему. На схеме замещения приняты следующие обозначения: /?мв1, мбо и/?мб2 -магнитные сопротивления зазоров 6i, 6о и 62; 2м.л<1 = /?м.ж1 + Дм.ж1 -комплексное магнитное сопротивление основной части магнитопровода, в которую входят якорь, ярмо и сердечник на всей длине за вычетом Л; /?м.жо -активное магнитное сопротивление участка полюса длиной Л, шириной Оо и глубиной Ь. Реактивное магнитное сопротивление этого участка не учитывается для упрощения расчетов. Ниже будет показано, что введение КЗВ, охватывающего часть поперечного сечения полюса, приводит к перераспределению потока между зазорами 6о и 62. В результате

увеличения потока Фо индукция в не охваченной КЗВ части полюса становится больше, чем в охваченной: неохваченная часть полюса часто насыщается. Поэтому в схему замещения на пути потока Фо введено магнитное сопротивление участка полюса длиной Л, а на пути потока Фг сопротивление аналогичного участка полюса не учитывается.

По второму закону Кирхгофа, для контура обхода mnpqm <рис. 2.14, б, в) можно написать

Здесь

(2.55)

(2.56)

(2.57)

Подставив

в (2.55), получим

О-Р-и,. (2.58)

По второму закону Кирхгофа для контура обхода mqcdem (рис. 2.14, б), можно определить МДС обмотки Р:

f/„o+m,i + m..i=A, (2.59)

где 7мб1=Ф1/?мб1; 0„.Mi=C[)iZ„.Mi.

На рис. 2.14, г приведена условная схема электрических соединений исходной МС, на которой выделены в виде отдельных элементов активные сопротивления обмоток Ri и R2. Эта схема аналогична схеме рис. 2.13, а, поэтому для цепи обмотки Wi справедлива схема замещения рис. 2.13, б и (2.46) с заменой Ф на Ф а для цепи КЗВ - схема на рис. 2.13, в и (2.47) с заменой Ф иа Фг.

Исследуем влияние КЗВ на потокораспределение рассматриваемой МС. Для этого сравним две одинаковые МС, обмотки которых питаются от источников напряжения Ui и t , при которых в этих -обмотках наводятся ЭДС £i=£i. У первой МС имеется КЗВ (рис. 2.14), а у второй его нет (рис. 2.15).

Сравнение МС с КЗВ сМС без КЗВ. Потоки Ф, и Ф/ обеих систем, протекающие во всех сечениях магиитопровода, кроме участка полюса длиной Л, связаны с ЭДС первичных обмоток по формулам £1=/(ййУ1Ф1 и Ei=j(>iWi<i>i. Так как Ei=Ei, угловая частота ю и число витков обмотки Wi сравниваемых систем одинаковы, то можно считать потоки в их магнитопроводах тоже одинаковыми (Ф1=Ф1). При заданных условиях поток не зависит от наличия или отсутствия КЗВ. Сравнение будем проводить в диапазоне индукций в магнитопроводе, при которых комплексное сопротивление Zm.m 1 магиитопровода можно считать не зависящим от индукции (однаковым в обеих сравниваемых системах).

По рис. 2.15

Ф1 = Фо + Ф2,

(2.60)

где Фо и Фг - потоки, проходящие через левую и правую части полюса соответственно. Фазы всех этих потоков совпадают, так как магнитные сопротивления на их пути имеют одинаковый характер (активные) и к ветвям этих потоков приложено одинаковое на-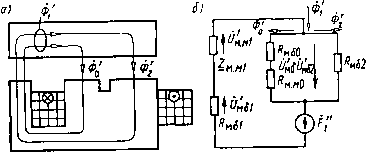

Рис. 2.15. Магнитная система рис. 2.14 со снятым короткозамк-нутым витком

пряжение /мо=Ьмв2. Если на часть полюса МС рис. 2.15, а надеть КЗВ и провести небольшую коррекцию напряжения питания, заключающуюся в сохранении неизменным ЭДС обмотки, то в ней к потокам, изображенным на рис. 2.15, добавится поток Фкзв , показанный на рис. 2.16. Этот поток создает в а) МС рис. 2.14 МДС F2 = =l2W2 = h. Так как Фкзв на своем пути встречает только активные магнитные сопротивления, то фаза его совпадает с фазой

Выше было доказано, что у МС рис. 2.15, а и 2.14, а, б потоки Ф1 в магнитопроводе одинаковы. Это означает, что в МС рис. 2.14, а, б КЗВ не может создать поток, пронизывающий обмотку w\ и замыкающийся по магнипопроводу по пути npcden (рис. 2.14,6), поэтому на рис. 2.16, а, б такой поток не показан.

Потоки в зазорах бо и бг МС рис. 2.14 найдем суммированием потоков, показанных на схемах рис. 2.15 и 2.16:

(2.61) 65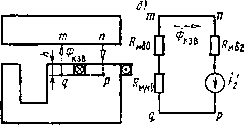

Рис. 2.16. Магнитная система рнс. 2.14 с потоком Фкзв , создаваемым в ней коротко-замкнутым витком

Фо=Фо-Фкзв; Ф2 = Ф2+ФКЗВ.

На рис. 2.17, а по полученным уравнениям построены две векторные диаграммы: сплошными стрелками - для МС с КЗВ. штрихпунктирными стрелками с одной точкой - для МС без КЗВ. Штрихпунктирными стрелками с двумя точками показан поток Фкзв, создаваемый КЗВ в системе рис. 2.14.

Векторная диаграмма МС с КЗВ. По действительной оси отложен поток Фг. ЭДС £г, наводимая в КЗВ, отстает от него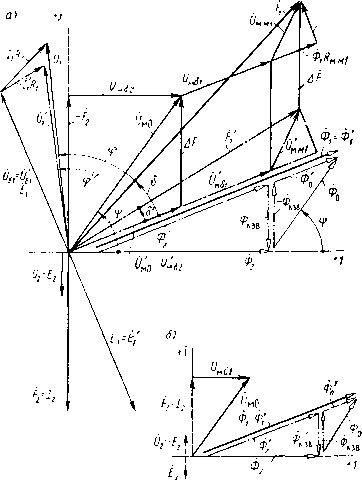

Рис. 2.17. Векторные диаграммы

на 90°. Напряжение t/г на активном сопротивлении КЗВ равно Ё2 [см. (2.47) J. С (Уг=/гг совпадает по направлению МДС КЗВ £г= = /2. От конца вектора -F2 параллельно вектору Фг откладываем вектор бмвг магнитного напряжения на зазоре 62, так как Фг и 66

Смва имеют одинаковую фазу [см. (2.56)]. Замыкает треугольник магнитных напряжений вектор Омо, который состоит из векторов Оммо И Омю [см. (2.57)]. Так как при принятом допущении Umo= =Фомо. где /?мо=м.жо+м*о. то вектор От параллелен вектору Фо. Последний откладываем вдоль полученного направления от конца вектора Фг. Замыкающим треугольник потоков будет вектор Ф1 [см. (2.54)]. Параллельно вектору Ф1 от конца векторов Омо и Омб2 откладываем магнитные напряжения /мб1 = Ф1мб1 и <i)i/?M.«i, перпендикулярно - вектор /Ф1ХМ.Л.1. Замыкающим будет вектор МДС обмотки Pi-liWi [см. (2.59)]. ЭДС £i в обмотке отстает от

потока Ф1 на 90°. Составляющая Ое\ напряжения питания Ои компенсирующая Е\, равна по величине и противоположно направлена этой ЭДС (при согласном направлении МДС). Вектор t\R\ параллелен вектору МДС обмотки /i = /i(Oi. Треугольник электрических напряжений строим по (2.45).

Попутно заметим, что магнитное напряжение 7мо между точками m и <jr (или п н р) схемы рис. 2.14, в мы можем разложить на активную и реактивную составляющие: /мо=мл2+/мхг=млг+ + iUf,iX2- Из векторной диаграммы рис. 2.17, а видно, что 17млг= Ом(,2 = Ф2Рм(,2 и ОмХ2=-р2- Эти урзвнения соответствуют замене КЗВ в схеме замещения МЦ (см. рис. 2.14, в) не МДС Р2, а реактивным магнитным сопротивлением Хи2, магнитное напряжение на

котором ОмХ2 = 1ФХм2-

Векторная диаграмма МС без КЗВ (см. рис.2.15). Поток Ф/ этой системы, сцепленный с витками обмотки Wu при принятом условии равенства ЭДС £i МС с КЗВ и МС без КЗВ остается равным потоку Ф1 системы с КЗВ. Так как поток Фкзв замыкается по зазорам бо и 62, а также по участку полюса длиной Л, сопротивление которого носит активный характер (см. рис. 2.16, б), то поток Фкзв совпадает по фазе с МДС КЗВ Fz-h-Этот поток мы получим на диаграмме рис. 2.17, а, если из конца вектора Фг восставим перпендикуляр до пересечения с вектором Ф1. Треугольник потоков Фь Фо и Фг, соответствующий (2.54), разбивается на два треугольника, соответствующих (2.61), а вектор Ф1=Ф1 - на две составляющие Фг и Фо, соответствующие (2.60) и совпадающие по направлению.

МДС МС без КЗВ по рис. 2.15, б

Г[=и:+иш + и:..г. (2.62)

Магнитное напряжение 7мо=мб2 (см. рис. 2.15, б) откладываем на рис. 2.17, а вдоль векторов Фо, Фг и Ф/ (заметим, что

\0мо\<\Оио\, так как Фо<Фо и (/мо=Фо-мо; /мо=Фомо. К концу вектора Омо добавляем вектор 0мб1 напряжения на зазоре 6i и вектор 0м,м) напряжения на сопротивлении Zm.*i основной