11.2. Принцип неопределенности

Движение частицы можно описать на классическом языке, используя ее координаты и импульс. Можно предсказать будущее состояние частицы, основываясь на детерминистских законах динамики. В квантовой механике ситуация иная. Здесь невозможно определить одновременно две наблюдаемые величины, такие, как момент р и координату х частицы с точностью, лучшей, чем следует из принципа неопределенности Гейзенбер-га. Согласно этому принципу, если Др и Дл; - неопределенности в измерениях величин р и х, то

ДрАл; > ft/4jt. (11.2)

Неопределенность в переменной z, изображаемая символом Az, может быть представлена как среднеквадратичное отклонение от среднего значения переменной, найденное из серии измере-

ний, т.е. Az - сокращенное обозначение среднего у bz, где б2 - отклонение от среднего в единичном измерении. Пары величин, которые подчиняются принципу неопределенности, известны как сопряженные переменные. Примером другой сопряженной пары могут служить энергия системы Е и время t, в течение которого она обладает этой энергией. Неопределенность для этих величин выражается неравенством

AEAth/4n. (11.3)

Хотя принцип неопределенности описывает квантовомехани-ческое явление, он имеет классический аналог [4], который может дать интуитивное представление о написанных выше неравенствах. Рассмотрим гармонический сигнал с угловой частотой (Оо, который ограничен интервалом (-Г/2, Г/2) так, чтобы получился импульс x{t), изображенный на рис. 11.1,с. Предположим, что этот импульс был получен в результате измерения и что мы хотим определить время прибытия и частоту гармонического сигнала.

квантовомеханический принцип без ограничений на модели или системы, к которым он применяется. Поэтому можно использовать принцип неопределенности, чтобы доказать с наиболее общей точки зрения, что существует фундаментальный, квантовомеханический нижний предел для шумов, которыми может обладать линейный усилитель. Так оно и есть на самом деле. Аргументы в пользу этого положения представлены в разд. 11.3 сразу после предварительного обсуждения самого принципа неопределенности, приведенного ниже.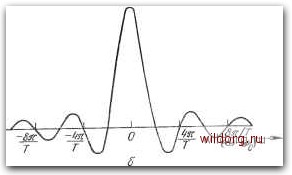

Рис. 11.1.

а - гармонический сигнал, ограниченный интервалом {-TI2, Т/2); б - преобразование Фурье.

Если

X {t) = cos при I I < т/2.

О в остальных случаях,

то фурье-преобразованием x{t) является функция г/2

{М = \ cos ехр -jwtdt =

-г/2

sin [(со - соо) т/2] i sin [((О + щ) Т/2] (со-СОо) (ш + Шо)

(11.4)

(11.5)

Для круговых частот вблизи значения шо второй член в правой части выражения (11.5) пренебрежимо мал и функция Х(/а)) хорошо аппроксимируется выражением

sin[(co -соо)Г/2]

(со - СОо)

Х(/ш) = -

(11.6)

график которого представлен на рис. 11.1,6 как функция от аргумента (ю-Ио). Кривая обладает главным максимумом при co=tuo, показывая, что основные спектральные компоненты сигнала группируются вокруг частоты гармонической волны. Однако пик имеет конечную ширину, делающую невозможным точ-

ное определение частоты гармонического сигнала. Иными словами, ширина пика создает неопределенность в измерении частоты.

Мерой неопределенности является полуширина пика До) между первыми двумя нулями по обе стороны от значения соо

Дсй = 2я/Г. (11.7)

Поскольку величина Асо обратно пропорциональна длительности импульса Т, то «размывание» по частоте уменьшается при увеличении времени наблюдения. Однако длительность импульса устанавливает меру неопределенности во времени его прибытия, которое можно уменьшить, если пожертвовать информацией о частоте. Очевидно, что уравнение (11.7) является формой соотношения неопределенности, которое имеет место независимо от каких-либо квантовомеханических представлений. Однако его можно выразить в тех же самых переменных, что и уравнение (11.3), если ввести постоянную Планка и сформулировать неопределенности в виде

AE = hAw/2n, At = T, (11.8)

где АЕ и А - неопределенности энергии и времени прибытия. В результате комбинации этих условий с уравнением (11.7) получаем соотношение

AEAt = h, (11.9)

которое, очевидно, согласуется с неравенством в принципе неопределенности Гейзенберга.

!1.3. Квантовьгй предел для шума усилителя

Электромагнитное излучение проявляет дуализм в своем поведении, оказываясь по характеру то корпускулярным (как в фотоэлектрическом эффекте), то волноподобным (как в явлениях интерференции). Смысловой аспект этого «раздвоения», наблюдаемого на практике, целиком зависит от проводимого эксперимента. Вообще говоря, было бы значительно проще списывать все эксперименты, связанные с электромагнитным излучением исключительно либо с корпускулярной, либо с волновой точки зрения, однако это невозможно. Необходимость использования дуального представления является общепризнанной.

Корпускулярное описание поля было предложено Эйнштейном [2], который ввел кванты энергии (или фотоны) электромагнитного поля. Согласно Эйнштейну, общая энергия Е поля