C = C/{G+G-G). (9.18)

Таким образом, щирина полосы

Б = ((02-cui)/2n= 1/2лС = (G-fG,-G)/23xC, (9.19)

ш произведение корня !Квадратного из коэффициента усиления «а щирину полосы имеет вид

Б1/П = /СДузгС. (9.20)

Произведение коэффициента усиления на ширину полосы в выражении (9.20) является полезной величиной, характеризующей усилитель. Она подтверждает наше прежнее заявление о том, ЧТО емкость С должна быть как можно меньше. Очевидно, чем больше значения, принимаемые Gs и Gl, тем больше произведение коэффициента усиления на ширину полосы. Это означает, что усилитель должен иметь высокий коэффициент усиления и что (Gs + Gl) должно быть приблизительно (но не точно) равно G. Из этого условия находим, что максимальное произведение коэффициента усиления на ширину полосы равно

(5]/о)п1ахО/2яС, (9.21)

ЧТО имеет место, когда Gs=Gl = G/2. Эта симметрия между проводимостями источника и нагрузки, необходимая для достижения оптимального условия (9.21), несовместима, однако, с другими аспектами поведения туннельного диода. В частности, она не соответствует условию достижения минимального коэффициента шума, как мы покажем ниже.

9.4.3. Коэффициент шума усилителя

на туннельном диоде . . , ... ...... . -

Когда вычисляется коэффициент шума туннельного диода, необходимо рассматривать два шумовых генератора: генератор напряжения Vn{t), представляющий тепловой шум, обусловленный сопротивлением объемных областей, и генератор тока in{t), представляющий дробовой шум в туннельных токах. Эти генераторы показаны на эквивалентной схеме усилителя на тун-

Ширину ПОЛОСЫ усилителя на уровне половинной мощности находят из выражения (9.15). Если угловые частоты на верхнем и нижнем уровнях половинной мощности равны ог и coi соответственно, то

нельном диоде на рис. 9.5,а. Генератор тока ins{t) представляет шум, связанный с источником.

Для вычисления коэффициента шума удобно преобразовать по Нортону эквивалентную схему туннельного диода, как показано на рис. 9.5,6. Здесь последовательный генератор напряжения Vn{t) и параллельный генератор тока in{t) преобразованы

ins (О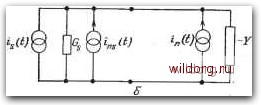

Рис. 9.5. Эквивалентная схема усилителя на туннельном диоде с генераторами шума (а) и эквивалентная схема Нортона (б).

В параллельный генератор тока ii{t), а полная проводимость -У имеет вид

-Y =

(R-Rb)

(9.22)

где 1(0с/2я=/с---частота отсечки туннельного диода, задаваемая формулой (9.12).

Спектральные плотности шумовых генераторов тока in{t) й напряжения v„(t) описываются формулами

(9.23а)

(9.236)

где шум, связанный только с туннельным током, приближенно принят за чисто дробовой шум. Для рабочей точки в области отрицательного сопротивления вольт-амперной характеристики

ЭТО оправдано, так как приложенное напряжение несколька больше, чем 2kQlq, и функция котангенса в выражениях (9.8) и (9.9) очень близка к единице. Проводимость Ge в формуле (9.23а) представляет собой проводимость теплового шума, эквивалентную дробовому шуму в туннельном токе. Из формул-(9.23) и рис. 9.5 следует, что когда Vn(t) и in (О некоррелированны, спектральная плотность генератора тока i\{t) на рис. 9.5, б определяется формулой

5,(и) =

V R-Rb I

Sv («) + Si (ш)

(R-Rb)

to" / Rb \ (Oc [R-Rbj

(9.24>

Считая, что этот генератор находится при той же температуре, что и туннельный диод, получаем спектральную плотность генератора шумового тока

5~И = 4Ш,. (9.25>

Теперь из рис. 9 5,6 можно просто записать коэффициент шума усилителя в виде

Si (со)

( Rb ) (йс \ R - Rbl

GsiR-RbY

Rb \

-Rb I

(9.26a)

Для низких частот (ниже частоты отсечки) это выражение переходит в выражение

~ Gs(R-RbY GsiR-НьГ

(0<(0,.

(9.266)

Из выражения (9.266) очевидно, что, для того чтобы коэффициент шума был минимальным, проводимость источника должна быть как можно :больше. Мы видели, что в усилителе на туннельном диоде с высоким коэффициентом усиления

Gs+G G, (9-27)

хотя равенство в этом выражении исключается, если усилитель должен оставаться устойчивым. Согласно соотношению (9.27), максимальное значение

-"smax

(9.28)

что приводит выражение для низкочастотного коэффициента шума к виду

(9.29)